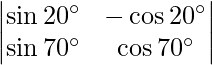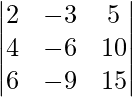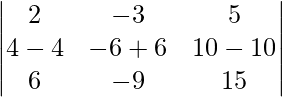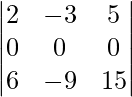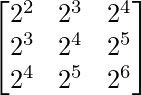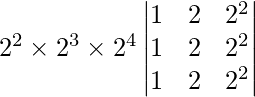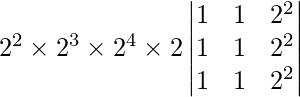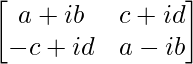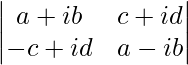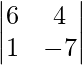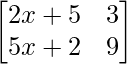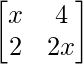Clase 12 RD Sharma Solutions – Capítulo 6 Determinantes Ejercicio Ej. 6.6 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 19. Sea A = [a ij ] una array cuadrada de orden 3 × 3 y C ij denote el cofactor de a ij en A. Si |A| = 5, encuentra el valor de a 11 C 21 + a 12 C 22 + a 13 C 23 .

Solución:

Como sabemos que, si una array es una array cuadrada de orden n, entonces la suma de los productos de los elementos de una fila o una columna con los cofactores de los elementos correspondientes de alguna otra fila o columna es cero. 

Asi que, 

A = [a ij ] es una array cuadrada de orden n.

También tenemos,

\sum^n_{j = 1} a_{ij} C_{kj} = 0

Y \sum^n_{i = 1} a_{ij} C_{ik} = 0

=> un 11 C 21 + un 12 C 22 + un 13 C 23 = 0 

Por lo tanto, el valor requerido es 0.

Pregunta 20. Encuentra el valor de 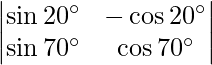 \begin{vmatrix}\sin 20^\circ & - \cos 20^\circ\\ \sin 70^\circ& \cos 70^\circ\end{vmatrix}.

Solución:

Dado que, 

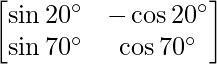
un = \begin{bmatrix} \sin 20^\circ & - \cos 20^\circ\\\sin 70^\circ & \cos 70^\circ \end{bmatrix} 

=> |A| = \begin{vmatrix} \sin 20^\circ & - \cos 20^\circ\\\sin 70^\circ & \cos 70^\circ \end{vmatrix}

= sen 20° cos 70° + cos 20° sen 70°

= pecado (20° + 70°)

= pecado 90

= 1

Pregunta 21. Si A es una array cuadrada que satisface A T A = I, escribe el valor de |A|.

Solución:

Supongamos que A = [a ij ] sea una array cuadrada de orden n.

Entonces, usando la propiedad de los determinantes, obtenemos

=> |A| = |A T |

Aquí tenemos

=> UNA T UNA = yo

=> |A T A| = 1

Entonces, los determinantes son del mismo orden, obtenemos

=> |A T A| = |A T | |A|

=> |A T | |A| = 1

=> \izquierda| Un \derecho| = \frac{1}{\izquierda| A^T \derecho|}

=> \izquierda| Un \derecho| = \frac{1}{\izquierda| Un \derecho|}

=> |A| 2 = 1

=> |A| = ±1

Por lo tanto, el valor de |A| es ±1.

Pregunta 22. Si A y B son arrays cuadradas del mismo orden tales que |A| = 3 y AB = I, luego escribe el valor de |B|.

Solución:

Según la pregunta, A y B son arrays cuadradas del mismo orden.

Entonces, usando la propiedad de los determinantes obtenemos,

=> |AB| = |A| |B|

Aquí, |A| = 3, AB = yo.

=> |AB| = 1

=> |A| |B| = 1

=> 3 |B| = 1

=> |B| = 1/3

Por lo tanto, el valor de |B| es 1/3.

Pregunta 23. A es un sesgo simétrico de orden 3, escribe el valor de |A|.

Solución:

Aquí, |A| = 4.

Entonces tenemos,

Orden de la array (n) = 3

Usando las propiedades de las arrays, obtenemos

Para una array cuadrada de orden n y constante k, sabemos,

=> |kA| = k norte | A |

=> |- A| = (-1) 3 |A|

= (-1) (4)

= -4

Por lo tanto, el valor de |A| es -4.

Pregunta 24. Si A es una array cuadrada de orden 3 con determinante 4, entonces escribe el valor de |−A|.

Solución:

Dado que, |A| = 4.

Orden de la array (n) = 3

Entonces, usando las propiedades de las arrays, obtenemos

=> |kA| = k norte | A |

=> |- A| = (-1) 3 |A|

= (-1) (4)

= -4

Por lo tanto, el valor de |A| es -4.

Pregunta 25. Si A es una array cuadrada tal que |A| = 2, escribe el valor de |AA T |.

Solución:

Dado que, |A| = 2

Como sabemos que en una array cuadrada, |A| = UNA T

Entonces, son de orden cuerdo. 

Por lo tanto, |AA T | = |A| |A T |

=> |AA T | = 2 (2)

= 4

Por lo tanto, el valor de |AA T | es 4

Pregunta 26. Encuentra el valor del determinante  \begin{vmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{vmatrix} .

Solución:

Dado que, 

un = \begin{bmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{bmatrix}

|A| = \begin{vmatrix}243 & 156 & 300 \\ 81 & 52 & 100 \\ - 3 & 0 & 4\end{vmatrix}

Al aplicar R 1 -> R 1 – 3R 2 tenemos,

= \begin{vmatrix} 243 - \left( 81 \times 3 \right) & 156 - \left( 52 \times 3 \right) & 300 - \left( 100 \times 3 \right)\\ 81 & 52 & 100\\ - 3 & 0 & 4 \end{vmatrix}

= \begin{vmatrix} 0 & 0 & 0\\ 81 & 52 & 100\\ - 3 & 0 & 4 \end{vmatrix}   

= 0

Por lo tanto, el valor del determinante es 0.

Pregunta 27. Encuentra el valor del determinante 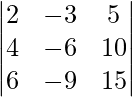 \begin{vmatrix}2 & - 3 & 5 \\ 4 & - 6 & 10 \\ 6 & - 9 & 15\end{vmatrix} .

Solución:

Dado que, 

un = \begin{bmatrix}2 & - 3 & 5 \\ 4 & - 6 & 10 \\ 6 & - 9 & 15\end{bmatrix}

|A| = \begin{vmatrix} 2 & - 3 & 5\\4 & - 6 & 10\\6 & - 9 & 15 \end{vmatrix}

Al aplicar R 2 -> R 2 – 2R 1 obtenemos,

= \begin{vmatrix} 2 & - 3 & 5\\4 - 4 & - 6 + 6 & 10 - 10\\6 & - 9 & 15 \end{vmatrix}

= \begin{vmatrix} 2 & - 3 & 5\\0 & 0 & 0\\6 & - 9 & 15 \end{vmatrix}

= 0

Por lo tanto, el valor del determinante es 0.

Pregunta 28. Si la array 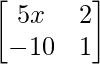 \begin{bmatrix}5x & 2 \\ - 10 & 1\end{bmatrix}  es singular, encuentra el valor de x.

Solución:

Como sabemos que una array es singular solo cuando su determinante es cero. 

Según la pregunta, 

\begin{bmatrix}5x & 2 \\ - 10 & 1\end{bmatrix}  es una array singular

Asi que, 

=> |A| =  \begin{vmatrix} 5x & 2 \\- 10 & 1 \end{vmatrix}  = 0

Al expandir el determinante obtenemos,

=> 5x + 20 = 0 

=> x = -20/5

=> x = -4

Por lo tanto, el valor de x es -4.

Pregunta 29. Si A es una array cuadrada de orden n × n tal que |A| = λ, luego escribe el valor de |−A|.

Solución:

Dado que,

A es una array cuadrada de orden n × n

Entonces, |A| = λ

=> |- A| = (-1) n A

=> |-A| = (-1) norte λ

Por lo tanto, el valor de |-A| es (-1) n λ.

Pregunta 30. Encuentra el valor del determinante 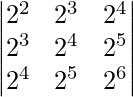 \begin{vmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{vmatrix} .

Solución:

Dado que, 

un = \begin{bmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{bmatrix}

|A| = \begin{vmatrix}2^2 & 2^3 & 2^4 \\ 2^3 & 2^4 & 2^5 \\ 2^4 & 2^5 & 2^6\end{vmatrix}  

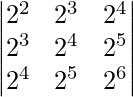
Al sacar factores comunes de R 1 , R 2 y R 3 obtenemos,

= 2^2 \times 2^3 \times 2^4 \begin{vmatrix} 1 & 2 & 2^2 \\1 & 2 & 2^2 \\1 & 2 & 2^2 \end{vmatrix}

Aquí, las dos filas son idénticas, por lo que obtenemos

= 2^2 \times 2^3 \times 2^4 \times 2 \begin{vmatrix} 1 & 1 & 2^2 \\1 & 1 & 2^2 \\1 & 1 & 2^2 \end{vmatrix}

= 0 

Por lo tanto, el valor del determinante es 0.

Pregunta 31. Si A y B son arrays no singulares del mismo orden, prueba si AB es singular o no singular.

Solución:

Según la pregunta, A y B sean arrays no singulares de orden n.  

Aquí, |A| ≠ 0 y |B| ≠ 0. 

Entonces, el orden de estas arrays es el mismo, obtenemos

=> |AB| = |A| |B|

=> |AB| = 0 si |A| = 0 o |B| = 0

Pero como no es el caso aquí, entonces |AB| es array distinta de cero y AB es array no singular.

Por lo tanto probado.

Pregunta 32. Una array de orden 3 × 3 tiene determinante 2. ¿Cuál es el valor de |A (3I)|, donde I es la array identidad de orden 3 × 3?

Solución:

Dado que una array de orden 3 x 3 tiene determinante 2. 

Entonces supongamos que B es la array. entonces el orden de la array es 3

y |B| = 2  

Consideremos que I es la array identidad, por lo que obtenemos

=> |yo| = 1 

=> 3 |yo| = 3

=> |A (3I)| = |3A|

= 3 3 |A|

= 27 (2)

= 54

=> |A (3I)| = 54

Por lo tanto, el valor de |A (3I)| es 54

Pregunta 33. Si A y B son arrays cuadradas de orden 3 tales que |A| = −1, |B| = 3, luego encuentra el valor de |3 AB|.

Solución:

Tenemos,

A y B son arrays cuadradas de orden 3.

También |A| = −1, |B| = 3.

Sabemos,

Como n es del orden de A, obtenemos

=> |KA| = Kn | A| 

=> |3AB| = 3 3 |AB|  

Si el orden de las arrays A y B es el mismo y son arrays cuadradas, entonces |AB| = |A| |B|. 

Entonces tenemos,

=> |3AB| = 3 3 |A| |B|

= 27 (-1) (3)

= -81

Por lo tanto, el valor de |3 AB| es -81.

Pregunta 34. Escribe el valor de 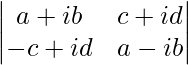 \begin{vmatrix}a + ib & c + id \\ - c + id & a - ib\end{vmatrix} .

Solución:

Tenemos,

un = \begin{bmatrix}a + ib & c + id \\ - c + id & a - ib\end{bmatrix}

|A| = \begin{vmatrix}a + ib & c + id \\ - c + id & a - ib\end{vmatrix}

= a 2 – iab + iab – i 2 b 2 – (-c 2 – icd + icd + i 2 d 2 ) 

= un 2 – yo 2 segundo 2 + c 2 – yo 2 re 2  

Aquí tenemos, i 2 = – 1.

Entonces obtenemos,  

|A| = un 2 – (-1) segundo 2 + c 2 – (-1) re 2  

= un 2 + segundo 2 + c 2 + re 2

Por lo tanto, el valor es a 2 + b 2 + c 2 + d 2 .

Pregunta 35. Escribe el cofactor de un 12 en la siguiente array 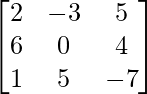 \begin{bmatrix}2 & - 3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & - 7\end{bmatrix} .

Solución:

Tenemos

\begin{bmatrix}2 & - 3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & - 7\end{bmatrix}

Asi que,

=> un 12 = -3

Ahora encontramos el cofactor de un 12 

un 12 = (-1) 1+2 \begin{vmatrix}6 & 4 \\ 1 & - 7\end{vmatrix}

= – (- 42 – 4) 

= 46

Por lo tanto, el valor del cofactor requerido es 46.

Pregunta 36. Si 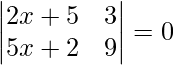 \begin{vmatrix}2x + 5 & 3 \\ 5x + 2 & 9\end{vmatrix} = 0 , encuentra x.

Solución:

Aquí tenemos,

un = \begin{bmatrix}2x + 5 & 3 \\ 5x + 2 & 9\end{bmatrix}

=> |A| =  \begin{vmatrix}2x + 5 & 3 \\ 5x + 2 & 9\end{vmatrix}  = 0

=> 9(2x + 5) – 3(5x + 2) = 0

=> 18x + 45 – 15x – 6 = 0  

=> 3x + 39 = 0

=> 3x = – 39 

=> x = -39/3 

=> x = -13

Por lo tanto, el valor de x es -13.

Pregunta 37. Encuentra el valor de x de lo siguiente: 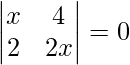\begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix} = 0

Solución:

Tenemos,

un = \begin{bmatrix}x & 4 \\ 2 & 2x\end{bmatrix}

|A| = \begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix} = 0

=>  \begin{vmatrix}x & 4 \\ 2 & 2x\end{vmatrix}  = 0 

=> 2 x 2 – 8 = 0 

=> 2×2 = 8

=> x2 = 8/2

=> x2 =   4

=> x = √4

=> x = ±2

Por lo tanto, el valor de x es ±2.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *