Clase 12 RD Sharma Solutions – Capítulo 28 La línea recta en el espacio – Ejercicio 28.3

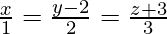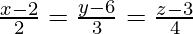Pregunta 1. Muestra que las rectas $\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}$ y se $\frac{x-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}$ intersecan y encuentra su punto de intersección.

Solución:

Dado que las coordenadas de cualquier punto de la primera línea son

$\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}=\lambda$

⇒ x = λ, y = 2λ + 2, z = 3λ – 3

Las coordenadas de un punto general sobre la segunda línea están dadas por:

$\frac{-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}=\mu$

⇒ x = 2 μ + 2, y = 3 μ + 6, z = 4 μ + 3

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

λ – 2μ = 2 ……(1)

2λ – 3μ = 4 ……(2)

3λ – 4μ = 6 …..(3)

Resolviendo este sistema de ecuaciones, obtenemos

λ = 2 y μ = 0

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 3(2) – 4(0)

= 6 = lado derecho

Por lo tanto, las rectas dadas se cortan en (2, 6, 3).

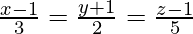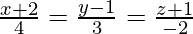Pregunta 2. Demuestra que las rectas $\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}$ y $\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}$ no se intersecan.

Solución:

Dado que las coordenadas de cualquier punto de la primera línea son

$\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}=\lambda$

⇒ x = 3λ + 1, y = 2λ – 1, z = 5λ + 1

Las coordenadas de un punto general sobre la segunda línea están dadas por:

$\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}=\mu$

⇒ x = 4μ – 2, y = 3μ + 1, z = -2μ – 1

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

3λ – 4μ = -3 ……(1)

2λ – 3μ = 2 ……(2)

5λ + 2μ = -2 …..(3)

Resolviendo este sistema de ecuaciones, obtenemos

λ = -17 y μ = -12

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 3(-17) + 2(-12)

= -75 ≠ lado derecho

Por lo tanto, las líneas dadas no se cortan entre sí.

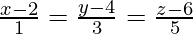Pregunta 3. Muestra que las rectas $\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}$ y se $\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}$ intersecan y encuentra su punto de intersección.

Solución:

Dado que las coordenadas de cualquier punto de la primera línea son

$\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}=\lambda$

⇒ x = 3λ – 1, y = 5λ – 3, z = 7λ – 5

Las coordenadas de un punto general sobre la segunda línea están dadas por:

$\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}=\mu$

⇒ x = 2 μ + 2, y = 3 μ + 6, z = 4 μ + 3

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

3λ – μ = 3 ……(1)

5λ – 3μ = 7 ……(2)

7λ – 5μ = 11 …..(3)

Resolviendo este sistema de ecuaciones, obtenemos

λ = 1/2 y μ = -3/2

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 3(2) – 4(0)

= -3/2 = lado derecho

Ahora pon el valor de λ en la primera ecuación y obtenemos

x = 1/2, y = -1/2, z = -3/2

Por lo tanto, las rectas dadas se cortan en (1/2, -1/2, -3/2).

Pregunta 4. Demuestra que la recta que pasa por (0, -1, -1) y B(4, 5, 1) interseca a la recta que pasa por C(3, 9, 4) y D(-4, 4, 4). Además, encuentre su punto de intersección.

Solución:

Dado que las coordenadas de cualquier punto de la recta AB son

$\frac{x-0}{4-0}=\frac{y+1}{5+1}=\frac{z+1}{1+1}=\lambda$

⇒ x = 4λ, y = 6λ – 1, z = 2λ – 1

Además, dado que las coordenadas de cualquier punto de la línea CD son

$\frac{x-3}{3+4}=\frac{y-9}{9-4}=\frac{z-4}{4-4}=\mu$

⇒ x = 7 μ + 3, y = 5 μ + 9, z = 4

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

4λ – 7μ = 3 ……(1)

6λ – 5μ = 10 ……(2)

λ = 5/2 …..(3)

⇒ λ = 5/2 y μ = 1.

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 4(5/2) – 7(1)

= 3 = lado derecho

Ahora pon el valor de λ en la línea AB, obtenemos

x = 10, y = 14, z = 4

Por tanto, las rectas dadas AB y CD se cortan en el punto (10, 14, 4).

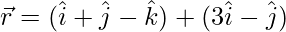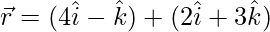Pregunta 5. Demuestra que la recta $\vec{r}=(\hat{i}+\hat{j}-\hat{k})+λ(3\hat{i}-\hat{j})$ y se $\vec{r}=(4\hat{i}-\hat{k})+μ(2\hat{i}+3\hat{k})$ intersecan y encuentra su punto de intersección.

Solución:

Según la pregunta, se da que el vector de posición de dos puntos sobre las rectas es

$\vec{r}=(\hat{i}+\hat{j}-\hat{k})+λ(3\hat{i}-\hat{j})$

$\vec{r}=(4\hat{i}-\hat{k})+μ(2\hat{i}+3\hat{k})$

Si las líneas se cruzan, entonces para algún valor de λ y μ, debemos tener:

$(1+3\lambda)\hat{i}+(1-\lambda)\hat{j}-\hat{k}=(4+2\mu)\hat{i}+0\hat{j}+(3\mu-1)\hat{k}$

Ahora igualamos el coeficiente de $\hat{i}, \hat{j},\hat{k}$ obtenemos

1 + 3λ = 4 + 2μ ……(1)

1 – λ = 0 …..(2)

-1 = -1 +3μ …..(3)

Al resolver la ecuación, obtenemos

λ = 1 y μ = 0.

Ahora, reemplazando los valores en la ecuación (1), obtenemos

1 + 3(1) = 4 + 2(0)

4 = 4

LHS = RHS

Así, las coordenadas del punto de intersección de las dos rectas son (4, 0, -1).

Pregunta 6. Determina si los siguientes pares de rectas se intersecan o no:

(yo) 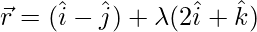$\vec{r}=(\hat{i}-\hat{j})+\lambda( 2\hat{i}+\hat{k})$ y $\vec{r}=(2\hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}-\hat{k}).$

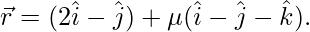
Solución:

Dado que:

$\vec{r}=(\hat{i}-\hat{j})+\lambda( 2\hat{i}+\hat{k})$

$\vec{r}=(2\hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}-\hat{k}).$

Si las líneas se cruzan, entonces para algún valor de λ y μ, debemos tener:

$(1+2\lambda)\hat{i}-\hat{j}+\lambda\hat{k}=(2+\mu)\hat{i}+(-1+\mu)\hat{j}-\mu\hat{k}$

Ahora igualamos el coeficiente de $\hat{i}, \hat{j},\hat{k}$ obtenemos

1 + 2λ = 2 + μ …..(1)

-1 = -1 + µ …..(2)

λ = -μ …..(3)

Al resolver las ecuaciones, obtenemos

λ = 0 y μ = 0.

Ahora, sustituimos los valores en la ecuación (1), obtenemos

1 + 2λ = 2 + μ

1 + 2(0) = 2 + 0

1 ≠ 2

IZQ ≠ DERECHO

Por lo tanto, las rectas dadas no se cortan.

(ii) 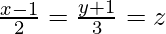$\frac{x-1}{2}=\frac{y+1}{3}=z$ y $\frac{x+1}{5}=\frac{y-2}{1};z=2$

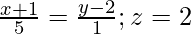
Solución:

Dado que las coordenadas de cualquier punto de la recta AB son

$\frac{x-1}{2}=\frac{y+1}{3}=z=\lambda$

⇒ x = 2λ + 1, y = 3λ – 1, z = λ

Las coordenadas de un punto general en la segunda línea están dadas por

$\frac{x+1}{5}=\frac{y-2}{1}=\mu;z=2$

⇒ x = 5μ – 1, y = μ + 2, z = 2

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

2λ – 5μ = -2 ……(1)

3λ – μ = 3 ……(2)

λ = 2 …..(3)

Resolviendo este sistema de ecuaciones, obtenemos

λ = 2 y μ = 3

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 2(2) – 5(3)

= -2 ≠ lado derecho

Por lo tanto, las líneas dadas no se cortan entre sí.

(iii) 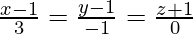$\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}$ y $\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}$

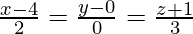
Solución:

Dado que las coordenadas de cualquier punto de la recta AB son

$\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}=\lambda$

⇒ x = λ, y = 2λ + 2, z = 3λ – 3

Las coordenadas de un punto general en la segunda línea están dadas por

$\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}=\mu$

⇒ x = 2μ + 4, y = 0, z = 3μ – 1

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

λ – 2μ = 2 …….(1)

2λ – 3μ = 4 ……(2)

3λ – 4μ = 6 ……(3)

Al resolver este sistema de ecuaciones, obtenemos

λ = 1 y μ = 0

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 3(1) – 2(0)

= 3 = lado derecho

Por lo tanto, las rectas dadas se cortan en (4, 0, -1).

(iv) 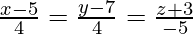$\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}$ y $\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}$

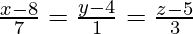
Solución:

Dado que las coordenadas de cualquier punto de la recta AB son

$\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}=\lambda$

⇒ x = 4λ + 5, y = 4λ + 7, z = -5λ – 3

Las coordenadas de un punto general sobre la segunda línea están dadas por:

$\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}=\mu$

⇒ x = 7 μ + 8, y = μ + 4, z = 3 μ + 5

Si las rectas se cortan, para algunos valores de λ y μ, debemos tener:

4λ – 7μ = 3 …….(1)

4λ – μ = -3 ……(2)

5λ + 3μ = -8 ……(3)

Al resolver este sistema de ecuaciones, obtenemos

λ = -1 y μ = -1

Al sustituir los valores en la ecuación (3), tenemos

IZQ = 5(-1) – 3(-1)

= -8 = lado derecho

Por lo tanto, las rectas dadas se cortan en (1, 3, 2).

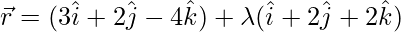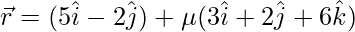Pregunta 7. Demuestra que las rectas $\vec{r}=(3\hat{i}+2\hat{j}-4\hat{k})+\lambda( \hat{i}+2\hat{j}+2\hat{k})$ y $\vec{r}=(5\hat{i}-2\hat{j})+\mu(3\hat{i}+2\hat{j}+6\hat{k})$ se intersecan. Por lo tanto, encuentre su punto de intersección.

Solución:

Dado que,

$\vec{r}=(3\hat{i}+2\hat{j}-4\hat{k})+\lambda( \hat{i}+2\hat{j}+2\hat{k})$

$\vec{r}=(5\hat{i}-2\hat{j})+\mu(3\hat{i}+2\hat{j}+6\hat{k})$

Si las líneas se cruzan, entonces para algún valor de λ y μ, debemos tener:

$(3+\lambda)\hat{i}-\hat{j}+(2+2\lambda)\hat{j}+(2\lambda-4)\hat{k}=(2+\mu)\hat{i}+(-1+\mu)\hat{j}-\mu\hat{k}$

Ahora igualamos el coeficiente de $\hat{i}, \hat{j},\hat{k}$ obtenemos

3 + λ = 5 + 3μ ……..(1)

2 + 2λ = -2 + 2μ ……..(2)

2λ – 4 = 6μ ……..(3)

Resolviendo la ecuación, tenemos:

λ = -4 y μ = -2.

Al sustituir los valores, obtenemos

IZQ = 2(-4) – 4

= -12

lado derecho = 6(-2)

= -12

Por lo tanto, las líneas dadas se cortan en el punto (-1, -6, -12).

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Muestra que las rectas y se intersecan y encuentra su punto de intersección.

Pregunta 2. Demuestra que las rectas y no se intersecan.

Pregunta 3. Muestra que las rectas y se intersecan y encuentra su punto de intersección.

Pregunta 4. Demuestra que la recta que pasa por (0, -1, -1) y B(4, 5, 1) interseca a la recta que pasa por C(3, 9, 4) y D(-4, 4, 4). Además, encuentre su punto de intersección.

Pregunta 5. Demuestra que la recta y se intersecan y encuentra su punto de intersección.

Pregunta 6. Determina si los siguientes pares de rectas se intersecan o no:

(yo) y

(ii) y

(iii) y

(iv) y

Pregunta 7. Demuestra que las rectas y se intersecan. Por lo tanto, encuentre su punto de intersección.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Muestra que las rectas $\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}$ y se $\frac{x-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}$ intersecan y encuentra su punto de intersección.

Pregunta 2. Demuestra que las rectas $\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}$ y $\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}$ no se intersecan.

Pregunta 3. Muestra que las rectas $\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}$ y se $\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}$ intersecan y encuentra su punto de intersección.

Pregunta 5. Demuestra que la recta $\vec{r}=(\hat{i}+\hat{j}-\hat{k})+λ(3\hat{i}-\hat{j})$ y se $\vec{r}=(4\hat{i}-\hat{k})+μ(2\hat{i}+3\hat{k})$ intersecan y encuentra su punto de intersección.

(yo) $\vec{r}=(\hat{i}-\hat{j})+\lambda( 2\hat{i}+\hat{k})$ y $\vec{r}=(2\hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}-\hat{k}).$

(ii) $\frac{x-1}{2}=\frac{y+1}{3}=z$ y $\frac{x+1}{5}=\frac{y-2}{1};z=2$

(iii) $\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}$ y $\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}$

(iv) $\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}$ y $\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}$

Pregunta 7. Demuestra que las rectas $\vec{r}=(3\hat{i}+2\hat{j}-4\hat{k})+\lambda( \hat{i}+2\hat{j}+2\hat{k})$ y $\vec{r}=(5\hat{i}-2\hat{j})+\mu(3\hat{i}+2\hat{j}+6\hat{k})$ se intersecan. Por lo tanto, encuentre su punto de intersección.