En matemáticas, se dice que una array cuadrada es diagonalmente dominante si para cada fila de la array, la magnitud de la entrada diagonal en una fila es mayor o igual que la suma de las magnitudes de todas las demás entradas (no diagonales). en esa fila. Más precisamente, la array A es diagonalmente dominante si

Por ejemplo, la array
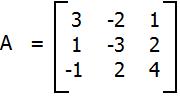
es diagonalmente dominante porque
|a 11 | ≥ |a 12 | + |a 13 | desde |+3| ≥ |-2| + |+1|
|un 22 | ≥ |a 21 | + |a 23 | desde |-3| ≥ |+1| + |+2|
|un 33 | ≥ |a 31 | + |a 32 | desde |+4| ≥ |-1| + |+2|
Dada una array A de n filas y n columnas. La tarea es verificar si la array A es diagonalmente dominante o no.
Ejemplos:
Input : A = { { 3, -2, 1 },
{ 1, -3, 2 },
{ -1, 2, 4 } };
Output : YES
Given matrix is diagonally dominant
because absolute value of every diagonal
element is more than sum of absolute values
of corresponding row.
Input : A = { { -2, 2, 1 },
{ 1, 3, 2 },
{ 1, -2, 0 } };
Output : NO
La idea es ejecutar un ciclo desde i = 0 hasta n-1 para el número de filas y para cada fila, ejecutar un ciclo j = 0 hasta n-1 para encontrar la suma del elemento no diagonal, es decir, i != j. Y verifique si el elemento diagonal es mayor o igual que la suma. Si para alguna fila, es falso, devuelva falso o imprima «No». De lo contrario, escriba «SÍ».
Implementación:
C++
// CPP Program to check whether given matrix
// is Diagonally Dominant Matrix.
#include <bits/stdc++.h>
#define N 3
using namespace std;
// check the given matrix is Diagonally
// Dominant Matrix or not.
bool isDDM(int m[N][N], int n)
{
// for each row
for (int i = 0; i < n; i++)
{
// for each column, finding sum of each row.
int sum = 0;
for (int j = 0; j < n; j++)
sum += abs(m[i][j]);
// removing the diagonal element.
sum -= abs(m[i][i]);
// checking if diagonal element is less
// than sum of non-diagonal element.
if (abs(m[i][i]) < sum)
return false;
}
return true;
}
// Driven Program
int main()
{
int n = 3;
int m[N][N] = { { 3, -2, 1 },
{ 1, -3, 2 },
{ -1, 2, 4 } };
(isDDM(m, n)) ? (cout << "YES") : (cout << "NO");
return 0;
}
Java
// JAVA Program to check whether given matrix
// is Diagonally Dominant Matrix.
import java.util.*;
class GFG {
// check the given matrix is Diagonally
// Dominant Matrix or not.
static boolean isDDM(int m[][], int n)
{
// for each row
for (int i = 0; i < n; i++)
{
// for each column, finding
//sum of each row.
int sum = 0;
for (int j = 0; j < n; j++)
sum += Math.abs(m[i][j]);
// removing the diagonal element.
sum -= Math.abs(m[i][i]);
// checking if diagonal element is less
// than sum of non-diagonal element.
if (Math.abs(m[i][i]) < sum)
return false;
}
return true;
}
/* Driver program to test above function */
public static void main(String[] args)
{
int n = 3;
int m[][] = { { 3, -2, 1 },
{ 1, -3, 2 },
{ -1, 2, 4 } };
if (isDDM(m, n))
System.out.println("YES") ;
else
System.out.println("NO");
}
}
// This code is contributed by Arnav Kr. Mandal.
Python3
# Python Program to check
# whether given matrix is
# Diagonally Dominant Matrix.
# check the given
# matrix is Diagonally
# Dominant Matrix or not.
def isDDM(m, n) :
# for each row
for i in range(0, n) :
# for each column, finding
# sum of each row.
sum = 0
for j in range(0, n) :
sum = sum + abs(m[i][j])
# removing the
# diagonal element.
sum = sum - abs(m[i][i])
# checking if diagonal
# element is less than
# sum of non-diagonal
# element.
if (abs(m[i][i]) < sum) :
return False
return True
# Driver Code
n = 3
m = [[ 3, -2, 1 ],
[ 1, -3, 2 ],
[ -1, 2, 4 ]]
if((isDDM(m, n))) :
print ("YES")
else :
print ("NO")
# This code is contributed by
# Manish Shaw(manishshaw1)
C#
// C# Program to check whether given matrix
// is Diagonally Dominant Matrix.
using System;
class GFG {
// check the given matrix is Diagonally
// Dominant Matrix or not.
static bool isDDM(int [,]m, int n)
{
// for each row
for (int i = 0; i < n; i++)
{
// for each column, finding
//sum of each row.
int sum = 0;
for (int j = 0; j < n; j++)
sum += Math.Abs(m[i, j]);
// removing the diagonal element.
sum -= Math.Abs(m[i, i]);
// checking if diagonal element is less
// than sum of non-diagonal element.
if (Math.Abs(m[i,i]) < sum)
return false;
}
return true;
}
// Driver program
public static void Main()
{
int n = 3;
int [,]m = { { 3, -2, 1 },
{ 1, -3, 2 },
{ -1, 2, 4 } };
if (isDDM(m, n))
Console.WriteLine("YES") ;
else
Console.WriteLine("NO");
}
}
// This code is contributed by Vt_m.
PHP
<?php
// PHP Program to check whether
// given matrix is Diagonally
// Dominant Matrix.
// check the given matrix
// is Diagonally Dominant Matrix or not.
function isDDM( $m, $n)
{
// for each row
for ($i = 0; $i < $n; $i++)
{
// for each column, finding
// sum of each row.
$sum = 0;
for ( $j = 0; $j < $n; $j++)
$sum += abs($m[$i][$j]);
// removing the diagonal element.
$sum -= abs($m[$i][$i]);
// checking if diagonal element
// is less than sum of non-diagonal
// element.
if (abs($m[$i][$i]) < $sum)
return false;
}
return true;
}
// Driver Code
$n = 3;
$m = array(array( 3, -2, 1 ),
array( 1, -3, 2 ),
array( -1, 2, 4 ));
if((isDDM($m, $n)))
echo "YES";
else
echo"NO";
// This code is contributed by SanjuTomar
?>
Javascript
<script>
// JavaScript Program to check whether given matrix
// is Diagonally Dominant Matrix.
// check the given matrix is Diagonally
// Dominant Matrix or not.
function isDDM(m, n)
{
// for each row
for (let i = 0; i < n; i++)
{
// for each column, finding
//sum of each row.
let sum = 0;
for (let j = 0; j < n; j++)
sum += Math.abs(m[i][j]);
// removing the diagonal element.
sum -= Math.abs(m[i][i]);
// checking if diagonal element is less
// than sum of non-diagonal element.
if (Math.abs(m[i][i]) < sum)
return false;
}
return true;
}
// Driver code
let n = 3;
let m = [[ 3, -2, 1 ],
[ 1, -3, 2 ],
[ -1, 2, 4 ]];
if (isDDM(m, n))
document.write("YES") ;
else
document.write("NO");
</script>
YES
Complejidad de Tiempo: O(N 2 )
Espacio Auxiliar: O(1)