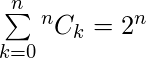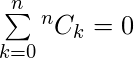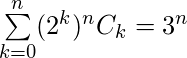La expresión ![]() denota
denota ![]() tiempos. Esto se puede evaluar como la suma de los términos que implican
tiempos. Esto se puede evaluar como la suma de los términos que implican ![]() para k = 0 a n, donde el primer término se puede elegir de n lugares, el segundo término de (n-1) lugares, el
para k = 0 a n, donde el primer término se puede elegir de n lugares, el segundo término de (n-1) lugares, el ![]() término de (n-(k-1)) lugares y así sucesivamente. Esto se expresa como
término de (n-(k-1)) lugares y así sucesivamente. Esto se expresa como 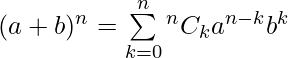 . La expansión binomial usando símbolos combinatorios es
. La expansión binomial usando símbolos combinatorios es
- El grado de cada término
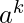 [Tex]b^{nk} [/Tex]en la expansión binomial anterior es del orden n.
[Tex]b^{nk} [/Tex]en la expansión binomial anterior es del orden n. - El número de términos en la expansión es n+1.
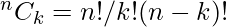 Del mismo modo
Del mismo modo 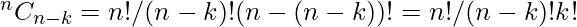 , por lo tanto, se puede concluir que
, por lo tanto, se puede concluir que 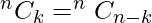 .
.
Sustituyendo a = 1 y b = x en la expansión binomial, para cualquier entero positivo n obtenemos ![]() . Corolario 1:
. Corolario 1:
para cualquier entero no negativo n. Reemplazando x con 1 en la expansión binomial anterior, obtenemos ![]() . Corolario 2:
. Corolario 2:
para cualquier entero positivo n. Reemplazando x con -1 en la expansión binomial anterior, obtenemos ![]() . Corolario 3: Reemplazando x con 2 en la expansión binomial anterior, obtenemos
. Corolario 3: Reemplazando x con 2 en la expansión binomial anterior, obtenemos ![]() En general, se puede decir que
En general, se puede decir que
Además, uno puede combinar el corolario 1 y el corolario 2 para obtener otro resultado, ![]() [Tex]^nC_0 + ^nC_2 + .. = ^nC_1 + ^nC_3 + … [/Tex]Suma de coeficientes de términos pares = Suma de coeficientes de términos impares términos. Dado que
[Tex]^nC_0 + ^nC_2 + .. = ^nC_1 + ^nC_3 + … [/Tex]Suma de coeficientes de términos pares = Suma de coeficientes de términos impares términos. Dado que  , 2(
, 2( ![]() [Tex]^nC_0 + ^nC_2 + .. = 2^{n-1} [/Tex]
[Tex]^nC_0 + ^nC_2 + .. = 2^{n-1} [/Tex]
Contar Los coeficientes de los términos en la expansión ![]() corresponden a los términos del triángulo de pascal en la fila n.
corresponden a los términos del triángulo de pascal en la fila n.
| 1 | 1 | |
Publicación traducida automáticamente
Artículo escrito por Anand_Shekhar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA