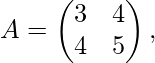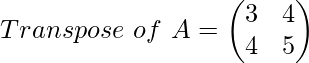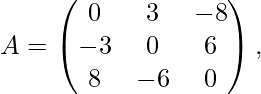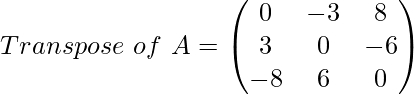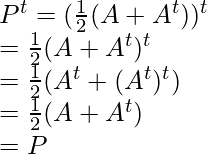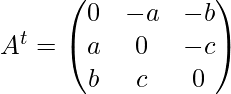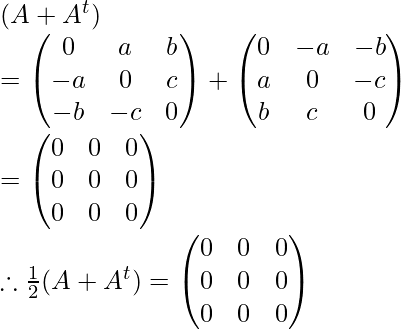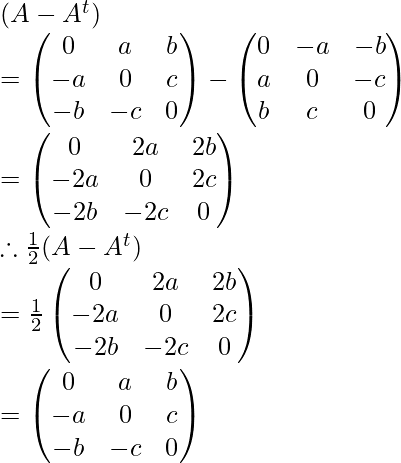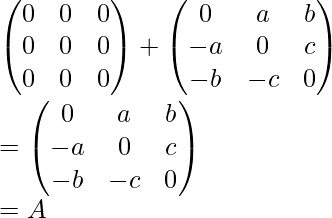El conocimiento de arrays es necesario para diversas ramas de las matemáticas. Las arrays son una de las herramientas más poderosas de las matemáticas. Ahora vea una de las características de la array en este artículo. Aquí discutimos las arrays simétricas y simétricas sesgadas. De acuerdo con las arrays, solo las arrays cuadradas pueden ser de forma simétrica o sesgada. Más adelante en este artículo, discutiremos todas las cosas.
Array simétrica
Si para una array, la forma transpuesta de esa array es la misma que la array original, entonces se dice que esa array es una array simétrica. Sea, se dice que una array cuadrada A de tamaño nxn es simétrica si
Donde, [a ij ] = [a ji ] , para 1 ≤ yo ≤ norte , y 1 ≤ j ≤ norte . En este caso , [a ij ] es un elemento en la posición (i, j) que es la i -ésima fila y la j -ésima columna en la array A, y [a ji ] es un elemento en la posición (j, i) que es la j -ésima fila y i -ésima columna en la array A. Así que es la forma transpuesta de la array A.
Ejemplo
Entonces, esta array es una array simétrica, porque la forma transpuesta de esta array es en sí misma la array original.
Arrays sesgadas simétricas
Si para una array, la forma transpuesta de esa array es la misma que la negativa de la array original, entonces se dice que esa array es una array simétrica oblicua. Sea, se dice que una array cuadrada A de tamaño nxn es asimétrica si
Donde, [a ij ] = [a ji ] , para 1 ≤ yo ≤ norte , y 1 ≤ j ≤ norte . En este caso , [a ij ] es un elemento en la posición (i, j) que es la i -ésima fila y la j -ésima columna en la array A, y [a ji ] es un elemento en la posición (j, i) que es la j -ésima fila y i -ésima columna en la array A.
Ejemplo
Aquí, en la forma transpuesta, la array parece el negativo de la array original.
Propiedades de arrays simétricas y asimétricas
Hay algunas reglas que provienen del concepto de arrays simétricas y simétricas oblicuas,
1. Si la array A es una array cuadrada entonces (A + A t ) siempre es simétrica.
Demostrar:
Para encontrar si una array es simétrica o no, primero tenemos que encontrar la forma transpuesta de la array dada
Entonces, busquemos la transpuesta de (A + A t )
Entonces, esto es lo mismo que la array dada, por lo que es simétrica.
2. Si la array A es una array cuadrada, entonces (A – ) siempre es sesgadamente simétrica.
Demostrar:
Para encontrar si una array es asimétrica o no, primero, tenemos que encontrar la forma transpuesta de la array dada
Entonces, encontremos la transpuesta de (A – )
Entonces, esta forma es el negativo de la array dada, por lo que es sesgadamente simétrica.
Expresión de arrays en forma de arrays simétricas y sesgadas simétricas
Demostrar:
Sea A una array cuadrada,
Podemos escribir, A = A/2 + A/2
Sea, A = P + Q
Ahora, encuentra P t y Q t
y,
Entonces, aquí P es simétrica y Q son arrays asimétricas y A es la suma de P y Q.
Ejemplo
Exprese la array A como la suma de una array simétrica y asimétrica, donde
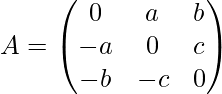
Responder:
Primero, encuentra la transpuesta de A
Ahora encuentra (A + A t ) y (A – A t )
Similarmente:
Ahora, comprueba que la suma de (1/2)(A + A t ) y (1/2)(A – A t ) es igual o no a A,
Así que aquí A se expresa como la suma de la array simétrica y asimétrica.
Publicación traducida automáticamente
Artículo escrito por SoumikMondal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA