Métodos gráficos para resolver pares de ecuaciones lineales en dos variables

un eso,,

vida real

Roman fue a una papelería y compró 2 lápices y 3 gomas de borrar por Rs 9. Su amiga Sonam vio la nueva variedad de lápices y gomas de borrar con Roman, y también compró 4 lápices y 6 gomas de borrar del mismo tipo por Rs 18. Representa esto situación algebraica y gráficamente.

Solución:

Digamos que el costo de un lápiz es Rs.x y el costo de un borrador es Rs. y. Entonces las ecuaciones se pueden formular como,

2x + 3y = 9,

4x + 6y = 18,

Grafiquemos ambos en un gráfico,

Al ponerlos en forma de intersección,

$\frac{2x}{9} + \frac{3y}{9} = 1$

$\frac{4x}{18} + \frac{6y}{18} = 1$

La gráfica de ambas ecuaciones queda de la siguiente manera,

Ambas líneas tienen las mismas ecuaciones y, por lo tanto, coinciden.

Pregunta 2: Un entrenador del equipo de cricket compró 3 bates y 6 pelotas por Rs 3900. Posteriormente, compró otro bate y 3 pelotas más del mismo tipo por Rs 1300. Representa esta situación de forma algebraica y geométrica.

Solución:

Digamos que el costo de cada bate es Rs. «x» y Balls es Rs. «y».

3x + 6y = 3900

x + 3y = 1300

Hagamos gráficas de estas ecuaciones, se puede hacer a través de cualquiera de las formas que se enseñaron, pero nos ceñiremos a la forma de intersección

$\frac{3x}{3900} + \frac{6y}{3900} = 1$

$\frac{x}{1300} + \frac{3y}{1300} = 1$

Ahora las gráficas de ambas ecuaciones resultan ser,

Podemos ver que estas líneas se cruzan en un punto.

Método gráfico de solución

En este método, graficamos ambas ecuaciones y luego tratamos de encontrar las intersecciones. Ahora, al graficar y encontrar las posibles intersecciones, puede haber tres casos que pueden ocurrir

Solución única
Sin solución
Infinidad de soluciones

Solución única

Un par de ecuaciones lineales en dos variables, que tiene una solución, se llama un par consistente de ecuaciones lineales. En tales casos, ambas líneas se cruzan entre sí.

Por ejemplo:

Pregunta 1: Resuelve el par de ecuaciones dado con el método gráfico.

x + 3y = 6

2x – 3y = 12

Solución:

Primero necesitamos graficar ambos para encontrar la solución. Vamos a traerlos en forma de intercepción,

$\frac{x}{6} + \frac{3y}{6} = 1$

$\frac{2x}{12} - \frac{3y}{12} = 1$

Ambas ecuaciones ahora se pueden trazar en el gráfico.

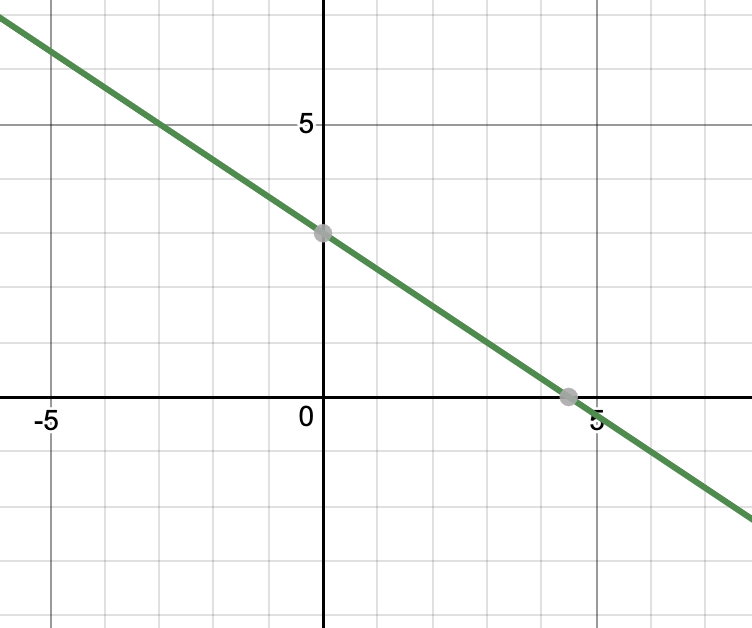
Podemos ver en el gráfico que ambas líneas se cruzan en (6,0), por lo que esta es la solución a este par de ecuaciones lineales.

Pregunta 2: Ragini fue a una tienda a comprar pantalones y faldas. Cuando sus amigas le preguntaron cuántos de cada uno había comprado, ella respondió: “La cantidad de faldas es dos menos que el doble de la cantidad de pantalones comprados. Además, el número de faldas es cuatro menos que cuatro veces el número de pantalones comprados”. Ayuda a sus amigas a encontrar cuántos pantalones y faldas compró Ragini.

Solución:

Digamos que hay un número «x» de pantalones y un número «y» de faldas. Luego se forman las siguientes ecuaciones.

y = 2x – 2

y = 4x – 4

Dibujemos gráficas para ambas ecuaciones,

Del gráfico, podemos ver que estas líneas se cruzan en (1,0). Así que esta es la solución para este sistema de ecuaciones.

x = 1 y y = 0

Eso significa que Ragini trajo 1 pantalón y 0 faldas.

Sin solución

Un par de ecuaciones lineales en dos variables, que no tiene solución, se llama un par inconsistente de ecuaciones lineales. En tales casos, ambas líneas son paralelas, por lo que nunca se cruzan.

Por ejemplo:

Pregunta: Dibuja las ecuaciones lineales en el gráfico para las dos ecuaciones dadas,

7x-9y = 4

7x-9y = 12

Solución:

El gráfico para las dos ecuaciones dadas se verá así,

Como está claro que las líneas no se cortan entre sí en ningún punto, son de naturaleza paralela. Por lo tanto, no hay solución para las ecuaciones lineales dadas.

Infinidad de soluciones

Un par de ecuaciones lineales en dos variables, que tienen infinitas soluciones, se denomina par de ecuaciones lineales dependientes. En tales casos, ambas líneas coinciden entre sí.

Por ejemplo:

Generalicemos los casos anteriores,

un ₁ x + segundo ₁ y + c ₁ = 0

un ₂ x + _{segundo 2} y + c ₂ = 0

Estas ecuaciones son,

Intersección si, $\frac{a_1}{a_2} \ne \frac{b_1}{b_2}$
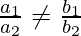
Coincidente si, $\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$
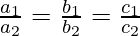
Paralelo si, $\frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2}$

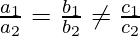
Pregunta: Dibuja las ecuaciones lineales en el gráfico, también encuentra la solución para las dos ecuaciones lineales.

8x+13y = 17

16x+26y = 34

Solución:

Las dos ecuaciones no solo son paralelas, sino que se superponen, por lo tanto, todos los puntos se intersecan entre sí. Por lo tanto, existen infinitas soluciones para las ecuaciones lineales dadas.

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Método gráfico de solución

Solución única

Sin solución

Infinidad de soluciones

Deja una respuesta Cancelar la respuesta