El método de eliminación gaussiana también se conoce como método de reducción de filas y es un algoritmo que se utiliza para resolver un sistema de ecuaciones lineales. Suele entenderse como una secuencia de operaciones realizadas sobre la correspondiente array de coeficientes. Este algoritmo se utiliza para encontrar:
- El rango de una array.
- El determinante de una array.
- La inversa de una array.
Las operaciones que podemos realizar sobre la array a modificar son:
- Intercambio/intercambio de dos filas.
- Multiplicar o dividir una fila por un número entero positivo.
- Sumar o restar un múltiplo de una fila a otra.
Ahora usando estas operaciones podemos modificar una array y encontrar su inversa. Los pasos involucrados son:
- Paso 1: Crear una array identidad de nx n.
- Paso 2: Realice operaciones de fila o columna en la array original (A) para que sea equivalente a la array identidad.
- Paso 3: Realice operaciones similares en la array de identidad también.
Ahora la array identidad resultante después de todas las operaciones es la array inversa .
Ejemplos
Nota:
Aquí, R1: Fila 1, R2: Fila 2, R3: Fila 3
Ejemplo 1: ¿Encontrar la inversa de la siguiente array mediante operaciones elementales?

Solución:
Realicemos operaciones de fila o columna en la array original (A) para que sea equivalente a la array identidad.
Paso 1: Intercambiar filas R2 y R3 (para hacer A[2][2] = 1)
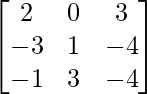
Paso 2: R1 = R1 + R3 (para hacer A[1][1] = 1)
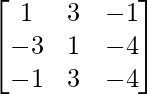
Paso 3: R2 = R2 – 3R3 (para hacer A[2][1] = 0)
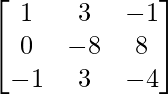
Paso 4: R3 = R3 + R1 (para hacer A[3][1] = 0)
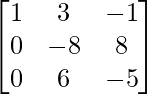
Paso 5: R2 = R2/-8 (para hacer A[2][2] = 1)
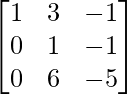
Paso 6: R1 = R1 – R2 (para hacer A[1][3] = 0)
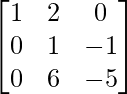
Paso 7: R3 – 6R2 (para hacer A[3][2] = 0)
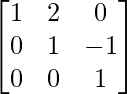
Paso 8: R2 = R2 + R3 (para hacer A[2][3] = 0)

Paso 9: R1 = R1 – 2R2 (para hacer A[1][2] = 0)
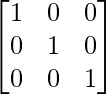
Ahora realice la misma operación anterior en la array de identidad. Resultado después de cada operación similar a la anterior en la array de identidad, obtenemos:
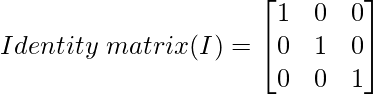
Paso 1: Intercambiar filas R2 y R3
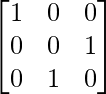
Paso 2: R1 = R1 + R3

Paso 3: R2 = R2 – 3R3
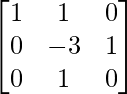
Paso 4: R3 = R3 + R1
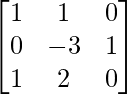
Paso 5: R2 = R2/-8
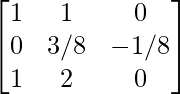
Paso 6: R1 = R1 – R2
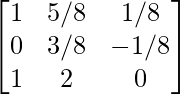
Paso 7: R3 – 6R2
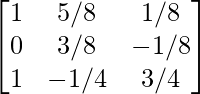
Paso 8: R2 = R2 + R3
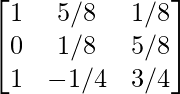
Paso 9: R1 = R1 – 2R2
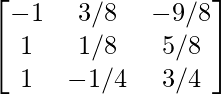
Entonces, la inversa de la array A es:
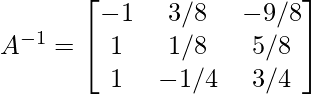
Ejemplo 2: ¿Encontrar la inversa de la siguiente array mediante operaciones elementales?
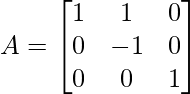
Solución:
Paso 1: R1 = R1 + R2
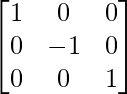
Paso 2: R2 = R2 x -1
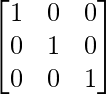
Operaciones similares en la array de identidad darán como resultado:
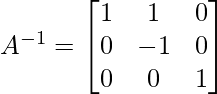
Ejemplo 3: ¿Encontrar la inversa de la siguiente array mediante operaciones elementales?
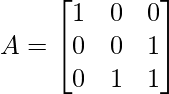
Solución:
Paso 1: Intercambiar R2 y R3
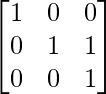
Paso 2: R2 = R2 – R3
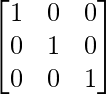
Operaciones similares en la array de identidad darán como resultado:
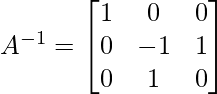
Publicación traducida automáticamente
Artículo escrito por aktmishra143 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA