Operaciones Matemáticas con Arrays | Clase 12 Matemáticas

Una array es un arreglo rectangular de números, símbolos o expresiones, organizados en filas y columnas. Una array puede tener ‘m’ número de filas y ‘n’ número de columnas, entonces se llama array m×n.

$\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}_{3\times 3}$

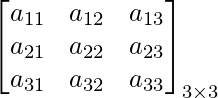
Las arrays se escriben entre corchetes donde las líneas horizontales se denominan filas, por ejemplo, en la array anterior: a ₁₁ , a ₁₂ , a ₁₃ .

Las líneas verticales se llaman columnas, por ejemplo, un ₁₁ , un ₂₁ , un ₃₁ . El tamaño de la array se decide por el número de filas y columnas.

Igualdad de Arrays

Se dice que dos arrays ‘A’ y ‘B’ son iguales si cumplen las siguientes tres condiciones;

Si el número de filas en la array ‘A’ y la array ‘B’ son iguales.
Si el número de columnas en la array ‘A’ y la array ‘B’ son iguales.
Los elementos correspondientes en la array ‘A’ y la array ‘B’ están en la misma posición.

$A= \begin{bmatrix} 2 & 9 & 3\\ 4 & 8 & 5\\ 1 & 5 & 7 \end{bmatrix}, B= \begin{bmatrix} 2 & 9 & 3\\ 4 & 8 & 5\\ 1 & 5 & 7 \end{bmatrix}$

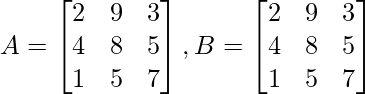
Aquí las arrays ‘A’ y ‘B’ son iguales ya que satisfacen las tres condiciones anteriores.

Problema: ¿Encuentra el valor de ‘x’ e ‘y’ si las siguientes arrays son iguales?

$A = \begin{bmatrix} x+5 & 3\\ 7& 8 \end{bmatrix}, B = \begin{bmatrix} 6 & 3\\ y-2 & 8 \end{bmatrix}$

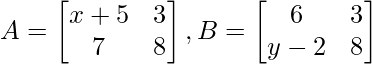
Solución:

Al igualar los elementos correspondientes podemos el valor de ‘x’ e ‘y’

x + 5 = 6
x = 6 – 5
x = 1

7 = y – 2
7 + 2 = y
y = 9

Adición de Arrays

En array, la suma de arrays es el funcionamiento de la suma de las dos arrays sumando los elementos correspondientes.
La condición para la suma de dos arrays es:
Las dos arrays deben ser del mismo orden o tamaño, es decir, el número de filas debe ser igual al número de columnas.

Ejemplo:

$A = \begin{bmatrix} 2 & 9\\ 5 & 6 \end{bmatrix}, B = \begin{bmatrix} 1 & 7\\ 2 & 3 \end{bmatrix}, C = \begin{bmatrix} 5 & 4 & 8\\ 2 & 3 & 7 \end{bmatrix}$

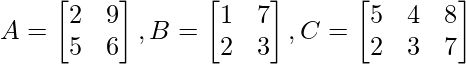
Aquí se pueden sumar las arrays ‘A’ y ‘B’ ya que ambas están en orden 2×2,

$A+B = \begin{bmatrix} 2+1 & 9+7\\ 5+2 & 6+3 \end{bmatrix}$
$A+B = \begin{bmatrix} 3 & 16\\ 7 & 9 \end{bmatrix}$

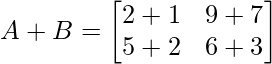
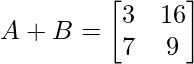
Además, ‘A’ + ‘C’ no se pueden sumar ya que no están en el mismo orden, la array ‘A’ es de orden 2×2 y la array ‘C’ es de orden 2×3.

Resta de Arrays

En array, la resta de arrays es el funcionamiento de la resta de las dos arrays al restar los elementos correspondientes entre sí.
La condición para la resta de dos arrays es:
Las dos arrays deben ser del mismo orden o tamaño, es decir, el número de filas debe ser igual al número de columnas.

Ejemplo:

$A = \begin{bmatrix} 9 & 3\\ 6 & 1 \end{bmatrix}, B = \begin{bmatrix} 5 &2\\ 8 & 7 \end{bmatrix}$

Aquí el orden en la array ‘A’ y ‘B’ 2×2,
restando los elementos correspondientes

$A-B =\begin{bmatrix} 9-5 & 3-2\\ 6-8 & 1-7 \end{bmatrix}$
$A-B =\begin{bmatrix} 4 & 1\\ -2 & -6\end{bmatrix}$

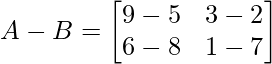
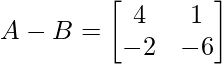
Multiplicar arrays por escalares

En la multiplicación escalar, cada elemento de una array se multiplica por un escalar. Aquí nos estamos refiriendo escalar a los números reales.

Propiedades de multiplicar arrays por escalares

Propiedad de dimensión

Si multiplicamos una array por un escalar la dimensión de la array no cambia queda igual como se explica en el siguiente ejemplo,

$2A = \begin{bmatrix} 7 & 5\\ 3 & 6 \end{bmatrix}_{2\times2} = \begin{bmatrix} 2\times7 & 2\times5\\ 2\times3 & 2\times6 \end{bmatrix}_{2\times2} = \begin{bmatrix} 14 & 10\\ 6 & 12 \end{bmatrix}_{2\times2}$

En el ejemplo anterior, cuando hemos multiplicado la array de dimensión 2×2 con el escalar 2, la array resultante también es de dimensión 2×2.

Propiedad conmutativa

Cambiar el orden de la array a multiplicar no cambia el resultado. Al multiplicar una array con el escalar, el orden en que se ordenan los factores en la multiplicación no hace ninguna diferencia en el resultado.
Por ejemplo: sea ‘a’ el escalar y ‘A’ la array
Por esta propiedad entendemos que

aa = aa

Ejemplo:

$3.A = 3\begin{bmatrix} 4 & 5\\ 2 & 1 \end{bmatrix} = \begin{bmatrix} 3\times4 & 3\times5\\ 3\times2 & 3\times1 \end{bmatrix} = \begin{bmatrix} 12 & 15\\ 6 & 3 \end{bmatrix}$
$A.3 = \begin{bmatrix} 4 & 5\\ 2 & 1 \end{bmatrix}3 = \begin{bmatrix} 4\times3 & 5\times3\\ 2\times3 & 1\times3 \end{bmatrix} = \begin{bmatrix} 12 & 15\\ 6 & 3 \end{bmatrix}$

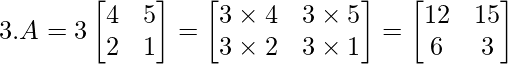
3.A = A.3

Propiedad asociativa

La multiplicación de una array es asociativa, es decir, al multiplicar una array por dos escalares, el orden de multiplicación de los escalares y la array no cambiará para dar como resultado. Sean ‘a’ y ‘b’ el escalar y ‘X’ la array, entonces,

(aX).b = a.(Xb)

Ejemplo: a = 2, b = 7. y X sea cualquier array de 2×2

$(a.X).b= (2.\begin{bmatrix} 1 & 4\\ 3 & 5 \end{bmatrix}).7 = \begin{bmatrix} 2\times1 & 2\times 4\\ 2\times 3 & 2\times 5 \end{bmatrix}.7 = \begin{bmatrix} 2 & 8\\ 6 & 10 \end{bmatrix}.7 = \begin{bmatrix} 2\times7 & 8\times7\\ 6\times 7 & 10\times7 \end{bmatrix} = \begin{bmatrix} 14 & 56\\ 42 & 70 \end{bmatrix}$

$a.(X.b)= 2.()\begin{bmatrix} 1 & 4\\ 3 & 5 \end{bmatrix}.7) = 2.\begin{bmatrix} 1\times7 & 4\times 7\\ 3\times 7 & 5\times 7 \end{bmatrix} = 2.\begin{bmatrix} 7 & 28\\ 21 & 35 \end{bmatrix} = \begin{bmatrix} 2\times7 & 2\times28\\ 2\times 21 & 2\times35 \end{bmatrix} = \begin{bmatrix} 14 & 56\\ 42 & 70 \end{bmatrix}$

(aX).b = a.(Xb)

Propiedad distributiva

La propiedad distributiva de las arrays establece que al multiplicar el escalar por las arrays ‘A’ y ‘B’ y la inclusión a la multiplicación también se aplican otras operaciones aritméticas como la suma o la resta. Usamos la propiedad distributiva para aclarar problemas en los que uno de los factores en la multiplicación de arrays escalares es una suma o una resta.

Ejemplo 1: Sea ‘a’ el escalar y ‘A’ y ‘B’ las arrays.
a.(A + B) = aA + aB

$a.(A+B) =2.(\begin{bmatrix} 1 & 2\\ 4 & 3 \end{bmatrix} + \begin{bmatrix} 2 & 4\\ 3 & 5 \end{bmatrix}) = 2.\begin{bmatrix} 3 & 6\\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 12\\ 14 & 16 \end{bmatrix}$
$a.A+ a.B =(2.\begin{bmatrix} 1 & 2\\ 4 & 3 \end{bmatrix}) + (2.\begin{bmatrix} 2 & 4\\ 3 & 5 \end{bmatrix}) = \begin{bmatrix} 2 & 4\\ 8 & 6 \end{bmatrix} + \begin{bmatrix} 4 & 8\\ 6 & 10 \end{bmatrix} = \begin{bmatrix} 6 & 12\\ 14 & 16 \end{bmatrix}$

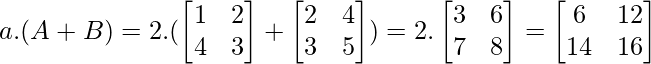
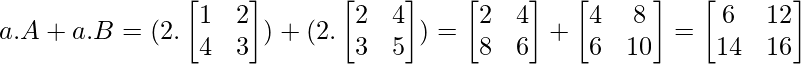
a.(A+B) = aA + aB

Ejemplo 2: Si una de las operaciones en la multiplicación es la suma de escalares, entonces la propiedad distributiva viene dada por
Sean ‘a’ y ‘b’ escalares y ‘A’ la array.
(a+b).A = aA +bA

$(a+b).A = (1+2).\begin{bmatrix} 5 &4 \\ 2 &1 \end{bmatrix} = 3.\begin{bmatrix} 5 & 4\\ 2 & 1 \end{bmatrix} = \begin{bmatrix} 15 &12 \\ 6 & 3 \end{bmatrix}$
$a.A+b.A = 1.\begin{bmatrix} 5 &4 \\ 2 &1 \end{bmatrix} + 2.\begin{bmatrix} 5 &4 \\ 2 &1 \end{bmatrix} = \begin{bmatrix} 5 & 4\\ 2 & 1 \end{bmatrix} + \begin{bmatrix} 10 & 8\\ 4 & 2 \end{bmatrix} = \begin{bmatrix} 15 &12 \\ 6 & 3 \end{bmatrix}$

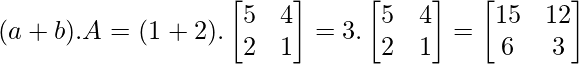
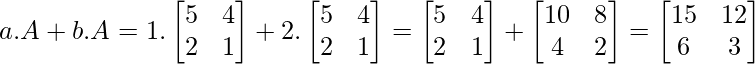
Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Igualdad de Arrays

Adición de Arrays

Resta de Arrays

Multiplicar arrays por escalares

Propiedades de multiplicar arrays por escalares

Deja una respuesta Cancelar la respuesta