propiedades de la suma de arrays y la multiplicación escalar | Clase 12 Matemáticas

Una array es simplemente una array rectangular o un conjunto de elementos. La Array se puede definir como un elemento m*n en forma de m líneas horizontales (filas), n líneas verticales (columnas) conocidas como array de orden m*n. Los elementos pueden ser números reales, complejos o desconocidos. Una array m*n claramente se parece a:

En la figura anterior se dibuja una array de orden m*n donde I y j representan la posición exacta del elemento (i,j).

Tipos de Arrays

Hay muchos tipos de arrays disponibles, algunas de ellas se mencionan a continuación.

Array de filas

Una array que tiene una sola fila se llama array fila. 

Ejemplo: 

Array de columnas

Una array que tiene una sola columna se conoce como array columna. 

Ejemplo: 

Array cero o nula

Una array que tiene todos los elementos como 0 se conoce como array cero o nula. 

Ejemplo : 

Array cuadrada

Una array que tiene el mismo número de columnas y filas se conoce como array cuadrada. 

Ejemplo : 

Array diagonal

Una array en la que todos los elementos son cero excepto los elementos diagonales se conoce como array diagonal. 

Ejemplo : 

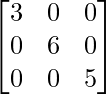
array escalar

Un tipo especial de array diagonal en la que todos los elementos diagonales son iguales se conoce como array escalar. 

Ejemplo :

Array de identidad

La array identidad es una array escalar en la que todos los elementos diagonales son 1. 

Ejemplo : 

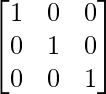
Propiedades de la array cero

Cuando sumamos o restamos la array 0 de orden m*n de cualquier otra array, devuelve la misma Array. En palabras simples, “A+0 = A” y “A – 0 = A”.

Ejemplo : 

De manera similar, puede ver que la resta de una array nula de cualquier otra array dará como resultado la otra array.

Entre todos los tipos de arrays, solo el rango de array cero es siempre cero en todos los casos de multiplicación.

Propiedades de la Adición de Arrays

Una array se puede sumar con otra array si y solo si el orden de las arrays es el mismo. La suma se realizará entre los elementos de las arrays. La array resultante también será del mismo orden. Eso es [A]m×n + [B]m×n = [C]m×n 

Por ejemplo:

Hay varias propiedades únicas de la adición de arrays. Discutiremos las propiedades mencionadas a continuación:

1. Propiedad conmutativa de la suma, es decir, A + B = B+ A
2. Propiedad asociativa de la suma, es decir, A+ (B + C) = (A + B) + C
3. Propiedad de identidad aditiva. Para cualquier array A, existe una única array O tal que, A+O = A
4. Propiedad inversa aditiva. Cuando sumamos una array única –A a A, obtenemos la array O, A+ (-A) = O.
5. Cierre Propiedad de la suma A + B = C, donde C es una array de las mismas dimensiones que A y B.

A, B y C son arrays del mismo orden m*n. Para sumar dos Arrays que tengan el mismo orden, basta con sumar el elemento correspondiente de cada Array. Discutamos la propiedad de suma de Matrix en detalle.

Propiedad conmutativa de la suma de arrays

Esta propiedad informa que dos arrays cualesquiera del mismo orden se pueden sumar de cualquier forma. Supongamos que hay dos arrays A y B del mismo orden m*n, entonces la propiedad conmutativa de la suma de arrays establece que: A + B = B + A

Ejemplo : 

En el ejemplo anterior, puede ver que la suma de Matrix sigue la ley conmutativa.

Propiedad asociativa de la suma de arrays

De manera similar, si tres arrays tienen el mismo orden, su posición tampoco importa. Supongamos que hay tres arrays A, B y C de orden m*n, entonces la propiedad asociativa de la suma de arrays establece que: A + (B + C) = (A + B) + C

Ejemplo:

En el ejemplo anterior, puede ver que la suma de arrays sigue la ley asociativa.

Propiedad de identidad aditiva de la suma de arrays

Hemos discutido Array cero que la array O se puede agregar a cualquier array para obtener el mismo resultado. Según la propiedad de identidad aditiva de la suma de arrays, para una array A dada de orden m*n, existe una array O de m*n tal que: A + O = A

Aquí, O es la array m*n de orden cero.

Entonces, si agrega una array a una array cero, obtiene la array original.

Propiedad inversa aditiva de la suma de arrays

Hay una regla en Matrix que la inversa de cualquier array A es –A del mismo orden. En palabras simples, para una array A dada de orden m*n, existe una única array B tal que: A + B = O

Nota: Esta array B es igual a –A, es decir, B = -A

Por lo tanto, A + (-A) = O

Ejemplo:

Hemos discutido las diversas propiedades de la suma de arrays. Ahora discutiremos algunas propiedades únicas de la multiplicación escalar de arrays.

Propiedades de la multiplicación escalar de arrays

El término multiplicación escalar se refiere al producto de una array y un número real. Cada entrada se multiplica por un escalar dado en la multiplicación escalar. Un escalar es un número real en la multiplicación escalar.

Ejemplo:

Por lo tanto, está claro que Matrix se puede multiplicar por cualquier cantidad escalar. 

La multiplicación de arrays tiene algunas propiedades únicas; algunos de ellos se enumeran a continuación:

1. Propiedad asociativa de la multiplicación, es decir, (cd)A = c(dA)
2. Propiedad distributiva, es decir, c[A + B] = c[A] + c[B]
3. Propiedad de identidad multiplicativa, es decir, 1.A = A
4. Propiedad multiplicativa de cero, es decir, 0.A = 0 c.0 = 0
5. Propiedad de cierre de la multiplicación cA es una array de la misma dimensión que A

Nota: A es una array de orden m*n, c y d son escalares y O es una array cero.

Propiedad asociativa de la multiplicación escalar de arrays:

De acuerdo con la propiedad asociativa de la multiplicación, si una array se multiplica por dos escalares, los escalares se pueden multiplicar juntos primero, luego el resultado se puede multiplicar por la Array o la Array se puede multiplicar por un escalar primero y luego la Array resultante por el otro escalar, es decir (cd)A = c(dA)

Por ejemplo: 

Aquí estamos tomando dos escalares como 2 y 3.

Asi que, 

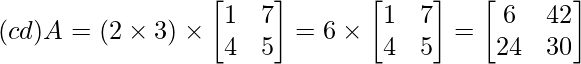
En el ejemplo anterior, puede ver que el resultado es el mismo en ambos casos.

Propiedad distributiva de la multiplicación escalar de arrays

La propiedad distributiva prueba claramente que una cantidad escalar puede distribuirse sobre una suma matricial o una Array distribuida sobre una suma escalar.

1. c(A + B) = cA + cB

Por ejemplo:

2. (c + d)A = cA + dA

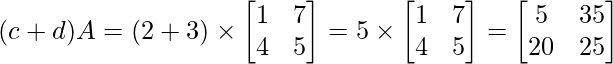
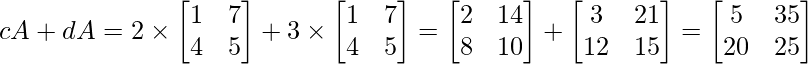
Propiedad de identidad multiplicativa de la multiplicación escalar de arrays

Si cualquier array A se multiplica por el escalar 1, el resultado es simplemente la array original A.

1.A = A

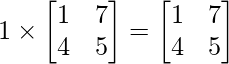
Nota: El escalar 1 será identidad multiplicativa en la multiplicación escalar.

Propiedad multiplicativa del cero

De acuerdo con la propiedad multiplicativa del cero, si cualquier array A de orden m*n se multiplica por el escalar 0, entonces el resultado es la array O de m*n cero. Esto sigue las propiedades multiplicativas del cero en el sistema de números reales. Si cualquier número real x se multiplica por 0, el resultado siempre es 0. Si cualquier escalar se multiplica por la array cero, el resultado es el mismo que la array cero.  

0.A = 0

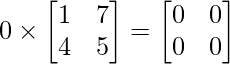
c.0 = 0

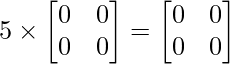
Propiedad de cierre de la multiplicación escalar de arrays

La propiedad de cierre simplemente establece que si tiene una cantidad escalar X y una array A del mismo orden m*n, entonces cada elemento se multiplicará por X. Esta propiedad establece que si cualquier array A de orden m*n se multiplica por cualquier escalar, entonces el orden de Matrix sigue siendo el mismo que m*n.