Tipos de gráficos y aplicaciones

Prerrequisito: Fundamentos de la teoría de grafos – Conjunto 1 , Fundamentos de la teoría de grafos – Conjunto 2 

Un grafo G = (V, E) consta de un conjunto de vértices V = { V1, V2, . . . } y conjunto de aristas E = { E1, E2, . . . }. El conjunto de pares desordenados de vértices distintos cuyos elementos se denominan aristas del grafo G tal que cada arista se identifica con un par desordenado (Vi, Vj) de vértices. Se dice que los vértices (Vi, Vj) son adyacentes si existe una arista Ek que está asociada a Vi y Vj. En tal caso, Vi y Vj se denominan puntos extremos y se dice que la arista Ek es la conexión/unión de Vi y Vj. 

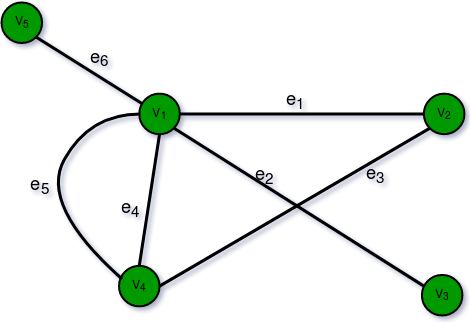Tipos de gráfico:

• Gráficos finitos: se dice que un gráfico es finito si tiene un número finito de vértices y un número finito de aristas. 

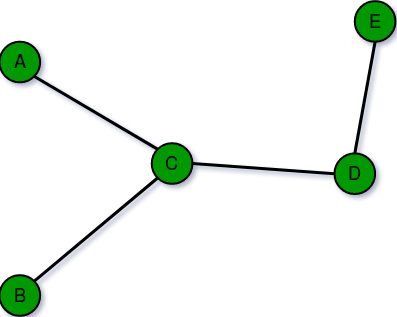
• Gráfico infinito: se dice que un gráfico es infinito si tiene un número infinito de vértices y un número infinito de aristas.
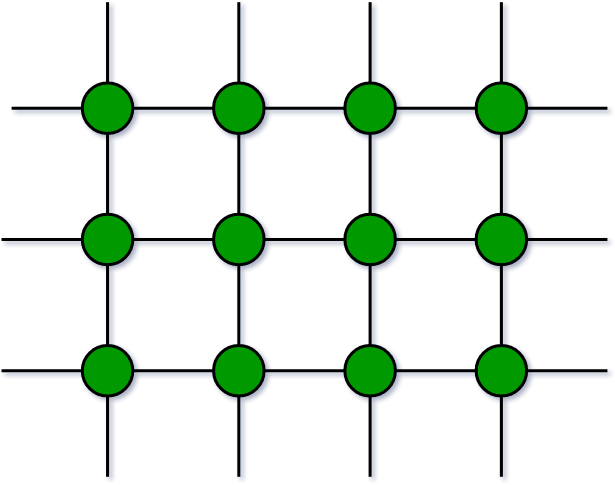
• Gráfico trivial: se dice que un gráfico es trivial si un gráfico finito contiene solo un vértice y ningún borde.
• Gráfico simple: un gráfico simple es un gráfico que no contiene más de un borde entre el par de vértices. Una vía férrea simple que conecta diferentes ciudades es un ejemplo de gráfico simple.
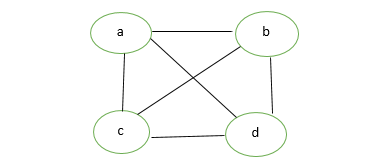
• Gráfico múltiple: cualquier gráfico que contenga algunos bordes paralelos pero que no contenga ningún bucle automático se denomina gráfico múltiple. Por ejemplo, una hoja de ruta.
  • Bordes paralelos: si dos vértices están conectados con más de un borde, dichos bordes se denominan bordes paralelos, es decir, muchas rutas pero un destino.
  • Bucle: un borde de un gráfico que comienza en un vértice y termina en el mismo vértice se denomina bucle o autobucle.
• Gráfico nulo: un gráfico de orden n y tamaño cero es un gráfico donde solo hay vértices aislados sin bordes que conectan cualquier par de vértices.

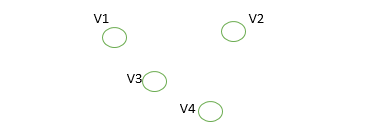
• Orden de un grafo : Número de vértices en un grafo.
• Tamaño de un gráfico : número de aristas en un gráfico.
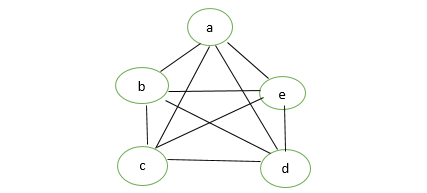
• Gráfico completo: un gráfico simple con n vértices se llama gráfico completo si el grado de cada vértice es n-1, es decir, un vértice está unido con n-1 aristas o el resto de los vértices en el gráfico. Un gráfico completo también se llama Gráfico completo.
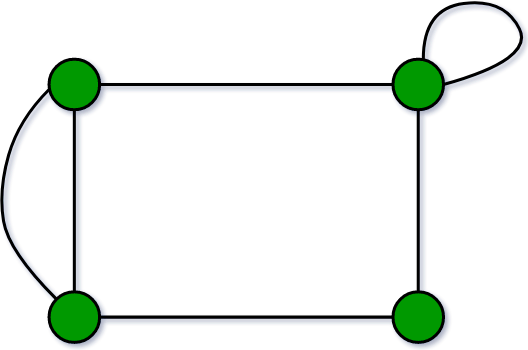
• Pseudografo: Un grafo G con un bucle propio y algunos bordes múltiples se llama pseudografo.
• Gráfico regular: Se dice que un gráfico simple es regular si todos los vértices de un gráfico G son del mismo grado. Todos los gráficos completos son regulares pero viceversa no es posible.
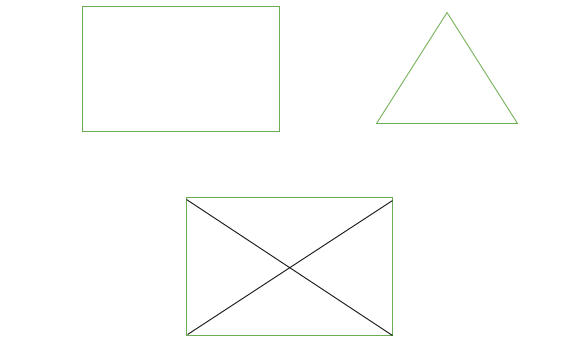
• Gráfico bipartito: se dice que un gráfico G = (V, E) es un gráfico bipartito si su conjunto de vértices V (G) se puede dividir en dos subconjuntos disjuntos no vacíos. V1(G) y V2(G) de tal forma que cada arista e de E(G) tiene su un extremo en V1(G) y el otro en V2(G). La partición V1 U V2 = V se llama Bipartita de G. Aquí en la figura: V1(G)={V5, V4, V3} y V2(G)={V1, V2}
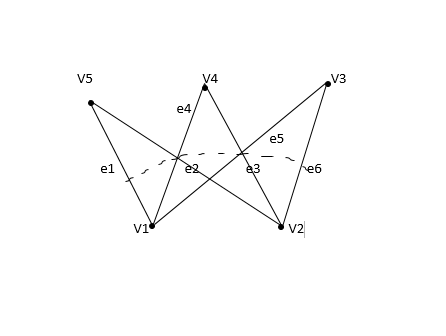
• Gráfico etiquetado: si los vértices y los bordes de un gráfico están etiquetados con nombre, datos o peso, entonces se llama gráfico etiquetado. También se le llama gráfico ponderado . 

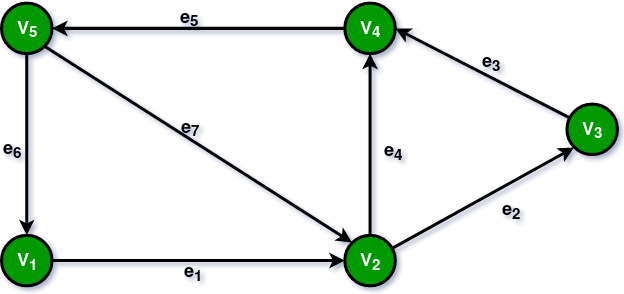
• Digraph Graph: Un gráfico G = (V, E) con un mapeo f tal que cada borde se mapea en algún par ordenado de vértices (Vi, Vj) se llama Digraph. También se le llama gráfico dirigido . Par ordenado (Vi, Vj) significa un borde entre Vi y Vj con una flecha dirigida de Vi a Vj. Aquí en la figura: e1 = (V1, V2) e2 = (V2, V3) e4 = (V2, V4)
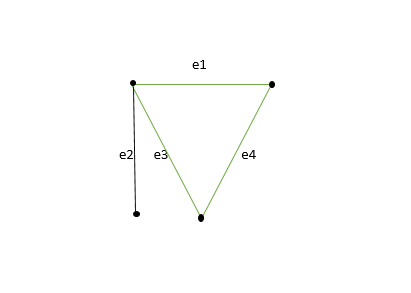
• Subgrafo: Un grafo G1 = (V1, E1) se llama subgrafo de un grafo G(V, E) si V1(G) es un subconjunto de V(G) y E1(G) es un subconjunto de E(G) tal que cada borde de G1 tiene los mismos vértices finales que en G. 

 

• Tipos de subgrafo:
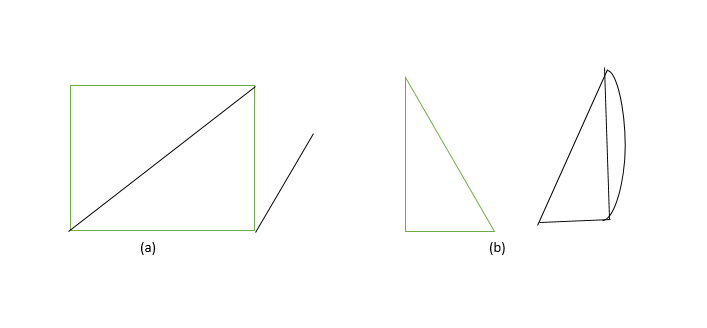
  • Subgrafo disjunto de vértice: se dice que dos gráficos G1 = (V1, E1) y G2 = (V2, E2) son disjuntos de vértice de un gráfico G = (V, E) si V1 (G1) intersección V2 (G2) = nulo . En la figura no hay un vértice común entre G1 y G2.
  • Subgrafo disjunto de aristas: Se dice que un subgrafo es disjunto de aristas si E1(G1) intersección E2(G2) = nulo. En la figura no hay arista común entre G1 y G2.

Nota: El subgrafo disjunto de borde puede tener vértices en común, pero el gráfico disjunto de vértice no puede tener un borde común, por lo que el subgrafo disjunto de vértice siempre será un subgrafo disjunto de borde.

• Grafo conexo o desconectado: Se dice que un grafo G es conexo si cualquier par de vértices (Vi, Vj) de un grafo G son alcanzables entre sí. O se dice que un grafo es conexo si existe al menos un camino entre todos y cada uno de los pares de vértices del grafo G, en caso contrario es inconexo. Un gráfico nulo con n vértices es un gráfico desconectado que consta de n componentes. Cada componente consta de un vértice y ningún borde.
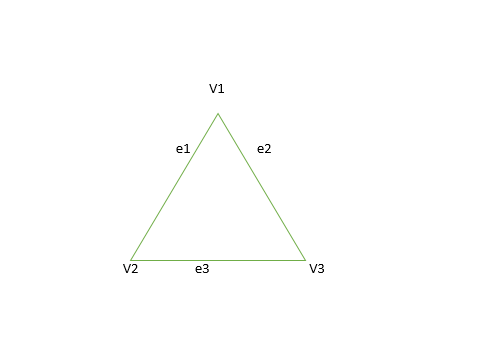
• Gráfico cíclico: Un gráfico G que consta de n vértices y n> = 3 que es V1, V2, V3- – – – – – – – Vn y aristas (V1, V2), (V2, V3), (V3, V4) – – – – – – – – — -(Vn, V1) se denominan gráficos cíclicos.

 Ventaja:

1. Son útiles para implementar algoritmos como DFS y BFS.
2. El gráfico proporciona precisión de datos.
3. Los gráficos son útiles para encontrar el camino más corto.
4. Para encontrar el árbol de expansión mínimo.
5. Se utiliza en problemas complejos.
6. Es útil para organizar datos.

Desventajas:

1. Los gráficos hacen que las estructuras de datos sean complejas ya que usan punteros.
2. Un gráfico puede tener una gran complejidad de memoria.
3. El gráfico está representado por una array de adyacencia que no permite bordes paralelos.
4. La multiplicación en un gráfico es compleja.
    

Aplicación de gráficos:

• Informática: en informática, el gráfico se utiliza para representar redes de comunicación, organización de datos, dispositivos informáticos, etc.
• Física y química: la teoría de grafos también se usa para estudiar moléculas en química y física.
• Ciencias sociales: la teoría de grafos también se usa ampliamente en sociología.
• Matemáticas: en esto, los gráficos son útiles en geometría y ciertas partes de la topología, como la teoría de nudos.
• Biología: la teoría de grafos es útil en biología y esfuerzos de conservación.
• El mapa de Google también usa gráficos. Es útil averiguar cuál es un lugar excelente tanto desde la ubicación como desde su ubicación cercana. En GPS también usamos gráficos.
• Facebook usa gráficos. El uso de gráficos sugiere amigos en común. muestra una lista de las siguientes páginas, amigos y lista de contactos.
• Microsoft Excel usamos Gráficos Acíclicos Dirigidos .
• En el algoritmo de Dijkstra, usamos un gráfico.
• En los sitios de redes sociales, usamos gráficos para rastrear los datos de los usuarios. Me gustó mostrar sugerencias .
•  En informática como el Algoritmo de Dijkstra, el Algoritmo de Prims, el Algoritmo de Kruskal

Aplicación de la vida real:

1. Mercadeo en Redes Sociales
2. Algoritmos para motores de búsqueda
3. Resolviendo Sudokus
4. Direcciones en un mapa
5. Programación de Aerolíneas.