Dados dos lados A, B y el ángulo C. Encuentra el tercer lado del triángulo usando la ley de los cosenos.
Ejemplos:
Input : a = 5, b = 8, c = 49 Output : 6.04339
En particular, la Ley de los cosenos se puede usar para encontrar la longitud del tercer lado de un triángulo cuando conoces la longitud de dos lados y el ángulo entre ellos. Vea aquí para aprender a encontrar el valor de cos.
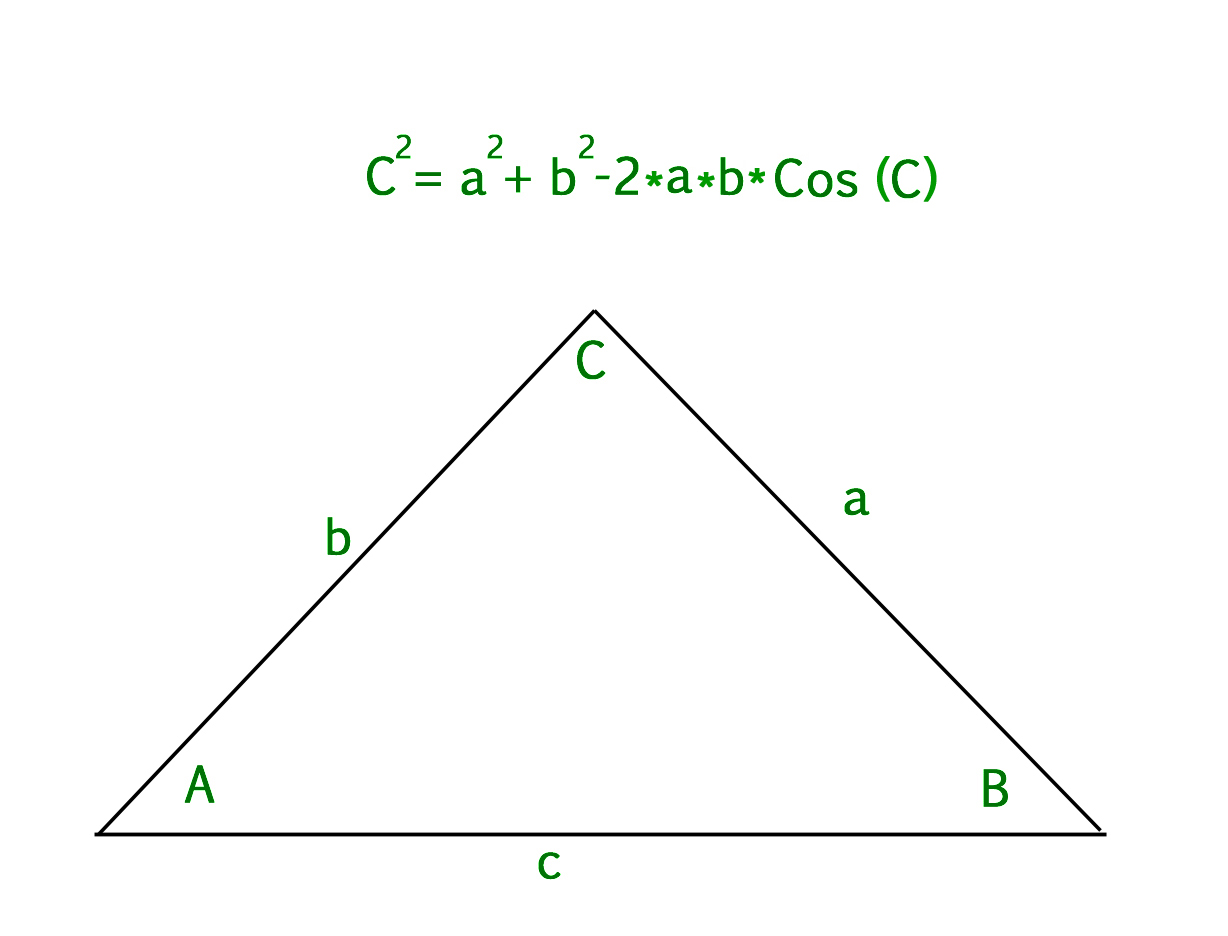
Supongamos que a, b, c son los lados del triángulo donde c es el lado opuesto al ángulo C. Entonces,
c^2 = a^2 + b^2 - 2*a*b*cos(c) OR c = sqrt(a^2 + b^2 - 2*a*b*cos(c))
C++
// CPP program to find third
// side of triangle using
// law of cosines
#include <bits/stdc++.h>
using namespace std;
// Function to calculate cos value of angle c
float cal_cos(float n)
{
float accuracy = 0.0001, x1, denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
x1 = 1;
// Maps the sum along the series
cosx = x1;
// Holds the actual value of sin(n)
cosval = cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= fabs(cosval - cosx));
return cosx;
}
// Function to find third side
float third_side(int a, int b, float c)
{
float angle = cal_cos(c);
return sqrt((a * a) + (b * b) - 2 * a * b * angle);
}
// Driver program to check the above function
int main()
{
float c = 49;
int a = 5, b = 8;
// function call
cout << third_side(a, b, c);
return 0;
}
Java
// Java program to find third
// side of triangle using
// law of cosines
class GFG
{
// Function to calculate
// cos value of angle c
static float cal_cos(float n)
{
float accuracy = 0.0001f, x1;
float denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142f / 180.0f);
x1 = 1;
// Maps the sum along the series
cosx = x1;
// Holds the actual value of sin(n)
cosval = (float)Math.cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <=
Math.abs(cosval - cosx));
return cosx;
}
// Function to find third side
static float third_side(int a,
int b, float c)
{
float angle = cal_cos(c);
return (float)Math.sqrt((a * a) +
(b * b) - 2 * a * b * angle);
}
// Driver code
public static void main (String[] args)
{
float c = 49;
int a = 5, b = 8;
// function call
System.out.print(Math.round(third_side(a,
b, c)*100000.0)/100000.0);
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 program to find third side # of triangle using law of cosines import math as mt # Function to calculate cos # value of angle c def cal_cos(n): accuracy = 0.0001 x1, denominator, cosx, cosval = 0, 0, 0, 0 # Converting degrees to radian n = n * (3.142 / 180.0) x1 = 1 # Maps the sum along the series cosx = x1 # Holds the actual value of sin(n) cosval = mt.cos(n) i = 1 while (accuracy <= abs(cosval - cosx)): denominator = 2 * i * (2 * i - 1) x1 = -x1 * n * n / denominator cosx = cosx + x1 i = i + 1 return cosx # Function to find third side def third_side(a, b, c): angle = cal_cos(c) return mt.sqrt((a * a) + (b * b) - 2 * a * b * angle) # Driver Code c = 49 a, b = 5, 8 print(third_side(a, b, c)) # This code is contributed by mohit kumar
C#
// C# program to find third
// side of triangle using
// law of cosines
using System;
class GFG
{
// Function to calculate
// cos value of angle c
static float cal_cos(float n)
{
float accuracy = 0.0001f, x1;
float denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142f / 180.0f);
x1 = 1;
// Maps the sum along the series
cosx = x1;
// Holds the actual value of sin(n)
cosval = (float)Math.Cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <=
Math.Abs(cosval - cosx));
return cosx;
}
// Function to find third side
static float third_side(int a,
int b, float c)
{
float angle = cal_cos(c);
return (float)Math.Sqrt((a * a) +
(b * b) - 2 * a * b * angle);
}
// Driver code
public static void Main ()
{
float c = 49;
int a = 5, b = 8;
// function call
Console.WriteLine(Math.Round(third_side(a,
b, c)*100000.0)/100000.0);
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find third
// side of triangle using
// law of cosines
// Function to calculate
// cos value of angle c
function cal_cos( $n )
{
$accuracy = 0.0001;
$x1; $denominator;
$cosx; $cosval;
// Converting degrees
// to radian
$n = $n * (3.142 / 180.0);
$x1 = 1;
// Maps the sum
// along the series
$cosx = $x1;
// Holds the actual
// value of sin(n)
$cosval = cos($n);
$i = 1;
do
{
$denominator = 2 * $i *
(2 * $i - 1);
$x1 = -$x1 * $n * $n /
$denominator;
$cosx = $cosx + $x1;
$i = $i + 1;
} while ($accuracy <= ($cosval -
$cosx));
return $cosx;
}
// Function to find third side
function third_side($a, $b, $c)
{
$angle = cal_cos($c);
return sqrt(($a * $a) +
($b * $b) - 2 *
$a * $b * $angle);
}
// Driver Code
$c = 49;
$a = 5;
$b = 8;
// function call
echo third_side($a, $b, $c);
// This code is contributed
// by ajit
?>
Javascript
<script>
// Javascript program to find third
// side of triangle using
// law of cosines
// Function to calculate
// cos value of angle c
function cal_cos( n) {
let accuracy = 0.0001, x1;
let denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
x1 = 1;
// Maps the sum alet the series
cosx = x1;
// Holds the actual value of sin(n)
cosval = Math.cos(n);
let i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= Math.abs(cosval - cosx));
return cosx;
}
// Function to find third side
function third_side( a, b, c) {
let angle = cal_cos(c);
return Math.sqrt((a * a) + (b * b) - 2 * a * b * angle);
}
// Driver code
let c = 49;
let a = 5, b = 8;
// function call
document.write(Math.round(third_side(a, b, c) * 100000.0) / 100000.0);
// This code is contributed by Rajput-Ji
</script>
Producción
6.04339
Complejidad de tiempo : O (log (n)), ya que usa la función sqrt incorporada
Espacio auxiliar : O (1), ya que no estamos usando ningún espacio adicional.