El Teorema de Vantieghem es una condición necesaria y suficiente para que un número sea primo. Establece que para que un número natural n sea primo, el producto de ![]() donde
donde ![]() , es congruente con
, es congruente con ![]() .
.
En otras palabras, un número n es primo si y solo si. 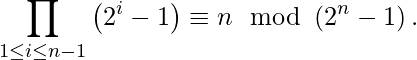
Ejemplos:
- Para n = 3, el producto final es (2 1 – 1) * (2 2 – 1) = 1*3 = 3. 3 es congruente con 3 mod 7. Obtenemos 3 mod 7 de la expresión 3 * (mod (2 3 – 1)), por lo tanto 3 es primo.
- Para n = 5, el producto final es 1*3*7*15 = 315. 315 es congruente con 5 (mod 31), por lo tanto, 5 es primo.
- Para n = 7, el producto final es 1*3*7*15*31*63 = 615195. 615195 es congruente con 7 (mod 127), por lo tanto, 7 es primo.
- Para n = 4, el producto final 1*3*7 = 21. 21 no es congruente con 4 (mod 15), por lo tanto, 4 es compuesto.
Otra forma de establecer el teorema anterior es, si ![]() divide
divide ![]() a n, entonces n es primo.
a n, entonces n es primo.
C++
// C++ code to verify Vantieghem's Theorem
#include <bits/stdc++.h>
using namespace std;
void checkVantieghemsTheorem(int limit)
{
long long unsigned prod = 1;
for (long long unsigned n = 2; n < limit; n++) {
// Check if above condition is satisfied
if (((prod - n) % ((1LL << n) - 1)) == 0)
cout << n << " is prime\n";
// product of previous powers of 2
prod *= ((1LL << n) - 1);
}
}
// Driver code
int main()
{
checkVantieghemsTheorem(10);
return 0;
}
Java
// Java code to verify Vantieghem's Theorem
import java.util.*;
class GFG
{
static void checkVantieghemsTheorem(int limit)
{
long prod = 1;
for (long n = 2; n < limit; n++)
{
// Check if above condition is satisfied
if (((prod - n < 0 ? 0 : prod - n) % ((1 << n) - 1)) == 0)
System.out.print(n + " is prime\n");
// product of previous powers of 2
prod *= ((1 << n) - 1);
}
}
// Driver code
public static void main(String []args)
{
checkVantieghemsTheorem(10);
}
}
// This code is contributed by rutvik_56.
Python3
# Python3 code to verify Vantieghem's Theorem def checkVantieghemsTheorem(limit): prod = 1 for n in range(2, limit): # Check if above condition is satisfied if n == 2: print(2, "is prime") if (((prod - n) % ((1 << n) - 1)) == 0): print(n, "is prime") # Product of previous powers of 2 prod *= ((1 << n) - 1) # Driver code checkVantieghemsTheorem(10) # This code is contributed by shubhamsingh10
C#
// C# code to verify Vantieghem's Theorem
using System;
class GFG
{
static void checkVantieghemsTheorem(int limit)
{
long prod = 1;
for (long n = 2; n < limit; n++)
{
// Check if above condition is satisfied
if (((prod - n < 0 ? 0 : prod - n) % ((1 << (int)n) - 1)) == 0)
Console.Write(n + " is prime\n");
// product of previous powers of 2
prod *= ((1 << (int)n) - 1);
}
}
// Driver code
public static void Main()
{
checkVantieghemsTheorem(10);
}
}
// This code is contributed by pratham76.
Javascript
<script>
// Javascript code to verify Vantieghem's Theorem
function checkVantieghemsTheorem( limit)
{
let prod = 1;
for (let n = 2; n < limit; n++) {
// Check if above condition is satisfied
if (n == 2)
document.write(2 + " is prime" + "</br>");
if (((prod - n) % ((1 << n) - 1)) == 0)
document.write( n + " is prime" + "</br>");
// product of previous powers of 2
prod *= ((1 << n) - 1);
}
}
// Driver Code
checkVantieghemsTheorem(10);
// This code is contributed by jana_sayantan.
</script>
Producción:
2 is prime 3 is prime 5 is prime 7 is prime
El código anterior no funciona para valores de n superiores a 11. Provoca desbordamiento en la evaluación de producción.
Publicación traducida automáticamente
Artículo escrito por jaideeppyne1997 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA