Dibujo de línea suavizada A
continuación se muestra la imagen que muestra la línea dibujada con el algoritmo de línea de Bresenham (izquierda) y el algoritmo de línea de Xiaolin Wu (derecha) que suaviza la línea. ¿Cuál te parece mejor? Concepto de Anti Aliasing Supongamos que queremos dibujar una línea desde el punto (1, 1) al punto (8, 4) con bordes rectangulares. La línea ideal sería la que se muestra en la figura A. Como quiero mostrarlo en la pantalla, no puedo usar eso. La línea debe pasar por un proceso llamado Rasterización que determinaría el color de los píxeles individuales. Se pueden usar varios algoritmos como el algoritmo de línea de Bresenham , el analizador diferencial digital , el algoritmo de línea de Xiaolin Wu, el algoritmo de Gupta-Sproull. Más tarde, dos realizan anti-aliasing o suavizado de líneas.
El resultado producido por los dos primeros algoritmos se muestra en la figura B.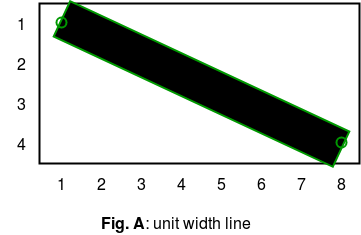
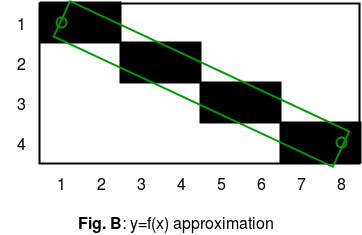
Hay pocos problemas en Línea (figura B).
1. Pixel (4,2) tiene menos cobertura que Pixel (3,2), pero ambos están dibujados completamente en negro.
2. El píxel (2,2) tiene casi tanta cobertura como (4,2) y, sin embargo, se dibuja completamente en blanco.
Para superar estos inconvenientes y producir una línea mucho más suave, usamos el algoritmo de línea de Xiaolin Wu.
Algoritmo de línea de Xiaolin Wu
Considere la figura que se muestra a continuación, que se dibuja utilizando el Algoritmo de generación de línea de Bresenham. Tome un segmento y su coordenada inicial x. Por la X en el bucle se suma 1 hacia el final del segmento. En cada paso, se calcula el error: la distancia entre la coordenada y real en esa ubicación y la celda de cuadrícula más cercana. Si el error no supera la mitad de la altura de la celda, se rellena. Ese es todo el algoritmo. Modificaremos este algoritmo para que pueda producir una línea suavizada.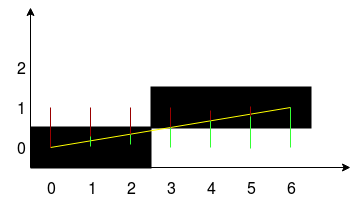
El algoritmo de línea de Xiaolin Wu se caracteriza por el hecho de que en cada paso del cálculo se realiza para los dos más cercanos a la línea de píxeles, y se colorean con diferente intensidad, dependiendo de la distancia. La intensidad del píxel central de la intersección actual da el 100% si el píxel está dentro de los 0,9 píxeles, la intensidad será del 10%. En otras palabras, el cien por cien de la intensidad se divide entre los píxeles que limitan la línea del vector en ambos lados. En la imagen, el color rojo y verde muestra la distancia a los dos píxeles adyacentes. Para calcular el error, puede usar el punto flotante y tomar el valor del error de la parte fraccionaria.
NOTA: La siguiente implementación usa la biblioteca SDL para dibujar píxeles en la pantalla. Si está en un sistema Debian como ubuntu, simplemente ejecute el siguiente comando para instalar la biblioteca SDL.
sudo apt-get install libsdl2-dev
Para construir uso
gcc filename.c -lSDL2
Nota: si la proyección del segmento en el eje x es menor que la proyección en el eje y, o si se intercambian el principio y el final del segmento, el algoritmo no funcionará. Para evitar esto, debe verificar la dirección del vector y su pendiente, y luego intercambiar las coordenadas de la línea, en última instancia, para reducir todo a uno o al menos dos casos.
El siguiente algoritmo asume que solo se proporcionarán coordenadas enteras como entradas, ya que el valor del píxel no puede ser un punto flotante.
// C program to implement Xiaolin Wu's line drawing
// algorithm.
// We must install SDL library using above steps
// to run this program
#include<SDL2/SDL.h>
// SDL stuff
SDL_Window* pWindow = 0;
SDL_Renderer* pRenderer = 0;
// swaps two numbers
void swap(int* a , int*b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// returns absolute value of number
float absolute(float x )
{
if (x < 0) return -x;
else return x;
}
//returns integer part of a floating point number
int iPartOfNumber(float x)
{
return (int)x;
}
//rounds off a number
int roundNumber(float x)
{
return iPartOfNumber(x + 0.5) ;
}
//returns fractional part of a number
float fPartOfNumber(float x)
{
if (x>0) return x - iPartOfNumber(x);
else return x - (iPartOfNumber(x)+1);
}
//returns 1 - fractional part of number
float rfPartOfNumber(float x)
{
return 1 - fPartOfNumber(x);
}
// draws a pixel on screen of given brightness
// 0<=brightness<=1. We can use your own library
// to draw on screen
void drawPixel( int x , int y , float brightness)
{
int c = 255*brightness;
SDL_SetRenderDrawColor(pRenderer, c, c, c, 255);
SDL_RenderDrawPoint(pRenderer, x, y);
}
void drawAALine(int x0 , int y0 , int x1 , int y1)
{
int steep = absolute(y1 - y0) > absolute(x1 - x0) ;
// swap the co-ordinates if slope > 1 or we
// draw backwards
if (steep)
{
swap(&x0 , &y0);
swap(&x1 , &y1);
}
if (x0 > x1)
{
swap(&x0 ,&x1);
swap(&y0 ,&y1);
}
//compute the slope
float dx = x1-x0;
float dy = y1-y0;
float gradient = dy/dx;
if (dx == 0.0)
gradient = 1;
int xpxl1 = x0;
int xpxl2 = x1;
float intersectY = y0;
// main loop
if (steep)
{
int x;
for (x = xpxl1 ; x <=xpxl2 ; x++)
{
// pixel coverage is determined by fractional
// part of y co-ordinate
drawPixel(iPartOfNumber(intersectY), x,
rfPartOfNumber(intersectY));
drawPixel(iPartOfNumber(intersectY)-1, x,
fPartOfNumber(intersectY));
intersectY += gradient;
}
}
else
{
int x;
for (x = xpxl1 ; x <=xpxl2 ; x++)
{
// pixel coverage is determined by fractional
// part of y co-ordinate
drawPixel(x, iPartOfNumber(intersectY),
rfPartOfNumber(intersectY));
drawPixel(x, iPartOfNumber(intersectY)-1,
fPartOfNumber(intersectY));
intersectY += gradient;
}
}
}
// Driver code
int main(int argc, char* args[])
{
SDL_Event event;
// initialize SDL
if (SDL_Init(SDL_INIT_EVERYTHING) >= 0)
{
// if succeeded create our window
pWindow = SDL_CreateWindow("Anti-Aliased Line ",
SDL_WINDOWPOS_CENTERED, SDL_WINDOWPOS_CENTERED,
640, 480,
SDL_WINDOW_SHOWN);
// if the window creation succeeded create our renderer
if (pWindow != 0)
pRenderer = SDL_CreateRenderer(pWindow, -1, 0);
}
else
return 1; // sdl could not initialize
while (1)
{
if (SDL_PollEvent(&event) && event.type == SDL_QUIT)
break;
// Sets background color to white
SDL_SetRenderDrawColor(pRenderer, 255, 255, 255, 255);
SDL_RenderClear(pRenderer);
// draws a black AALine
drawAALine(80 , 200 , 550, 150);
// show the window
SDL_RenderPresent(pRenderer);
}
// clean up SDL
SDL_Quit();
return 0;
}
Producción:
Referencias:
https://courses.engr.illinois.edu/ece390/archive/archive-f2000/mp/mp4/anti.html
https://unionassets.com/blog/algorithm-brezenhema-and-wu-s-line -299
https://en.wikipedia.org/wiki/Xiaolin_Wu%27s_line_algorithm
Este artículo es una contribución de Lokesh Sharma . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
