Representación gráfica de datos

En el mundo actual de Internet y la conectividad, hay una gran cantidad de datos disponibles y se necesita algún método u otro para observar grandes datos, los patrones y las tendencias en ellos. Hay una rama completa de las matemáticas dedicada a recopilar, analizar, interpretar y presentar los datos numéricos en forma visual de tal manera que sea fácil de entender y los datos también sean fáciles de comparar, la rama se conoce como Estadísticas . La rama está muy extendida y tiene una gran cantidad de aplicaciones de la vida real, como Business Analytics, demografía, astroestadística, etc. Hay dos formas de representar los datos, 

1. Mesas
2. Representación pictórica a través de gráficos.

Dicen que “una imagen vale más que mil palabras”. Siempre es mejor representar los datos en formato gráfico. Incluso en Pruebas prácticas y encuestas, los científicos han descubierto que la restauración y la comprensión de cualquier información es mejor cuando está disponible en forma de imágenes, ya que los seres humanos procesan los datos mejor en forma visual que en cualquier otra forma. ¿Aumenta la habilidad 2 veces o 3 veces? La respuesta es que aumenta el Poder de comprensión 60.000 veces para un ser Humano normal, el hecho es divertido y cierto al mismo tiempo. Veamos algunos de ellos en detalle. 

Tipos de Representaciones Gráficas

La comparación entre diferentes elementos se muestra mejor con gráficos, se vuelve más fácil comparar el quid de los datos pertenecientes a diferentes elementos. Veamos brevemente todos los diferentes tipos de representaciones gráficas: 

Gráficos de líneas

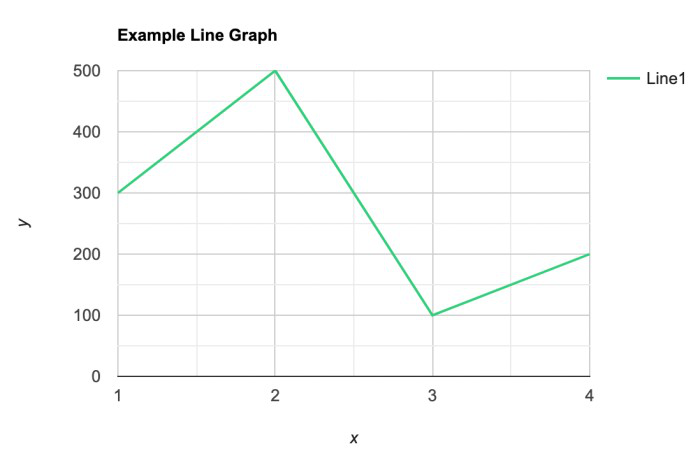
Se utiliza un gráfico de líneas para mostrar cómo cambia el valor de una variable particular con el tiempo. Trazamos este gráfico conectando los puntos en diferentes valores de la variable. Puede ser útil para analizar las tendencias en los datos y predecir futuras tendencias. 

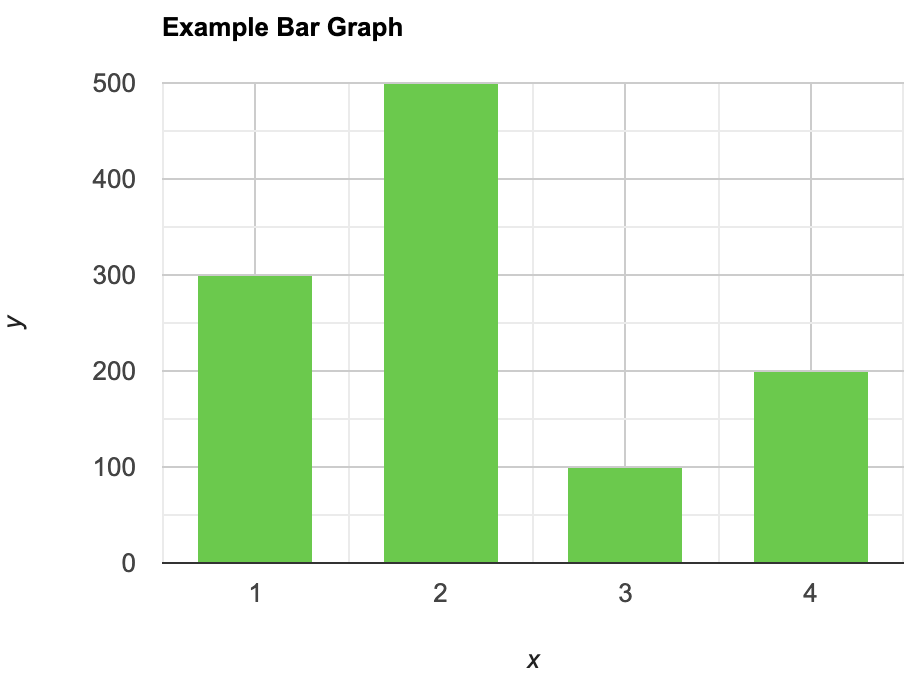
Gráficos de barras

Un gráfico de barras es un tipo de representación gráfica de los datos en el que se dibujan barras de ancho uniforme con el mismo espacio entre ellas en un eje (generalmente el eje x), que representan la variable. Los valores de las variables están representados por la altura de las barras. 

Histogramas 

Esto es similar a los gráficos de barras, pero se basa en la frecuencia de los valores numéricos en lugar de sus valores reales. Los datos están organizados en intervalos y las barras representan la frecuencia de los valores en ese rango. Es decir, cuenta cuántos valores de los datos se encuentran en un rango particular. 

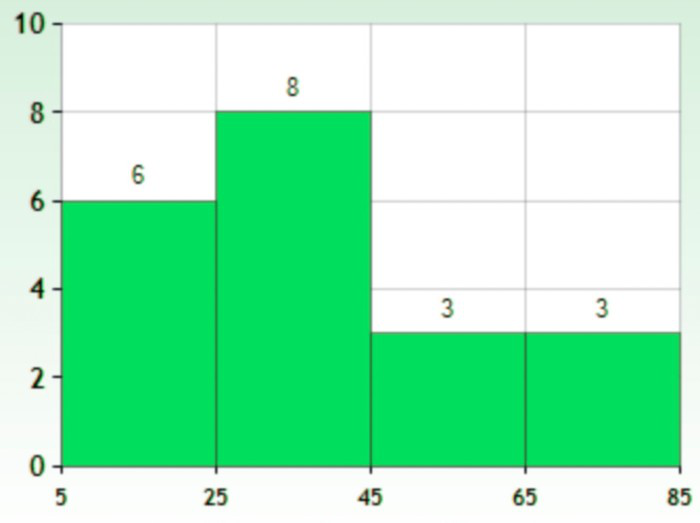
Gráfico de línea 

Es una gráfica que muestra datos como puntos y marcas de verificación sobre una recta numérica, mostrando la frecuencia del punto. 

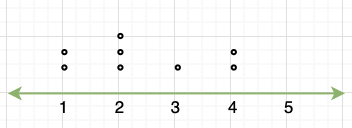
Diagrama de tallo y hoja 

Este es un tipo de gráfico en el que cada valor se divide en una «hoja» (en la mayoría de los casos, es el último dígito) y «tallo» (los otros dígitos restantes). Por ejemplo: el número 42 se divide en hoja (2) y tallo (4).  

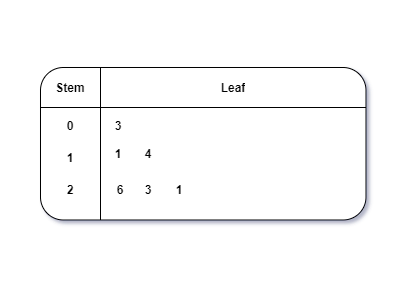
Diagrama de caja y bigotes 

Estos gráficos dividen los datos en cuatro partes para mostrar su resumen. Están más preocupados por la dispersión, el promedio y la mediana de los datos. 

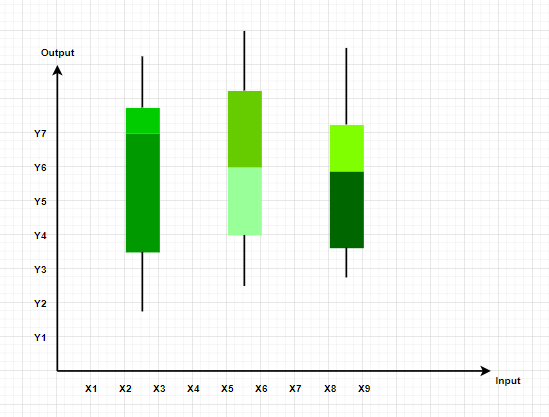
Gráfico circular

Es un tipo de gráfico que representa los datos en forma de un gráfico circular. El círculo se divide de manera que cada porción representa una proporción del todo. 

Representaciones gráficas utilizadas en matemáticas

Los gráficos en matemáticas se utilizan para estudiar las relaciones entre dos o más variables que están cambiando. Los datos estadísticos se pueden resumir de una mejor manera usando gráficos. Básicamente, hay dos líneas de pensamiento para hacer gráficos en matemáticas: 

1. Gráficos de series temporales o basados ​​en valores
2. Basado en frecuencia

Gráficos de series temporales o basados ​​en valores 

Estos gráficos nos permiten estudiar el cambio de una variable con respecto a otra variable dentro de un intervalo de tiempo determinado. Las variables pueden ser cualquier cosa. Los gráficos de Serie Temporal estudian el cambio de variable con el tiempo. Estudian las tendencias, el comportamiento periódico y los patrones de la serie. Aquí nos preocupan más los valores de las variables que la frecuencia de esos valores. 

Ejemplo: gráfico de líneas

Basado en frecuencia

Este tipo de gráficos están más preocupados por la distribución de datos. Cuántos valores se encuentran entre un rango particular de las variables y qué rango tiene la frecuencia máxima de los valores. Se utilizan para juzgar una extensión y un promedio y, a veces, una mediana de una variable en estudio. 

Ejemplo: Polígono de frecuencias, Histogramas.

Principios de las Representaciones Gráficas

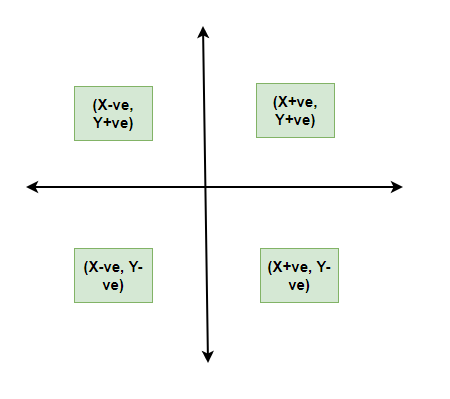
Todos los tipos de representaciones gráficas requieren algunas reglas/principios que deben seguirse. Estos son algunos principios algebraicos. Cuando trazamos un gráfico, hay un origen y tenemos nuestros dos ejes. Estos dos ejes dividen el plano en cuatro partes llamadas cuadrantes. El horizontal generalmente se llama eje x y el otro se llama eje y. El origen es el punto donde estos dos ejes se cruzan. Lo que debemos tener en cuenta acerca de los valores de la variable en el eje x es que los valores positivos deben estar en el lado derecho del origen y los valores negativos deben estar en el lado izquierdo del origen. De manera similar, para la variable en el eje y, debemos asegurarnos de que los valores positivos de esta variable deben estar por encima del eje x y los valores negativos de esta variable deben estar por debajo del eje y. 

Ventajas y desventajas de usar el sistema gráfico

ventajas: 

1. Nos da un resumen de los datos que es más fácil de ver y analizar.
2. Ahorra tiempo.
3. Podemos comparar y estudiar más de una variable a la vez.

Desventaja: 

Por lo general, toma solo un aspecto de los datos e ignora el otro. Por ejemplo, un gráfico de barras no representa la media, la mediana y otras estadísticas de los datos. 

Reglas Generales para la Representación Gráfica de Datos

Debemos tener en cuenta algunas cosas al trazar y diseñar estos gráficos. El objetivo debe ser una imagen mejor y más clara de los datos. Se deben tener en cuenta las siguientes cosas al trazar los gráficos anteriores: 

1. Siempre que sea posible, se debe mencionar la fuente de datos para el espectador.
2. Elija siempre los colores y tamaños de fuente adecuados. Deben elegirse teniendo en cuenta que los gráficos deben verse limpios.
3. La Unidad de medida debe mencionarse en la esquina superior derecha del gráfico.
4. Se debe elegir la escala adecuada al hacer el gráfico, se debe elegir de tal manera que el gráfico se vea preciso.
5. Por último, pero no menos importante, se debe elegir un título adecuado.

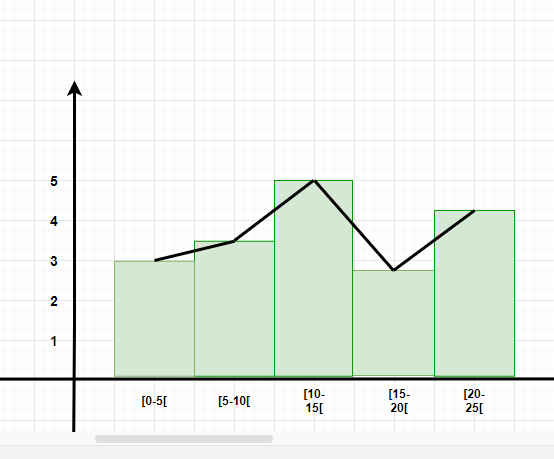
Polígono de frecuencia

Un polígono de frecuencias es un gráfico que se construye uniendo el punto medio de los intervalos. La altura del intervalo o bin representa la frecuencia de los valores que se encuentran en ese intervalo. 

Problemas de muestra

Pregunta 1: ¿Cuáles son los diferentes tipos de gráficas basadas en frecuencia? 

Responder: 

Tipos de gráficas basadas en frecuencia: 

1. Histograma
2. Polígono de frecuencia
3. Diagramas de caja

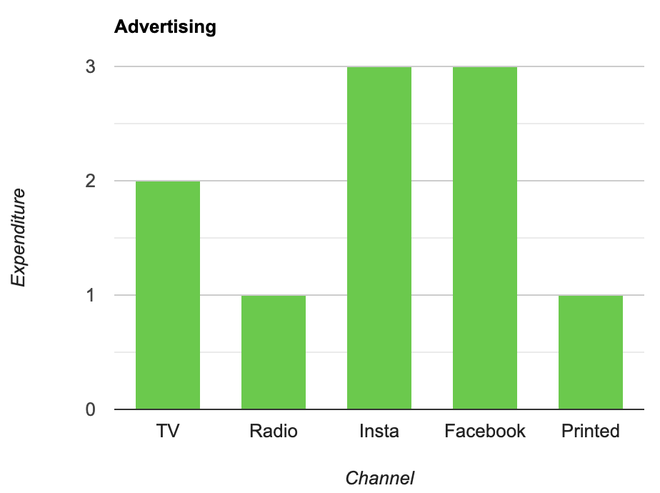
Pregunta 2: Una empresa con un presupuesto publicitario de Rs 10,00,00,000 ha planificado los siguientes gastos en los diferentes canales publicitarios, como publicidad televisiva, radio, Facebook, Instagram y medios impresos. La tabla representa el dinero gastado en diferentes canales. 

Canal de publicidad	Gastos (en millones de rupias)
Anuncio de televisión	2
Radio	1
Facebook	3
Instagram	3
Medios impresos	1

Dibuja un gráfico de barras para los siguientes datos. 

Solución: 

Pasos: 

1. Coloque cada uno de los canales en el eje x
2. La altura de las barras se decide por el valor de cada canal.

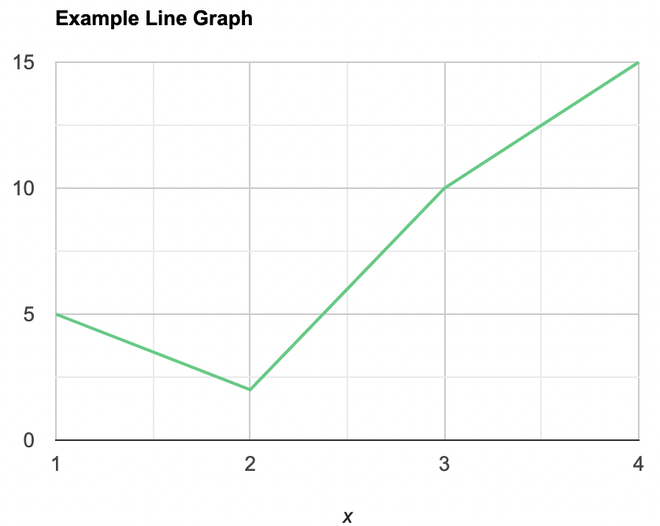
Pregunta 3: Dibuja un diagrama de puntos para los siguientes datos 

X	1	2	3	4	5	6
y	5	2	10	15	12	8

Solución:

Pasos: 

1. Coloque cada uno de los valores de la fila del eje x en el eje x
2. conjunta el valor correspondiente a cada valor del eje x.

Pregunta 4: Haz una gráfica de frecuencia de los siguientes datos: 

X	[0-3]	[3-16]	[6-9]	[9-12]
y	3	4	2	6

Solución: 

Pasos: 

1. Dibuja los intervalos de clase en el eje x y las frecuencias en el eje y.
2. Calcular el punto medio de cada intervalo de clase.

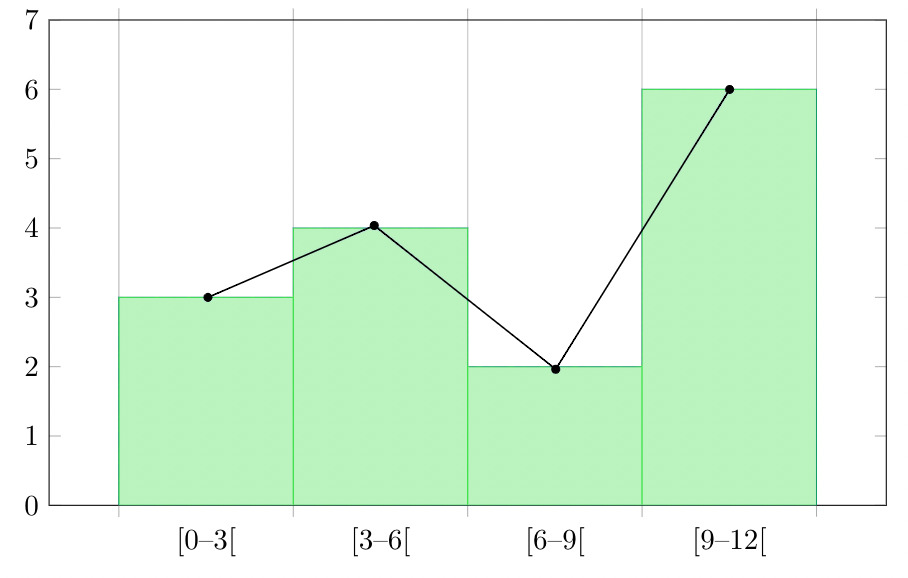
Intervalo de clases	punto medio	Frecuencia
0-3	1.5	3
3-6	4.5	4
6-9	7.5	2
9-12	10.5	6

Ahora une los puntos medios de los intervalos y sus correspondientes frecuencias en el gráfico. 

Este gráfico muestra tanto el histograma como el polígono de frecuencias para la distribución dada.