No hace falta decir que, en general, un motor de búsqueda responde a una consulta determinada con una lista clasificada de documentos relevantes. El propósito de este artículo es describir un primer enfoque para encontrar documentos relevantes con respecto a una consulta determinada. En el modelo de espacio vectorial (VSM), cada documento o consulta es un vector N-dimensional donde N es el número de términos distintos sobre todos los documentos y consultas. El i-ésimo índice de un vector contiene la puntuación del i-ésimo término para ese vector.
Las principales funciones de puntuación se basan en: Term-Frequency (tf) y Inverse-Document-Frequency (idf).
Frecuencia de término y frecuencia de documento inversa: la frecuencia
de término ( ![]() ) se calcula con respecto al i-ésimo término y al j-ésimo documento:
) se calcula con respecto al i-ésimo término y al j-ésimo documento:
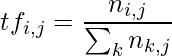
donde ![]() están las apariciones del i-ésimo término en el j-ésimo documento.
están las apariciones del i-ésimo término en el j-ésimo documento.
La idea es que si un documento tiene múltiples recepciones de términos dados, probablemente tratará con ese argumento.
La Frecuencia-Documento-Inversa ( ![]() ) toma en consideración los i-ésimos términos y todos los documentos en la colección:
) toma en consideración los i-ésimos términos y todos los documentos en la colección:

La intuición es que los términos raros son más importantes que los comunes: si un término está presente solo en un documento, puede significar que el término caracteriza ese documento.
La puntuación final ![]() del término i-ésimo en el documento j-ésimo consiste en una simple multiplicación:
del término i-ésimo en el documento j-ésimo consiste en una simple multiplicación: ![]() . Dado que un documento/consulta contiene solo un subconjunto de todos los términos distintos de la colección, la frecuencia de términos puede ser cero para una gran cantidad de términos: esto significa que se necesita una representación vectorial dispersa para optimizar los requisitos de espacio.
. Dado que un documento/consulta contiene solo un subconjunto de todos los términos distintos de la colección, la frecuencia de términos puede ser cero para una gran cantidad de términos: esto significa que se necesita una representación vectorial dispersa para optimizar los requisitos de espacio.
Similitud del coseno:
para calcular la similitud entre dos vectores: a, b (documento/consulta pero también documento/documento), se utiliza la similitud del coseno:

Esta fórmula calcula el coseno del ángulo descrito por los dos vectores normalizados: si los vectores están cerca, el ángulo es pequeño y la relevancia es alta.
Se puede demostrar que la similitud del coseno es la misma que la distancia euclidiana bajo el supuesto de normalización vectorial.
Mejoras:
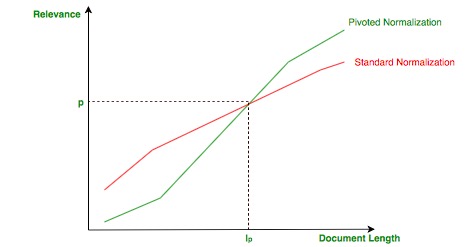
hay un problema sutil con la normalización de vectores: los documentos cortos que hablan de un solo tema pueden verse favorecidos a expensas de los documentos largos que tratan más temas porque la normalización no tiene en cuenta la longitud de un documento.
La idea de la normalización dinámica es hacer que el documento sea más corto que un valor empírico (longitud dinámica:) ![]() menos relevante y el documento más largo sea más relevante, como se muestra en la siguiente imagen: Normalización dinámica
menos relevante y el documento más largo sea más relevante, como se muestra en la siguiente imagen: Normalización dinámica
Un gran problema que no se tiene en cuenta en el VSM son los sinónimos: no hay relación semántica entre los términos, ya que no se captura ni en la frecuencia del término ni en la frecuencia inversa del documento. Para resolver estos problemas se ha introducido el Modelo Generalizado de Espacio Vectorial (GVSM).
Publicación traducida automáticamente
Artículo escrito por AngeloCatalani y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA