La media es el promedio de un conjunto dado de datos. Consideremos a continuación el ejemplo 2, 4, 4, 4, 5, 5, 7, 9, la media (promedio) de un conjunto dado de datos es 5 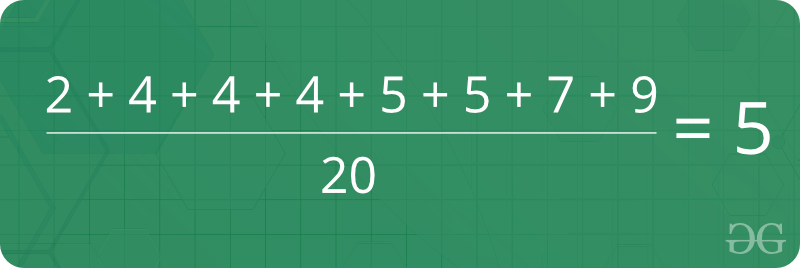 Hecho sobre la media:
Hecho sobre la media:
- La media (o promedio) es la medida de tendencia central más popular y conocida.
- Puede usarse tanto con datos discretos como continuos, aunque su uso es más frecuente con datos continuos.
- Existen otros tipos de medias. Media geométrica, Media armónica y Media aritmética.
- La media es la única medida de tendencia central donde la suma de las desviaciones de cada valor de la media es siempre cero.
Fórmula de la media de datos no agrupados: 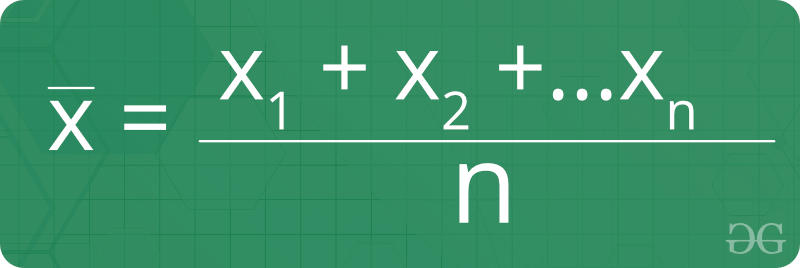 Fórmula de la media de datos agrupados:
Fórmula de la media de datos agrupados:  ¿Cómo encontrar la media? Dada una array no ordenada de tamaño n , encuentre su media.
¿Cómo encontrar la media? Dada una array no ordenada de tamaño n , encuentre su media.
Media de una array = (suma de todos los elementos) / (número de elementos) Dado que la array no está ordenada aquí, primero ordenamos la array y luego aplicamos la fórmula anterior.
Ejemplos:
Input : {1, 3, 4, 2, 6, 5, 8, 7}
Output : Mean = 4.5
Sum of the elements is 1 + 3 + 4 + 2 + 6 +
5 + 8 + 7 = 36
Mean = 36/8 = 4.5
Input : {4, 4, 4, 4, 4}
Output : Mean = 4
A continuación se muestra la implementación del código:
C++
// CPP program to find mean
#include <bits/stdc++.h>
using namespace std;
// Function for calculating mean
double findMean(int a[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
return (double)sum / (double)n;
}
// Driver program
int main()
{
int a[] = { 1, 3, 4, 2, 7, 5, 8, 6 };
int n = sizeof(a) / sizeof(a[0]);
cout << "Mean = " << findMean(a, n) << endl;
return 0;
}
Java
// Java program to find mean
import java.util.*;
class GFG {
// Function for calculating mean
public static double findMean(int a[], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
return (double)sum / (double)n;
}
// Driver program
public static void main(String args[])
{
int a[] = { 1, 3, 4, 2, 7, 5, 8, 6 };
int n = a.length;
System.out.println("Mean = " + findMean(a, n));
}
}
Python3
# Python3 program to find mean
# Function for calculating mean
def findMean(a, n):
sum = 0
for i in range( 0, n):
sum += a[i]
return float(sum / n)
# Driver program
a = [ 1, 3, 4, 2, 7, 5, 8, 6 ]
n = len(a)
print("Mean =", findMean(a, n))
C#
// C# program to find mean
using System;
class GFG {
// Function for
// calculating mean
public static double findMean(int[] a, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += a[i];
return (double)sum / (double)n;
}
// Driver Code
public static void Main()
{
int[] a = { 1, 3, 4, 2,
7, 5, 8, 6 };
int n = a.Length;
Console.Write("Mean = " + findMean(a, n) + "\n");
}
}
PHP
<?php
// PHP program to find mean
// Function for calculating mean
function findMean(&$a, $n)
{
$sum = 0;
for ($i = 0; $i < $n; $i++)
$sum += $a[$i];
return (double)$sum /
(double)$n;
}
// Driver Code
$a = array(1, 3, 4, 2,
7, 5, 8, 6);
$n = sizeof($a);
echo "Mean = " .
findMean($a, $n)."\n";
?>
Producción:
Mean = 4.5
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(1)
Programa básico relacionado con la media
- Encuentra la media de las medias de los subarreglos en una array dada
- Media de array usando recursividad
- Encuentra el vector medio de una array
- Media de rango en array
- Media y mediana de una array
Artículos recientes sobre Mean!
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA