Explicabilidad del aprendizaje automático mediante la importancia de la permutación

Los modelos de aprendizaje automático a menudo actúan como cajas negras, lo que significa que pueden hacer buenas predicciones, pero es difícil comprender completamente las decisiones que impulsan esas predicciones. Obtener información de un modelo no es una tarea fácil, a pesar de que pueden ayudar con la depuración, la ingeniería de características, la dirección de la recopilación de datos futuros, la toma de decisiones informada y, finalmente, generar confianza en las predicciones de un modelo.

Una de las consultas más triviales con respecto a un modelo podría ser determinar qué características tienen el mayor impacto en las predicciones, lo que se denomina importancia de características . Una forma de evaluar esta métrica es la importancia de la permutación . 

La importancia de la permutación se calcula una vez que se ha entrenado un modelo en el conjunto de entrenamiento. Pregunta: si los puntos de datos de un solo atributo se barajan aleatoriamente (en el conjunto de validación), dejando todos los datos restantes como están, ¿cuáles serían las ramificaciones en la precisión usando estos nuevos datos?

Idealmente, el reordenamiento aleatorio de una columna debería dar como resultado una precisión reducida, ya que los nuevos datos tienen poca o ninguna correlación con las estadísticas del mundo real. La precisión del modelo sufre más cuando se baraja una característica importante de la que el modelo dependía bastante. Con esta idea, el proceso es el siguiente:

1. Consigue un modelo entrenado.
2. Mezcla los valores de un solo atributo y utiliza estos datos para obtener nuevas predicciones. A continuación, evalúe el cambio en la función de pérdida utilizando estos nuevos valores y predicciones para determinar el efecto de la barajada. La caída en el rendimiento cuantifica la importancia de la función que se ha barajado.
3. Invierta la mezcla realizada en el paso anterior para recuperar los datos originales. Vuelva a realizar el paso 2 utilizando el siguiente atributo, hasta que se determine la importancia de cada característica.

La biblioteca ELI5 de Python proporciona una forma conveniente de calcular la importancia de la permutación. Funciona en Python 2.7 y Python 3.4+. Actualmente requiere scikit-learn 0.18+. Puede instalar ELI5 usando pip:

pip install eli5

o usando:

conda install -c conda-forge eli5

Entrenaremos un regresor de bosque aleatorio usando el conjunto de datos de precios de vivienda de Boston de scikitlearn y usaremos ese modelo entrenado para calcular la importancia de la permutación.

Cargar conjunto de datos

from sklearn.datasets import load_boston
  
boston = load_boston()
print(boston.DESCR[20:1420])

Producción:

Dividir en conjuntos de entrenamiento y prueba

from sklearn.model_selection import train_test_split
  
# separate data into target & independent variables
x = boston.data
y = boston.target
  
# split data into train and test set
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8)
print('Size of: ')
print('Training Set x: ', x_train.shape)
print('Training Set y: ', y_train.shape)
print('Test Set x: ', x_test.shape)
print('Test Set y: ', y_test.shape)

Producción:

Size of: 
Training Set x: (404, 13)
Training Set y: (404,)
Test Set x: (102, 13)
Test Set y: (102,)

modelo de tren

from sklearn.ensemble import RandomForestRegressor
  
# train model on training set
rf = RandomForestRegressor()
  
# fit model on training set
rf.fit(x_train, y_train)
  
# calculate score on test set
print('R2 score for test set: ')
print(rf.score(x_test, y_test))

Producción:

R2 score for test set: 0.857883705095584

Evaluar la importancia de la permutación

import eli5
from eli5.sklearn import PermutationImportance
  
# create permutation importance object using model
# and fit on test set
perm = PermutationImportance(rf, random_state=1).fit(x_test, y_test)
  
# display weights using PermutationImportance object
eli5.show_weights(perm, feature_names = boston.feature_names)

Producción:

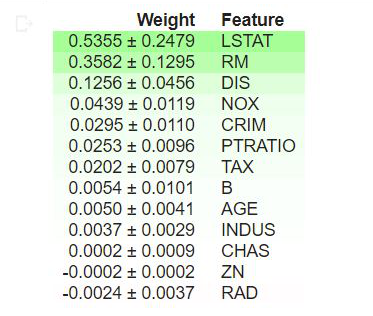
Interpretación

• Los valores en la parte superior de la tabla son las características más importantes de nuestro modelo, mientras que los de la parte inferior son los que menos importan.
• El primer número de cada fila indica cuánto disminuyó el rendimiento del modelo con la mezcla aleatoria, utilizando la misma métrica de rendimiento que el modelo (en este caso, la puntuación R2).
• El número después de ± mide cómo varió el rendimiento de una reorganización a la siguiente, es decir, el grado de aleatoriedad en múltiples reorganizaciones.
• Los valores negativos para la importancia de la permutación indican que las predicciones sobre los datos mezclados (o ruidosos) son más precisas que los datos reales. Esto significa que la característica no contribuye mucho a las predicciones (importancia cercana a 0), pero la probabilidad aleatoria hizo que las predicciones sobre los datos mezclados fueran más precisas. Esto es más común con pequeños conjuntos de datos.

En nuestro ejemplo, las 3 características principales son LSTAT, RM y DIS, mientras que las 3 menos significativas son RAD, CHAS y ZN.

Resumen

Este artículo es una breve introducción a la explicabilidad del aprendizaje automático mediante la importancia de la permutación en Python. Obtener intuición sobre el impacto de las características en el rendimiento de un modelo puede ayudar con la depuración y proporcionar información sobre el conjunto de datos, lo que lo convierte en una herramienta útil para los científicos de datos.

Referencias

1. Documentación ELI5
2. Curso de explicabilidad del aprendizaje automático de Kaggle
3. RandomForestRegressor de Sklearn
4. Conjunto de datos de precios de vivienda de Boston