Clase 10 Soluciones RD Sharma – Capítulo 9 Progresiones aritméticas – Ejercicio 9.6 | Serie 1

Pregunta 1. Encuentra la suma de las siguientes progresiones aritméticas:

(i) 50, 46, 42, … a 10 términos

Solución: 

Dado que AP tiene el primer término (a) = 50, 

Diferencia común(d) = 46 – 50 = – 4 

y número de términos (n) = 10

Entonces, Suma de AP = S ₁₀ = n[2a + (n – 1)d] / 2

= 10[2(50) + (10 – 1)(-4)]/2

= (10)(100 – 36)/2 

= 320

Por lo tanto, la suma de los primeros 10 términos de AP es 320.

(ii) 1, 3, 5, 7, …..a 12 términos.

Solución: 

Dado que AP tiene el primer término (a) = 1, 

diferencia común (d) = 3 – 1 = 2 

y número de términos (n) = 12

Entonces, Suma de AP = S ₁₂ = n[2a + (n – 1)d] / 2

= 12[2(1) + (12 – 1)(2)]/2

= 12[2 + 22]/2 

= 144

Por lo tanto, la suma de los primeros 12 términos de AP es 144.

(iii) 3, 9/2, 6, 15/2, … a 25 términos

Solución: 

Dado que AP tiene el primer término (a) = 3, 

Diferencia común (d) = 9/2 – 3 = 3/2 

y número de términos (n) = 25

Entonces, Suma de AP = S ₂₅ = n[2a + (n – 1)d] / 2

= 25[2(3) + (25 – 1)(3/2)]/2

= 25[6 + 36]/2 = 525

Por lo tanto, la suma de los primeros 25 términos de AP es 525.

(iv) 41, 36, 31, ….. a 12 términos.

Solución: 

Dado que AP tiene el primer término (a) = 41, 

Diferencia común (d) = 36 – 41 = -5 

y número de términos (n) = 12

Entonces, Suma de AP = S ₁₂ = n[2a + (n – 1)d] / 2

= 12[2(41) + (12 – 1)(-5)]/2

= 12[82 – 55] = 162

Por lo tanto, la suma de los primeros 12 términos de AP es 162.

(v) a + b, a – b, a – 3b, ….. a 22 términos

Solución:

Dado que AP tiene el primer término (a) = a + b, 

Diferencia común(d) = (a – b) – (a + b) = -2b 

y número de términos (n) = 22

Entonces, Suma de AP = S ₂₂ = n[2a + (n – 1)d] / 2

= 22[2(a + b) + (22 – 1)(-2b)]/2

= 11{2(a + b) – 22b)

= 11(2a – 40b) = 22a – 440b

Por tanto, la suma de los primeros 22 términos de AP es 22a – 440b.

(vi) (x – y) ² ,(x ² + y ² ), (x + y) ² ,… a n términos

Solución:

Dado que AP tiene el primer término (a) = (x – y) ² , 

número de términos(n) = n y

Diferencia común(d) = x ² + y ² – (x – y) ² = x ² + y ² – x ² + y ² + 2xy = 2xy

Entonces, Suma de AP = S _n = n[2a + (n – 1)d] / 2

= n[2(x – y) ² +(n – 1)(2xy)]/2

= n[(x – y) ² +(n – 1)(xy)]

Por lo tanto, la suma de los primeros n términos de AP es n[(x – y) ² +(n – 1)(xy)].

(vii)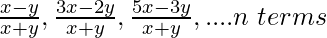 

Solución:

Dado que AP tiene el primer término (a) = 

número de términos(n) = n y

Diferencia común(d) =         

=         

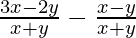
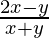
Entonces, Suma de AP = S _n = n[2a + (n – 1)d] / 2

= 

= 

= 

Por lo tanto, la suma de los primeros n términos de AP es 

(viii) –26, –24, –22,…. a 36 términos

Solución:

Dado que AP tiene el primer término (a) = -26, 

Diferencia común(d) = -24 – (-26) = 2 

y número de términos (n) = n.

Entonces, Suma de AP = S ₃₆ = n[2a + (n – 1)d] / 2

= 36[2(-26) + (36 – 1)2]/2

= 18[-52 + 70] = 324

Por lo tanto, la suma de los primeros 36 términos de AP es 324.

Pregunta 2. Encuentra la suma en n términos de AP 5, 2, –1, – 4, –7, …

Solución:

Dado que AP tiene el primer término (a) = 5, 

Diferencia común (d) = 2 – 5 = -3

Suma de n términos de AP = S _n = n[2a + (n – 1)d] / 2

= n[2(5) + (n – 1)(-3)] / 2

= n{10 – 3n + 3)} / 2 

= n / 2(13 – 3n)

Por tanto, la suma de los n términos de AP es n/2(13 – 3n).

Pregunta 3. Encuentra la suma de n términos de un AP cuyos términos están dados por a _n = 5 – 6n.

Solución:

Dado que AP tiene n-ésimo término, an = 5 – 6n

Poniendo n = 1, obtenemos un primer término de la AP,

a = 5 – 6(1) = -1

Suma de n términos de AP = S _n = n[a + an]/2

= n[-1 + (5 – 6n)]/2

= n(4 – 6n)/2 = n(2 – 3n)

Por tanto, la suma de los n términos de AP es n(2 – 3n).

Pregunta 4. Encuentra la suma de los últimos diez términos del AP: 8, 10, 12, 14, .. , 126.

Solución:

Dado que AP tiene el primer término (a) = 8, 

Diferencia común (d) = 10 – 8 = 2 

y enésimo término (a _n ) = 126.

El n-ésimo término del AP está dado por, a _n = a+(n – 1)d

=> 126 = 8 + (n – 1)(2)

=> 126 = 8 + 2n – 2

=> 2n = 120

=> norte = 60

Tenemos que encontrar la suma de los últimos diez términos, es decir,

S = un ₅₁ + un ₅₂ + un ₅₃ + ……. + un ₆₀

51 = 8 + (51 – 1)(2) = ₈ + 50(2) = 108

Entonces, la suma sería S = 10[108 + 126]/2 = 5(234) = 1170

Por lo tanto, la suma de los últimos 10 términos del AP es 1170.

Pregunta 5. Encuentra la suma de los primeros 15 términos de cada una de las siguientes secuencias que tienen el término n como:

(i) un _n = 3 + 4n

Solución:

Dado que AP tiene n-ésimo término, a _n = 3 + 4n 

y número de términos (n) = 15

Entonces, un _n = 3 + 4(15) = 63

Al poner n = 1, obtenemos un primer término de la AP,

a = 3 + 4(1) = 7

S ₁₅ = n[a + a _n ]/2

= 15(7 + 63)/2 = 15×35 = 525

Por lo tanto, la suma de los primeros 15 términos de AP dado es 525.

(ii) bn ₌ 5 + 2n

Solución:

Dado que AP tiene n-ésimo término, a _n = 5 + 2n y 

número de términos (n) = 15

Entonces, _n = 5 + 2(15) = 35

Al poner n = 1, obtenemos un primer término de la AP,

a = 5 + 2(1) = 7

S ₁₅ = n[a + a _n ]/2

= 15(7 + 35)/2 = 15×21 = 315

Por lo tanto, la suma de los primeros 15 términos de AP dado es 315.

(iii) x _n = 6 – n

Solución:

Dado que AP tiene n-ésimo término, a _n = 6 – n 

y número de términos (n) = 15

Entonces, un _n = 6 – n = -9

Al poner n = 1, obtenemos un primer término de la AP,

a = 6 – 1 = 5

S ₁₅ = n[a + a _n ]/2

= 15(5 – 9)/2 = 15 x (-2) = -30

Por lo tanto, la suma de los primeros 15 términos de AP dado es -30.

(iv) _yn = 9 – 5n

Solución:

Dado que AP tiene n-ésimo término, a _n = 9 – 5n 

y número de términos (n) = 15

Entonces, a _n = 9 – 5(15) = -66

Al poner n = 1, obtenemos un primer término de la AP,

un = 9 – 5 = 4

S ₁₅ = n[a + a _n ]/2

= 15(4 – 66)/2 = 15 x (-31) = -465

Por tanto, la suma de los primeros 15 términos de AP dado es -465.

Pregunta 6. Halla la suma de los primeros 20 términos de la sucesión cuyo enésimo término es a _n = An + B.

Solución:

Dado que AP tiene n-ésimo término, a _n = An + B 

y número de términos (n) = 20

Entonces, un _n = A(20) + B = 20A + B

Al poner n = 1, obtenemos un primer término de la AP,

a = A(1) + B = A + B

S ₂₀ = n[a + a _n ]/2

= 20(A+B+20A+B)/2

= 10[21A + 2B]

= 210A + 20B

Por tanto, la suma de los primeros 20 términos de AP dado es 210A + 20B.

Pregunta 7. Halla la suma de los primeros 25 términos de un AP cuyo enésimo término está dado por a _n = 2 – 3n.

Solución:

Dado que AP tiene n-ésimo término, a _n = 2 – 3n 

y número de términos (n) = 25

Entonces, un _n = 2 – 3(25) = -73

Al poner n = 1, obtenemos un primer término de la AP,

a = 2 – 3(1) = -1

S ₂₀ = n[a + a _n ]/2

= 25(-1 – 73)/2

= 25 x (-37) = -925

Por tanto, la suma de los primeros 25 términos de AP dado es -925.

Pregunta 8. Encuentra la suma de los primeros 25 términos de un AP cuyo n-ésimo término está dado por a _n = 7 – 3n.  

Solución:

Dado que AP tiene n-ésimo término, a _n = 7 – 3n 

y número de términos (n) = 25

Entonces, a _n = 7 – 3(25) = -68

Al poner n = 1, obtenemos un primer término de la AP,

a = 7 – 3(1) = 4

S ₂₅ = norte[un + un _norte ]/2

= 25(4 – 68)/2

= 25 × (-32)

= -800

Por tanto, la suma de los primeros 25 términos de AP dado es -800.

Pregunta 9. Si la suma de cierto número de términos a partir del primer término de un AP es 25, 22, 19, . . ., es 116. Encuentra el último término.

Solución:

Dado que AP tiene el primer término (a) = 25, 

Diferencia común (d) = 22 – 25 = -3 y suma (S _n ) = 116.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n – 1)d] / 2.

=> 116 = n[2(25) + (n − 1)(−3)]/2

=> n[53 − 3n]/2 = 116

=> 53n – 3n ² = 232

=> 3n ² – 53n + 232 = 0

=> 3n ² – 24n – 29n + 232 = 0

=> 3n(n-8)-29 (n-8) = 0

=> (3n – 29)(n – 8) = 0

=> n = 29/3 o n = 8

Ignorando n = 29/3 como número de términos no puede ser una fracción, entonces obtenemos n = 8.

Entonces, el último término es:

a ₈ = a + (8 – 1)d = 25 + 7(-3) = 25 – 21 = 4

Por lo tanto, el último término del AP dado es 4.

Pregunta 10 (i). ¿Cuántos términos de la sucesión 18, 16, 14…. deben tomarse de modo que su suma sea cero.  

Solución:

Dado que AP tiene el primer término (a) = 18, 

Diferencia común(d) = 16 – 18 = -2 y suma(S _n ) = 0.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n – 1)d] / 2.

=> 0 = n[2(18) + (n – 1)(-2)]/2

=> 0 = n[36 + (-2n + 2)]/2

=> n[38 − 2n] = 0

=> n = 0 o 38 – 2n = 0

Ignorando n = 0 como número de términos no puede ser 0. Entonces obtenemos,

=> 38 – 2n = 0

=> 2n = 38

=> norte = 19

Por lo tanto, el número de términos (n) es 19.

(ii) ¿Cuántos términos hay en el AP cuyo primer y quinto términos son -14 y 2 respectivamente y la suma de los términos es 40?

Solución:

Dado que AP tiene el primer término (a) = –14, 

Quinto término(a ₅ ) = 2 y suma(S _n ) = 40.

Sea la diferencia común de los AP d. Obtenemos,

Entonces, a ₅ = a + (5 – 1)d

=> 2 = -14 + 4d

=> 4d = 16

=> re = 4

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n – 1)d] / 2.

=> 40 = n[2(-14) + (n – 1)(4)]/2

=> 40 = n[-28 + (4n – 4)]/2

=> 40 = n[-32 + 4n]/2

=> 4n ² – 32n – 80 = 0

=> n ² – 8n – 20 = 0

=> n ² -10n + 2n – 20 = 0

=> n(n -10) + 2(n – 10 ) = 0

=> (n + 2)(n – 10) = 0

=> n = -2 o n = 10

Ignorar n = -2 como número de términos no puede ser negativo. Entonces obtenemos, n = 10.

Por lo tanto, el número de términos (n) es 10.

( iii) ¿Cuántos términos del AP 9, 17, 25, . . . deben tomarse para que su suma sea 636?

Solución:

Dado que AP tiene el primer término (a) = 9, 

Diferencia común(d) = 17 – 9 = 8 y suma(S _n ) = 636.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n – 1)d] / 2.

=> 636 = n[2(9) + (n − 1)(8)]/2

=> 636 = n[18 + (8n − 8)]/2

=>1271 = 10n + 8n ²

=> 8n ² + 10n − 1272 = 0

=> 4n ² + 5n − 636 = 0

=> 4n ² − 48n + 53n − 636 = 0

=> 4n(n − 12) + 53(n − 12) = 0

=> (4n + 53)(n − 12) = 0

=> n = −53/4 o n = 12

Ignorando n = −53/4 como número de términos no puede ser una fracción. Entonces obtenemos, n = 12.

Por lo tanto, el número de términos (n) es 12.

(iv) ¿Cuántos términos del AP 63, 60, 57, . . . deben tomarse para que su suma sea 693?

Solución:

Dado que AP tiene el primer término (a) = 63, 

Diferencia común(d) = 60 – 63 = -3 y suma(S _n ) = 636.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n – 1)d] / 2.

=> 693 = n[2(63) + (n − 1)(−3)]/2

=> 693 = n[126+(−3n + 3)]/2

=> 693 = n[129 − 3n]/2

=> 129n − 3n ² = 1386

=> 3n ² − 129n + 1386 = 0

=> norte ² − 43n + 462 = 0

=> norte ² − 22n − 21n + 462 = 0

=> n(n − 22) − 21(n − 22) = 0

=> (n −22) (n −21) = 0

=> n = 22 o n = 21

Entonces, el valor de n puede ser tanto 21 como 22 porque,

un ₂₂ = un + 21d = 63 + 21(− 3) = 63 − 63 = 0

La suma sigue siendo la misma incluso si agregamos el término 22 porque su valor es 0.

Por lo tanto, el número de términos (n) es 21 o 22.

(v) ¿Cuántos términos del AP son 27, 24, 21. . . debe tomarse que su suma es cero?

Solución:

Dado que AP tiene el primer término (a) = 27, 

diferencia común(d) = 24 − 27 = −3 

y suma(Sn ₎ = 0.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

=> 0 = n[2(27) + (n − 1)( − 3)]/2

=> 0 = n[54 + (n − 1)(-3)]

=> 0 = n[54 − 3n + 3]

=> n[57 − 3n] = 0

=> n = 0 o 3n = 57

Ignorando n = 0 como número de términos no puede ser cero. Entonces obtenemos,

=> 3n = 57

=> norte = 19

Por lo tanto, el número de términos (n) es 19.

Pregunta 11. Halla la suma de los primeros

(i) 11 términos del AP: 2, 6, 10, 14, . . .

Solución:

Dado que AP tiene el primer término (a) = 2, 

Diferencia común(d) = 6 − 2 = 4 

y número de términos (n) = 11.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

S ₁₁ = 11[2(2) + (11 − 1)4]/2

= 11[4 + 40]/2

= 11 × 22 = 242

Por lo tanto, la suma de los primeros 11 términos del AP dado es 242.

(ii) 13 términos del AP: -6, 0, 6, 12, . . .

Solución:

Dado que AP tiene el primer término (a) = -6, 

Diferencia común(d) = 0 − (−6) = 6 

y número de términos (n) = 13.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

S ₁₃ = 13[2(−6) + (13 − 1)6]/2

= 13[(−12) + 72]/2

= 13[30] = 390

Por lo tanto, la suma de los primeros 13 términos del AP dado es 390.

(iii) 51 términos del AP: cuyo segundo término es 2 y cuarto término es 8.

Solución:

Dado que AP tiene un segundo término (a ₂ ) = 2, 

Cuarto término(a ₄ ) = 8 y 

número de términos (n) = 51.

=> un ₂ = un + re

=> 2 = a + d …(1)

Además, un ₄ = un + 3d

=> 8 = a + 3d … (2)

Restando (1) de (2), tenemos

=> 2d = 6

=> re = 3

Poniendo d = 3 en (1), obtenemos a = −1.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

S ₅₁ = 51[2(−1) + (51 − 1)(3)]/2

= 51[−2 + 150]/2

= 51[74] = 3774

Por lo tanto, la suma de los primeros 51 términos del AP dado es 3774.

Pregunta 12. Encuentra la suma de

(i) los primeros 15 múltiplos de 8

Solución:

Los primeros 15 múltiplos de 8 son 8, 16, 24, …… , 120.

Estos múltiplos forman un AP con el primer término (a) = 8, 

Diferencia común(d) = 16 − 8 = 8 

y número de términos (n) = 15.

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

S ₁₅ = 15[2(8) + (15 − 1)8]/2

= 15[16 + 112]/2

= 15[64] = 960

Por lo tanto, la suma de los primeros 15 múltiplos de 8 es 960.

(ii) los primeros 40 enteros positivos divisibles por (a) 3 (b) 5 (c) 6.

Solución: 

Sabemos que la suma de n términos de un AP está dada por, S _n = n[2a + (n − 1)d] / 2.

(a) Los primeros 40 enteros positivos divisibles por 3 son 3, 6, 9, 12,…… ,120.

Estos números enteros forman un AP con el primer término (a) = 3, 

Diferencia común (d) = 6 − 3 = 3 y número de términos (n) = 40.

S40 = 40[2(3) + (40 − ₁ )3]/2

= 40(6 + 117)/2

= 20(123) = 2460

Por lo tanto, la suma de los primeros 40 múltiplos de 3 es 2460.

(b) Los primeros 40 enteros positivos divisibles por 5 son 5, 10, 15, 20,…… ,200.

Estos números enteros forman un AP con el primer término (a) = 5, 

Diferencia común (d) = 10 − 5 = 5 y número de términos (n) = 40.

S40 = 40[2(5) + (40 − ₁ )5]/2

= 40(10 + 195)/2

= 20(205) = 4100

Por lo tanto, la suma de los primeros 40 múltiplos de 5 es 4100.

(c) Los primeros 40 enteros positivos divisibles por 6 son 6, 12, 18, 24,…… ,240.

Estos números enteros forman un AP con el primer término (a) = 6, 

Diferencia común (d) = 12 − 6 = 6 y número de términos (n) = 40.

S40 = 40[2(6) + (40 − ₁ )6]/2

= 40(12 + 234)/2

= 20(246) = 4920

Por lo tanto, la suma de los primeros 40 múltiplos de 6 es 4920.

(iii) todos los números naturales de 3 dígitos que son divisibles por 13.

Solución:

Todos los números naturales de 3 cifras que son divisibles por 13 son 104, 117,…… ,988.

Estos números forman un AP con el primer término (a) = 104 y 

Diferencia común (d) = 117 − 104 = 13.

Sabemos, el n-ésimo término de un ID de AP dado por, a _n = a + (n − 1)d.

=> 988 = 104 + (n − 1)13

=> 988 = 104 + 13n -13

=> 988 = 91 + 13n

=> 13n = 897

=> norte = 69

Además, sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

S ₆₉  = 69[2(104) + (69 − 1)13]/2

= 69[1092]/2

= 69(546) = 37674

Por lo tanto, la suma de todos los números naturales de 3 dígitos que son divisibles por 13 es 37674.

(iv) todos los números naturales de 3 dígitos que son múltiplos de 11.

Solución:

Todos los números naturales de 3 cifras que son divisibles por 11 son 110, 121, 132,…… ,990.

Estos números forman un AP con el primer término (a) = 110 y 

Diferencia común (d) = 121 − 110 = 11.

Sabemos, el n-ésimo término de un ID de AP dado por, a _n = a + (n − 1)d.

=> 990 = 110 + (n − 1)11

=> 990 = 110 + 11n -11

=> 990 = 99 + 11n

=> 11n = 891

=> norte = 81

Además, sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

S ₈₁ = 81[2(110) + (81 − 1)11]/2

= 81[1100]/2

= 81(550) = 44550

Por lo tanto, la suma de todos los números naturales de 3 dígitos que son divisibles por 13 es 44550.

(v) todos los números naturales de 2 dígitos divisibles por 4.

Solución:

Todos los números naturales de 2 cifras divisibles por 4 son 12, 16, 20,…… ,96.

Estos números forman un AP con el primer término (a) = 4 

y diferencia común (d) = 16 − 12 = 4.

Sabemos que el enésimo término de un PA está dado por, a _n = a + (n − 1)d.

=> 96 = 12 + (n − 1)4

=> 4(n − 1) = 84

=> norte − 1 = 21

=> norte = 22

Además, sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

S ₂₂ = 22[2(12) + (22 − 1)4]/2

= 22[24 + 84]/2

= 22[54] = 1188

Por lo tanto, la suma de todos los números naturales de 2 dígitos divisibles por 4 es 1188.

Pregunta 13. Encuentra la suma:

(yo) 2 + 4 + 6 + . . . + 200 

Solución:

La serie dada es un AP con el primer término (a) = 2, 

Diferencia común(d) = 4 − 2 = 2 y enésimo término(a _n ) = 200.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 200 = 2 + (n − 1)2

=> 200 = 2 + 2n − 2

=> n = 200/2 

=> n = 100

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S100 = 100[2 + 200]/ ₂

= 100[101] = 10100

Por tanto, la suma de los términos de la serie dada es 10100.

(ii) 3 + 11 + 19 + . . . + 803 

Solución:

La serie dada es un AP con el primer término (a) = 3, 

Diferencia común(d) = 11 − 3 = 8 y enésimo término(a _n ) = 803.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 803 = 3 + (n − 1)8

=> 803 = 3 + 8n − 8

=> n = 808/8 

=> n = 101

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S101 = 101[3 ₊ 803]/2

= 101[403]

= 40703

Por tanto, la suma de los términos de la serie dada es 40703.

(iii) (-5) + (-8) + (-11) + . . . + (-230) 

Solución:

La serie dada es un AP con el primer término (a) = -5, 

Diferencia común(d) = (−8) − (−5) = −3 y término n (a _n ) = −230.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> −230 = −5 + (n − 1)(−3)

=> −230 = −5 − 3n + 3

=> n = 228/3

=> norte = 76

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₇₆ = 76 [−5 + (−230)]/2

= 38 × (−235) = −8930

Por tanto, la suma de los términos de la serie dada es –8930.

(iv) 1 + 3 + 5 + 7 + . . . + 199

Solución:

La serie dada es un AP con el primer término (a) = 1,

Diferencia común(d) = 3 − 1 = 2 y enésimo término(a _n ) = 199.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 199 = 1 + (n − 1)(2)

=> 199 = 1 + 2n − 2

=> n = 200/2 

=> n = 100

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S100 = 100[1 + 199]/ ₂

= 50(200) = 10000

Por lo tanto, la suma de los términos de la serie dada es 10000.

(v) 7 + 10 ¹ / ₂ + 14 + . . . + 84

Solución:

La serie dada es un AP con el primer término (a) = 7, 

Diferencia común(d) = 10 ¹ / ₂ − 7 = (21 − 14)/2 = 7/2 y término n (a _n ) = 84.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 84 = 7 + (n − 1)(7/2)

=> 168 = 14 + 7n − 7

=> n = 161/7 

=> norte = 23

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₂₃ = 23[7 + 84]/2

= 23(91)/2

= 2093/2 = 1046,5

Por lo tanto, la suma de los términos de la serie dada es 1046.5

(vi) 34 + 32 + 30 + . . . + 10 

Solución:

La serie dada es un AP con el primer término (a) = 34, 

Diferencia común(d) = 32 − 34 = −2 y término n (a _n ) = 10.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 10 = 34 + (n − 1)(−2)

=> 10 = 34 − 2n + 2

=> n = (36 −10)/2 

=> norte = 13

Además, sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₁₃ = 13[34 + 10]/2

= 13(22)

= 286

Por tanto, la suma de los términos de la serie dada es 286.

(vi) 25 + 28 + 31 + . . . + 100   

Solución:

La serie dada es un AP con el primer término (a) = 25, 

Diferencia común(d) = 28 − 25 = 3 y enésimo término(a _n ) = 100.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 100 = 25 + (n − 1)(3)

=> 100 = 25 + 3n − 3

=> n = 88/3 

=> norte = 26

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₂₆ = 26[25 + 100]/2

= 13(125)

= 1625

Por tanto, la suma de los términos de la serie dada es 1625.

(viii) 18 + 15 ¹ / ₂ + 13 + . . . + (–49 ¹ / ₂ )

Solución:

La serie dada es un AP con el primer término (a) = 18, 

Diferencia común(d) =   − 18 = (31 − 36)/2 = −5/2 y término n (a _n ) = 

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=>   = 18+(n − 1)(−5/2)

=> –135/2 = (n − 1)(−5/2)

=> norte − 1 = 135/5

=> norte = 28

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₂₈ = 28[18 + (−49 ¹ / ₂ )]/2

= 14[−63/2]

= −441

Por tanto, la suma de los términos de la serie dada es − 441.

Pregunta 14. El primer y último término de un AP son 17 y 350 respectivamente. Si la diferencia común es 9, ¿cuántos términos hay y cuál es su suma?

Solución:

Dado que AP tiene el primer término (a) = 17, 

Diferencia común(d) = 9 y último término(a _n ) = 350.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d.

=> 350 = 17 + (n − 1) 9

=> 350 = 17 + 9n − 9

=> 9n = 342

=> norte = 38

También sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

S ₃₈ = 38(17 + 350)/2

= 19(367) = 6973

Por lo tanto, el número de términos del AP dado es 38 y la suma es 6973.

Pregunta 15. El tercer término de un AP es 7 y el séptimo término excede tres veces al tercer término en 2. Encuentra el primer término, la diferencia común y la suma de los primeros 20 términos.

Solución:

Dado que AP tiene un tercer término (a ₃ ) = 7 y un séptimo término (a ₇ ) = 3a ₃ + 2 = 3(7) + 2 = 23.

Sabemos que el término n de un PA viene dado por, a _n = a + (n − 1)d. Entonces, obtenemos,

a + 2d = 7 ….. (1)

a + 6d = 23 ….. (2)

Restando (1) de (2), obtenemos,

=> (a + 6d) − (a + 2d) = 23 − 7

=> 4d = 16

=> re = 4

Al poner d = 4 en (1), obtenemos,

=> un + 2(4) = 7

=> un = 7 − 8

=> un = −1

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

Aquí a = −1, d = −4, n = 20. Así que la suma es,

S ₂₀ = 20[2(−1) + (20 − 1)(4)]/2

= 20[-2 + 76]/2

= 20[39] = 740

Por lo tanto, la suma de los primeros 20 términos para el AP dado es 740.

Pregunta 16. El primer término de un AP es 2 y el último término es 50. La suma de todos estos términos es 442. Encuentra la diferencia común.

Solución:

Dado que AP tiene el primer término (a) = 2, el último término (a _n ) = 50 y la suma (S _n ) = 442.

Sabemos que la suma de n términos de un AP viene dada por S _n = n[a + a _n ]/2.

=> 442 = n[2 + 50]/2

=> 26n = 442

=> n = 17

Además, sabemos que el término n de un AP está dado por, a _n = a + (n − 1)d. Entonces, obtenemos,

=> 50 = 2 + (17 − 1)d

=> 16d = 48

=> re = 3

Por lo tanto, la diferencia común de AP es 3.

Pregunta 17. Si el término 12 de un AP es -13 y la suma de los primeros cuatro términos es 24, ¿cuál es la suma de los primeros 10 términos?

Solución:

Se nos da,

12º término del AP, (a ₁₂ ) = a + 11d = −13 …. (1)

Suma de los cuatro primeros términos = S ₄  = 4[2a + (4 − 1)d]/2 = 24  

=> 24 = 4[2a + 3d]/2

=> 2a + 3d = 12 ….. (2)

Al multiplicar eq(1) por 2 y restarle eq(2) obtenemos,

=> (2a+3d) − 2(a+11d) = 12 − 2(−13)

=> 2a + 3d − 2a − 22d = 38

=> −19d = 38

=> re = −2

Al poner el valor de d en la ecuación (1), obtenemos,

=> un + 11(−2) = −13

=> un = −13 + 22

=> un = 9

Ahora, la suma de los primeros 10 términos está dada por,

S ₁₀ = 10[2(9) + (10 − 1)(−2)]/2

= 10(18 – 18)/2 = 0

Por lo tanto, la suma de los primeros 10 términos del AP dado es 0.

Pregunta 18. Encuentra la suma de n términos de la serie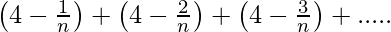 

Solución:

Dado que AP tiene el primer término (a) =  

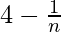
Diferencia común(d) = 

=  

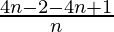
= -1/n 

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2

= 

= 

= 

= 

Por tanto, la suma de n términos del AP dado es 

Pregunta 19. En un AP, si el primer término es 22, la diferencia común es –4 y la suma de n términos es 64, encuentra n.

Solución:

Dado que AP tiene el primer término (a) = 22, la diferencia común (d) = −4 y la suma (S _n ) = 64.

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

=> 64 = n[2(22) + (n − 1)(−4)]/2

=> 64 = n[44 − 4n + 4]/2

=> 48n − 4n ² =128 

=> 4n ² − 48n + 128 = 0

=> norte ² − 12n + 32 = 0

=> norte ² − 8n − 4n + 32 = 0

=> n(n – 8) – 4(n – 8) = 0

=> (n − 8)(n − 4) = 0

=> n = 8 o n = 4

Por lo tanto, el número de términos es 4 u 8.

Pregunta 20. En un AP, si los términos 5 y 12 son 30 y 65 respectivamente, ¿cuál es la suma de los primeros 20 términos?  

Solución:

Dado que AP tiene,

Quinto término, a ₅ = a + 4d = 30 …..(1)

Duodécimo término, a ₁₂ = a + 11d = 65 ….(2)

Al restar la ecuación (1) de (2), obtenemos,

=> (a + 11d) − (a + 4d) = 65 − 30

=> 7d = 35

=> re = 5

Al poner d = 5 en la ecuación (1), obtenemos,

=> a + 4(5) = 30

=> un = 30 − 20

=> un = 10

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

Aquí a = 10, d = 5 y n = 20. Entonces obtenemos,

S ₂₀ = 20[2(10) + (20 − 1)(5)]/2

= 20[20 + 95]/2

= 10[115] = 1150

Por lo tanto, la suma de los primeros 20 términos para el AP dado es 1150.

Pregunta 21. Encuentra la suma de los primeros 51 términos de un AP cuyo segundo y tercer términos son 14 y 18 respectivamente.

Solución:

Dado que AP tiene,

Segundo término, a ₂ = a + d = 14 …..(1)

Tercer término, a ₃ = a + 2d = 18

Por lo tanto, diferencia común (d) = a ₃ − a ₂ = 18 − 14 = 4.

Al poner d = 4 en (1), obtenemos,

=> un + 4 = 14

=> un = 10

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

Aquí a = 10, d = 4 y n = 51. Entonces obtenemos,

S ₅₁ = 51[2(10) + (51 − 1)(4)]/2

= 51[20 + 200]/2

= 51[110] = 5610

Por lo tanto, la suma de los primeros 51 términos para el AP dado es 5610.

Pregunta 22. Si la suma de 7 términos de un AP es 49 y la de 17 términos es 289, encuentra la suma de n términos.

Solución:

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d]/2. 

Entonces obtenemos, S ₇ = 49

=> 7[2a + (7 − 1)d]/2 = 49

=> 7[a + 3d] = 49

=> a + 3d = 7 ….. (1)

Y también, S ₁₇ = 289

=> 17[2a + (17 − 1)d]/2 = 289

=> 17[a + 8d] = 289

=> a + 8d = 17 ….. (2)

Al restar la ecuación (1) de (2), obtenemos,

=> un + 8d − (un + 3d) = 17 − 7

=> 5d = 10

=> re = 2

Al poner d = 2 en (1), obtenemos,

=> un + 3(2) = 7

=> un = 1

Aquí a = 1, d = 2, por lo que la suma de n términos sería,

S _norte = norte[2(1) + (norte – 1)(2)]/2

= n[2 + 2n − 2]/2

= norte[n] = norte ²

Por tanto, la suma de n términos del AP dado es n ² .

Pregunta 23. El primer término de un AP es 5, el último término es 45 y la suma es 400. Encuentra el número de términos y la diferencia común.

Solución:

Dado que AP tiene el primer término (a) = 5, el último término (a _n ) = 45 y la suma (S _n ) = 400.

Sabemos que la suma de n términos de un AP viene dada por, S _n = n[a + a _n ]/2

=> 400 = n[5 + 45]/2

=> 50n = 800

=> norte = 16

Además, conocemos el término enésimo de un PA dado por, a _n = a + (n − 1)d.

=> 45 = 5 + (16 − 1)d

=> 15d = 40

=> re = 8/3

Por tanto, el número de términos de AP dado es 16 y la diferencia común es 8/3.

Pregunta 24. En un AP el primer término es 8, el n-ésimo término es 33 y la suma de los primeros n términos es 123. Encuentra n y la d, la diferencia común.  

Solución:

Dado que AP tiene el primer término (a) = 8, el enésimo término (a _n ) = 33 y la suma (S _n ) = 123.

Sabemos que la suma de n términos de un AP viene dada por, S _n = n[a + a _n ]/2

=> 123 = n[8 + 33]/2

=> 41n = 246

=> norte = 6

Además, conocemos el término enésimo de un PA dado por, a _n = a + (n − 1)d.

=> 33 = 8 + (6 − 1)d

=> 5d = 25

=> re = 5

Por lo tanto, el número de términos de AP dado es 6 y la diferencia común es 5.