Cálculo de vectores propios y aproximaciones de rango bajo

Prerrequisitos: valores propios y vectores propios

Antes de profundizar en las matemáticas detrás de los cálculos relacionados con los vectores propios, discutamos brevemente qué son realmente un valor propio y un vector propio.

Valor propio y vectores propios:

La palabra ‘eigen’ significa ‘ características ‘. En términos generales, los valores propios y los vectores propios dan las características de una array o un vector.

Vector propio : es un vector representado por una array X tal que cuando X se multiplica con cualquier array A, la dirección de la array resultante sigue siendo la misma que la del vector X. Observe la Fig. 1 cuidadosamente para ver una representación gráfica de un vector propio.

Fig. 1: Representación del vector propio

En la figura 1, observamos las siguientes transformaciones escalares:

$\vec{v_1'} = 1.5 (\vec{v_1}) \\ \vec{v_2'} = 0.5 (\vec{v_2})$

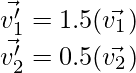
Después de aplicar estas transformaciones, los vectores v ₁ ‘ y v ₂ ‘ están en la misma dirección que v ₁ y v ₂ . Entonces, según nuestra definición, estos se consideran vectores propios. Pero el vector resultante v ₃ ‘ no está en la misma dirección que v ₃ . Por lo tanto, no puede ser considerado como un vector propio.

Valores propios: nos informa sobre la medida en que el vector propio se ha estirado o disminuido.
En el caso anterior, los valores propios serán 1,5 y 0,5 .

Cálculo de vectores propios

Podemos calcular los valores propios de cualquier array usando la ecuación característica de la array (como se discutió en el artículo de requisitos previos) que es:

$|A - \lambda I|= 0$

Las raíces de la ecuación anterior ( es decir, los valores de λ ) nos dan los valores propios.

Usando los valores de λ obtenidos, podemos encontrar los vectores propios correspondientes usando la ecuación dada a continuación.

$At\ \lambda=i\\ [A-iI ]X_i = 0$

Problema de ejemplo

Considere el siguiente ejemplo para una mejor comprensión. Sea una array X de 3×3 definida como:

$A = \begin{bmatrix} 1 & 0 & -1\\1 & 2 & 1\\2 & 2 & 3 \end{bmatrix}$

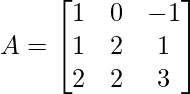
Encuentre los valores propios y los vectores propios correspondientes a la array A.

Solución

1. Encontrar los valores propios.

$\\ det(A-\lambda I) = det(\begin{bmatrix} 1-\lambda & 0 & -1\\1 & 2-\lambda & 1\\2 & 2 & 3-\lambda \end{bmatrix}) = 0 \\ \implies (\lambda^3 - 6\lambda^2 +11\lambda -6) = 0 \\ \implies (\lambda - 1)( \lambda - 2)(\lambda -3) = 0 \\ \implies \lambda = 1,2,3$

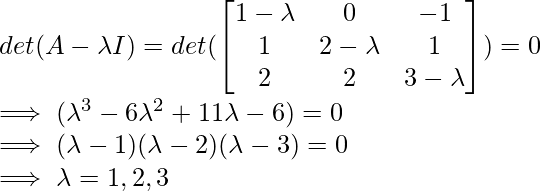
Así, los valores propios obtenidos son 1, 2 y 3.

2. Hallar los vectores propios.

Usando la fórmula anterior, calcularemos un vector propio x _i correspondiente para cada valor de λ _i .

$At\ \lambda = 1 \\ [A - (1)I]X_1 = 0 \\ \implies \begin{bmatrix} 1-1 & 0 & -1\\1 & 2-1 & 1\\2 & 2 & 3-1 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ \implies \begin{bmatrix} 0 & 0 & -1\\1 & 1 & 1\\2 & 2 & 2 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ On\ solving,\ we\ get\ the\ following\ equations: \\ x_3 = 0 (x_1) \\ x_1 + x_2 = 0 \implies x_2 = -x_1 \\ \therefore X_1 = \begin{bmatrix} x_1\\-x_1\\ 0(x_1) \end{bmatrix} \\ \implies X_1 = \begin{bmatrix} 1\\-1\\0 \end{bmatrix}$
$Similarly, \\ for\ \lambda = 2 \\ X_2 = \begin{bmatrix} -2\\1\\2 \end{bmatrix} \\ and \\ for\ \lambda = 3 \\ X_3 = \begin{bmatrix} 1\\-1\\-2 \end{bmatrix}$

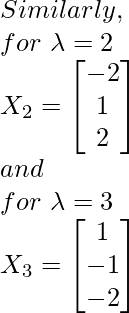
Así, obtenemos los vectores propios X ₁ , X ₂ , X ₃ correspondientes a cada valor de λ.

Rango de una array:

El rango de una array (mxn) está determinado por el número de filas linealmente independientes presentes en la array. Considere el ejemplo dado a continuación para una mejor comprensión.

$A = \begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{bmatrix}$

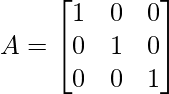
Las 3 filas de la array A son linealmente independientes. Por lo tanto, Rango ( A ) = 3 .

$B = \begin{bmatrix} 2 & 1 & 3\\3 & 2 & 0\\5 & 3 & 3 \end{bmatrix} \\$

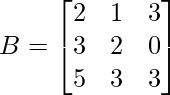
Rango ( B ) = 2. Esto se debe a que la Fila 3 depende de R ₁ y R ₂ . [R ₃ <- R ₁ + R ₂ ]

Algunas propiedades importantes:

Para cualquier array A de forma mxn, se aplican las siguientes propiedades de rango:

Rango (A) = Rango (A ^T )
Rango (BAC) = Rango (A) siempre que B y C sean arrays invertibles.
Rango (AB) ≤ min{ Rango (A) + Rango (B) }

Antes de entrar en la aproximación de rango bajo, es importante comprender lo siguiente:

Factorización de arrays

Se dice que cualquier array A de forma mxn de rango (A) = r está factorizada cuando toma la forma:

$A = BC^T$

where, the shapes of the matrices are:
 
mat(A) -> m x n
mat(B) -> m x r 
mat(C) -> n x r

Bajo rango

Decimos que la array A tiene un rango bajo si r << min {m,n} .

Aproximación de rango bajo (LRA)

Con base en los dos métodos discutidos anteriormente, definimos LRA como:

Para una array A de forma mxn y rango (A) << min {m, n}, la aproximación de rango bajo de A es encontrar otra array B tal que rango (B) ≤ rango (A). Intuitivamente, tendemos a ver cuán linealmente similar es la array B a la array de entrada A. Matemáticamente, LRA es un problema de minimización, en el que medimos el ajuste entre una array dada (los datos) y una array aproximada (la variable de optimización).

Motivación para LRA

Supongamos 3 arrays X, Y, Z de dimensiones (50 x 40), (50 x 10), (40 x 10) respectivamente donde rank(X) = 10. Por lo tanto, según la factorización matricial, las tres arrays son de la forma A = BC ^T . Observamos que:

A_{mxn = BmxrC^Trxn}

No of elements/pixels in mat(A) = (50 x 40) = 2000
while
No of elements/pixels in mat(BC^T) = (50 x 10) + (10 x 40) = 900.

Por lo tanto, al usar una aproximación de rango bajo, podemos reducir la cantidad de píxeles de los datos de entrada en una cantidad significativa. (1100 píxeles menos que la imagen de entrada en el caso anterior)

Aplicación de LRA

Este método se usa comúnmente en tareas de procesamiento de imágenes donde la imagen de entrada (datos) es muy grande y debe comprimirse antes de cualquier tarea de procesamiento. Observe las dos imágenes de la misma persona que se dan a continuación.

Después de la imagen LRA frente a la imagen de entrada

Después de aplicar LRA, podemos obtener una imagen muy similar a la imagen original al descartar algunos píxeles sin importancia, por lo que también se reduce el tamaño de la imagen. Después de hacer esto, se vuelve mucho más fácil manejar conjuntos de datos tan grandes y realizar una variedad de tareas de preprocesamiento en ellos.

Publicación traducida automáticamente

Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA