Pregunta 1. Encuentra los intervalos en los que las siguientes funciones son crecientes o decrecientes.
(yo) f(x) = 10 – 6x – 2x 2
Solución:
Se nos da,
f(x) = 10 – 6x – 2x 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 0 – 6 – 4x
f'(x) = – 6 – 4x
Para que f(x) sea creciente, debemos tener,
=> f'(x) > 0
=> – 6 – 4x > 0
=> – 4x > 6
=> x < –6/4
=> x < –3/2
=> x ∈ (–∞, –3/2)
Para que f(x) sea decreciente, debemos tener,
=> f'(x) < 0
=> – 6 – 4x < 0
=> – 4x <6
=> x > –6/4
=> x > –3/2
=> x ∈ ( –3/2, ∞)
Así, f(x) es creciente en el intervalo x ∈ (–∞, –3/2) y decreciente en el intervalo x ∈ (–3/2, ∞).
(ii) f(x) = x2 + 2x – 5
Solución:
Se nos da,
f(x) = x2 + 2x – 5
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 2x + 2 – 0
f'(x) = 2x + 2
Para que f(x) sea creciente, debemos tener,
=> f'(x) > 0
=> 2x + 2 > 0
=> 2x > –2
=> x > –2/2
=> x > –1
=> x ∈ (–1, ∞)
Para que f(x) sea decreciente, debemos tener,
=> f'(x) < 0
=> 2x + 2 < 0
=> 2x < –2
=> x < –2/2
=> x < –1
=> x ∈ (–∞, –1)
Así, f(x) es creciente en el intervalo x ∈ (–1, ∞) y decreciente en el intervalo x ∈ (–∞, –1).
(iii) f(x) = 6 – 9x – x 2
Solución:
Se nos da,
f(x) = 6 – 9x – x 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 0 – 9 – 2x
f'(x) = – 9 – 2x
Para que f(x) sea creciente, debemos tener,
=> f'(x) > 0
=> –9 – 2x > 0
=> –2x > 9
=> x > –9/2
=> x ∈ (–9/2, ∞)
Para que f(x) sea decreciente, debemos tener,
=> f'(x) < 0
=> –9 – 2x < 0
=> –2x < 9
=> x < –9/2
=> x ∈ (–∞, –9/2)
Así, f(x) es creciente en el intervalo x ∈ (–9/2, ∞) y decreciente en el intervalo x ∈ (–∞, –9/2).
(iv) f(x) = 2x 3 – 12x 2 + 18x + 15
Solución:
Se nos da,
f(x) = 2x 3 – 12x 2 + 18x + 15
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 – 24x + 18 + 0
f'(x) = 6x 2 – 24x + 18
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 2 – 24x + 18 = 0
=> 6 (x 2 – 4x + 3) = 0
=> x2 – 4x + 3 = 0
=> x2 – 3x – x + 3 = 0
=> x (x – 3) – 1 (x – 3) = 0
=> (x-1) (x-3) = 0
=> x = 1, 3
Claramente, f'(x) > 0 si x < 1 y x > 3.
Además, f'(x) < 0, si 1 < x < 3.
Así, f(x) es creciente en el intervalo x ∈ (–∞, 1)∪ (3, ∞) y decreciente en el intervalo x ∈ (1, 3).
(v) f(x) = 5 + 36x + 3x 2 – 2x 3
Solución:
Se nos da,
f(x) = 5 + 36x + 3x 2 – 2x 3
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 0 + 36 + 6x – 6x 2
f'(x) = 36 + 6x – 6x 2
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 36 + 6x – 6x 2 = 0
=> 6 (– x 2 + x + 6) = 0
=> 6 (–x 2 + 3x – 2x + 6) = 0
=> –x 2 + 3x – 2x + 6 = 0
=> x 2 – 3x + 2x – 6 = 0
=> (x – 3) (x + 2) = 0
=> x = 3, – 2
Claramente, f'(x) > 0 si –2 < x < 3.
También f'(x) < 0 si x < –2 y x > 3.
Así, f(x) crece en x ∈ (–2, 3) y f(x) decrece en el intervalo x ∈ (–∞, –2) ∪ (3, ∞).
(vi) f(x) = 8 + 36x + 3x 2 – 2x 3
Solución:
Se nos da,
f(x) = 8 + 36x + 3x 2 – 2x 3
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 0 + 36 + 6x – 6x 2
f'(x) = 36 + 6x – 6x 2
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 36 + 6x – 6x 2 = 0
=> 6 (– x 2 + x + 6) = 0
=> 6 (–x 2 + 3x – 2x + 6) = 0
=> –x 2 + 3x – 2x + 6 = 0
=> x 2 – 3x + 2x – 6 = 0
=> (x – 3) (x + 2) = 0
=> x = 3, –2
Claramente, f'(x) > 0 si –2 < x < 3.
También f'(x) < 0 si x < –2 y x > 3.
Así, f(x) crece en x ∈ (–2, 3) y f(x) decrece en el intervalo x ∈ (–∞, –2) ∪ (3, ∞).
(vii) f(x) = 5x 3 – 15x 2 – 120x + 3
Solución:
Se nos da,
f(x) = 5x 3 – 15x 2 – 120x + 3
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 15x 2 – 30x – 120 + 0
f'(x) = 15x 2 – 30x – 120
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 15x 2 – 30x – 120 = 0
=> 15(x 2 – 2x – 8) = 0
=> 15(x 2 – 4x + 2x – 8) = 0
=> x 2 – 4x + 2x – 8 = 0
=> (x – 4) (x + 2) = 0
=> x = 4, –2
Claramente, f'(x) > 0 si x < –2 y x > 4.
También f'(x) < 0 si –2 < x < 4.
Así, f(x) es creciente en x ∈ (–∞,–2) ∪ (4, ∞) y f(x) es decreciente en el intervalo x ∈ (–2, 4).
(viii) f(x) = x 3 – 6x 2 – 36x + 2
Solución:
Se nos da,
f(x) = x 3 – 6x 2 – 36x + 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – 12x – 36 + 0
f'(x) = 3x 2 – 12x – 36
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 3x 2 – 12x – 36 = 0
=> 3(x 2 – 4x – 12) = 0
=> 3(x 2 – 6x + 2x – 12) = 0
=> x 2 – 6x + 2x – 12 = 0
=> (x – 6) (x + 2) = 0
=> x = 6, –2
Claramente, f'(x) > 0 si x < –2 y x > 6.
También f'(x) < 0 si –2< x < 6
Así, f(x) es creciente en x ∈ (–∞,–2) ∪ (6, ∞) y f(x) es decreciente en el intervalo x ∈ (–2, 6).
(ix) f(x) = 2x 3 – 15x 2 + 36x + 1
Solución:
Se nos da,
f(x) = 2x 3 – 15x 2 + 36x + 1
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 – 30x + 36 + 0
f'(x) = 6x 2 – 30x + 36
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 2 – 30x + 36 = 0
=> 6 (x 2 – 5x + 6) = 0
=> 6(x 2 – 3x – 2x + 6) = 0
=> x 2 – 3x – 2x + 6 = 0
=> (x-3) (x-2) = 0
=> x = 3, 2
Claramente, f'(x) > 0 si x < 2 y x > 3.
También f'(x) < 0 si 2 < x < 3.
Así, f(x) es creciente en x ∈ (–∞, 2) ∪ (3, ∞) y f(x) es decreciente en el intervalo x ∈ (2, 3).
(x) f(x) = 2x 3 + 9x 2 + 12x + 1
Solución:
Se nos da,
f(x) = 2x 3 + 9x 2 + 12x + 1
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 + 18x + 12 + 0
f'(x) = 6x 2 + 18x + 12
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6×2 + 18x + 12 = 0
=> 6 (x2 + 3x + 2) = 0
=> 6(x2 + 2x + x + 2) = 0
=> x2 + 2x + x + 2 = 0
=> (x + 2) (x + 1) = 0
=> x = –1, –2
Claramente, f'(x) > 0 si –2 < x < –1.
También f'(x) < 0 si x < –1 y x > –2.
Así, f(x) crece en x ∈ (–2,–1) y f(x) decrece en el intervalo x ∈ (–∞, –2) ∪ (–2, ∞).
(xi) f(x) = 2x 3 – 9x 2 + 12x – 5
Solución:
Se nos da,
f(x) = 2x 3 – 9x 2 + 12x – 5
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 – 18x + 12 – 0
f'(x) = 6x 2 – 18x + 12
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 2 – 18x + 12 = 0
=> 6 (x 2 – 3x + 2) = 0
=> 6(x 2 – 2x – x + 2) = 0
=> x2 – 2x – x + 2 = 0
=> (x-2) (x-1) = 0
=> x = 1, 2
Claramente, f'(x) > 0 si x < 1 y x > 2.
También f'(x) < 0 si 1 < x < 2.
Así, f(x) es creciente en x ∈ (–∞, 1) ∪ (2, ∞) y f(x) es decreciente en el intervalo x ∈ (1, 2).
(xii) f(x) = 6 + 12x + 3x 2 – 2x 3
Solución:
Se nos da,
f(x) = 6 + 12x + 3x 2 – 2x 3
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 0 + 12 + 6x – 6x 2
f'(x) = 12 + 6x – 6x 2
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 12 + 6x – 6x 2 = 0
=> 6 (–x 2 + x + 2) = 0
=> x2 – x – 2 = 0
=> x2 – 2x + x – 2 = 0
=> (x – 2) (x + 1) = 0
=> x = 2, –1
Claramente, f'(x) > 0 si –1 < x < 2.
También f'(x) < 0 si x < –1 y x > 2.
Así, f(x) crece en x ∈ (–1, 2) y f(x) decrece en el intervalo x ∈ (–∞, –1) ∪ (2, ∞).
(xiii) f(x) = 2x 3 – 24x + 107
Solución:
Se nos da,
f(x) = 2x 3 – 24x + 107
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 – 24 + 0
f'(x) = 6x 2 – 24
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 2 – 24 = 0
=> 6×2 = 24
=> x2 = 4
=> x = 2, –2
Claramente, f'(x) > 0 si x < –2 y x > 2.
También f'(x) < 0 si –2 < x < 2.
Así, f(x) crece en x ∈ (–∞, –2) ∪ (2, ∞), y f(x) decrece en el intervalo x ∈ (–2, 2).
(xiv) f(x) = –2x 3 – 9x 2 – 12x + 1
Solución:
Se nos da,
f(x) = –2x 3 – 9x 2 – 12x + 1
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = –6x 2 – 18x – 12 + 0
f'(x) = –6x 2 – 18x – 12
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> –6x 2 – 18x – 12 = 0
=> 6 (–x 2 – 3x – 2) = 0
=> x2 + 3x + 2 = 0
=> x2 + 2x + x + 2 = 0
=> (x + 2) (x + 1) = 0
=> x = –2, –1
Claramente, f'(x) > 0 si x < –1 yx > –2.
Además, f'(x) < 0 si –2 < x < –1.
Así, f(x) crece en x ∈ (–2, –1) y f(x) decrece en el intervalo x ∈ (–∞, –2) ∪ (–1, ∞).
(xv) f(x) = (x – 1) (x – 2) 2
Solución:
Se nos da,
f(x) = (x – 1) (x – 2) 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = (x – 2) 2 + 2 (x – 1) (x – 2)
f'(x) = (x – 2) (x – 2 + 2x – 2)
f'(x) = (x – 2) (3x – 4)
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> (x – 2) (3x – 4) = 0
=> x = 2, 4/3
Claramente, f'(x) > 0 si x < 4/3 y x > 2.
Además, f'(x) < 0 si 4/3 < x < 2.
Así, f(x) es creciente en x ∈ (–∞, 4/3) ∪ (2, ∞) y f(x) es decreciente en el intervalo x ∈ (4/3, 2).
(xvi) f(x) = x 3 – 12x 2 + 36x + 17
Solución:
Se nos da,
f(x) = x3 – 12×2 + 36x + 17
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – 24x + 36 + 0
f'(x) = 3x 2 – 24x + 36
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 3x 2 – 24x + 36 = 0
=> 3 (x 2 – 8x + 12) = 0
=> x2 – 8x + 12 = 0
=> x 2 – 6x – 2x + 12 = 0
=> (x-6) (x-2) = 0
=> x = 6, 2
Claramente, f'(x) > 0 si x < 2 y x > 6.
Además, f'(x) < 0 si 2 < x < 6.
Así, f(x) es creciente en x ∈ (–∞, 2) ∪ (6, ∞) y f(x) es decreciente en el intervalo x ∈ (2, 6).
(xvii) f(x) = 2x 3 – 24x + 7
Solución:
Se nos da,
f(x) = 2x 3 – 24x + 7
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 2 – 24 + 0
f'(x) = 6x 2 – 24
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 2 – 24 = 0
=> 6×2 = 24
=> x2 = 4
=> x = 2, –2
Claramente, f'(x) > 0 si x < –2 y x > 2.
También f'(x) < 0 si –2 < x < 2.
Así, f(x) crece en x ∈ (–∞, –2) ∪ (2, ∞), y f(x) decrece en el intervalo x ∈ (–2, 2).
(xviii) f(x) = 3x 4 /10 – 4x 3 /5 -3x 2 + 36x/5 + 11
Solución:
Se nos da,
f(x) = 3x 4 /10 – 4x 3 /5 -3x 2 + 36x/5 + 11
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 3/5 – 12x 2/5 -3(2x) + 36/5
f'(x) = 6/5[(x – 1)(x + 2)(x – 3)]
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6/5[(x – 1)(x + 2)(x – 3)] = 0
=> x = 1, –2, 3
Claramente, f'(x) > 0 si –2 < x < 1 y si x > 3
También f'(x) < 0 si 1 < x < 3.
Así, f(x) es creciente en x ∈ (3, ∞) y f(x) es decreciente en el intervalo x ∈ (1, 3).
(xix) f(x) = x 4 – 4x
Solución:
Se nos da,
f(x) = x4 – 4x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 4x 3 – 4
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 4x 3 – 4 = 0
=> 4 (x 3 – 1) = 0
=> x 3 – 1 = 0
=>x3 = 1
=> x = 1
Claramente, f'(x) > 0 si x > 1.
También f'(x) < 0 si x < 1.
Así, f(x) crece en x ∈ (1, ∞), y f(x) decrece en el intervalo x ∈ (–∞, 1).
(xx) f(x) = x 4 /4 + 2/3x 3 – 5/2x 2 – 6x + 7
Solución:
Tenemos,
f(x) = x 4 /4 + 2/3x 3 – 5/2x 2 – 6x + 7
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 4x 3 /4 + 6x 2 /3 – 10x/2 – 6 + 0
f'(x) = x 3 + 2x 2 – 5x – 6
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> x3 + 2×2 – 5x – 6 = 0
=> (x + 1) (x + 3) (x – 2) = 0
=> x = –1, –3, 2
Claramente f'(x) > 0 si –3 < x < –1 y x > 2.
También f'(x) < 0 si x < –3 y –1 < x < 2.
Así, f(x) crece en x ∈ (–3, –1) ∪ (2, ∞) y f(x) decrece en el intervalo x ∈ (–∞, –3) ∪ (–1, 2).
(xxi) f(x) = x 4 – 4x 3 + 4x 2 + 15
Solución:
Tenemos,
f(x) = x 4 – 4x 3 + 4x 2 + 15
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 4x 3 – 12x 2 + 8x + 0
f'(x) = 4x 3 – 12x 2 + 8x
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 4x 3 – 12x 2 + 8x = 0
=> 4x (x2 – 3x + 2) = 0
=> 4x (x – 2) (x – 1) = 0
=> x = 0, 1, 2
Claramente f'(x) > 0 si 0 < x < 1 y x > 2.
También f'(x) < 0 si x < 0 y 1 < x < 2.
Así, f(x) es creciente en x ∈ (0, 1) ∪ (2, ∞) y f(x) es decreciente en el intervalo x ∈ (–∞, 0) ∪ (1, 2).
(xxii) f(x) = 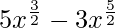 , x > 0
, x > 0
Solución:
Tenemos,
f(x) =
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=>
= 0
=>
= 0
=> x 1/2 (1 – x) = 0
=> x = 0, 1
Claramente f'(x) > 0 si 0 < x < 1.
También f'(x) < 0 si x > 0.
Así, f(x) es creciente en x ∈ (0, 1) y f(x) es decreciente en el intervalo x ∈ (1, ∞).
(xxiii) f(x) = x 8 + 6x 2
Solución:
Tenemos,
f(x) = x 8 + 6x 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 8x 7 + 12x
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 8x 7 + 12x = 0
=> 4x (2x 6 + 3) = 0
=> x = 0
Claramente f'(x) > 0 si x > 0.
También f'(x) < 0 si x < 0.
Así, f(x) crece en x ∈ (0, ∞) y f(x) decrece en el intervalo x ∈ (–∞, 0).
(xxiv) f(x) = x 3 – 6x 2 + 9x + 15
Solución:
Se nos da,
f(x) = x3 – 6×2 + 9x + 15
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – 12x + 9 + 0
f'(x) = 3x 2 – 12x + 9
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 3x 2 – 12x + 9 = 0
=> 3 (x 2 – 4x + 3) = 0
=> x2 – 4x + 3 = 0
=> x2 – 3x – x + 3 = 0
=> (x-3) (x-1) = 0
=> x = 3, 1
Claramente f'(x) > 0 si x < 1 y x > 3.
También f'(x) < 0 si 1 < x < 3.
Así, f(x) es creciente en x ∈ (–∞, 1) ∪ (3, ∞) y f(x) es decreciente en el intervalo x ∈ (1, 3).
(xxv) f(x) = [x(x – 2)] 2
Solución:
Se nos da,
f(x) = [x(x – 2)] 2
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
f'(x) = 2 (x 2 – 2x) (2x – 2)
f'(x) = 4x (x – 2) (x – 1)
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 4x (x – 2) (x – 1) = 0
=> x = 0, 1, 2
Claramente f'(x) > 0 si 0 < x < 1 y x > 2.
También f'(x) < 0 si x < 0 y 1< x < 2.
Así, f(x) es creciente en x ∈ (0, 1) ∪ (2, ∞) y f(x) es decreciente en el intervalo x ∈ (–∞, 0) ∪ (1, 2).
(xxvii) f(x) = 3x 4 – 4x 3 – 12x 2 + 5
Solución:
Se nos da,
f(x) = 3x 4 – 4x 3 – 12x 2 + 5
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 12x 3 – 12x 2 – 24x
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 12x 3 – 12x 2 – 24x = 0
=> 12x (x 2 – x – 2) = 0
=> 12x (x + 1) (x – 2) = 0
=> x = 0, –1, 2
Claramente f'(x) > 0 si –1 < x < 0 y x > 2.
También f'(x) < 0 si x < –1 y 0< x < 2.
Así, f(x) crece en x ∈ (–1, 0) ∪ (2, ∞) y f(x) decrece en el intervalo x ∈ (–∞, –1) ∪ (0, 2).
(xxvii) f(x) = 3x 4 /2 – 4x 3 – 45x 2 + 51
Solución:
Tenemos,
f(x) = 3x 4 /2 – 4x 3 – 45x 2 + 51
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 6x 3 – 12x 2 – 90x
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 6x 3 – 12x 2 – 90x = 0
=> 6x (x2 – 2x – 15) = 0
=> 6x (x + 3) (x – 5) = 0
=> x = 0, –3, 5
Claramente f'(x) > 0 si –3 < x < 0 y x > 5.
También f'(x) < 0 si x < –3 y 0< x < 5.
Así, f(x) crece en x ∈ (–3, 0) ∪ (5, ∞) y f(x) decrece en el intervalo x ∈ (–∞, –3) ∪ (0, 5).
(xxvii) f(x) = 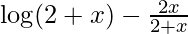
Solución:
Tenemos,
f(x) =
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
f'(x) =
f'(x) =
f'(x) =
f'(x) =
Claramente f'(x) > 0 si x > 2.
También f'(x) < 0 si x < 2
Así, f(x) es creciente en x ∈ (2, ∞) y f(x) es decreciente en el intervalo x ∈ (–∞, 2).
Pregunta 2. Determine los valores de x para los cuales la función f(x) = x 2 – 6x + 9 es creciente o decreciente. Además, encuentre las coordenadas del punto en la curva y = x 2 – 6x + 9 donde la normal es paralela a la línea y = x + 5.
Solución:
Dado f(x) = x 2 – 6x + 9
Al diferenciar ambos lados con respecto a x, obtenemos
=> f'(x) = 2x – 6
=> f'(x) = 2(x – 3)
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> 2(x-3) = 0
=> (x-3) = 0
=> x = 3
Claramente, f'(x) > 0 si x > 3.
También f'(x) < 0 si x < 3.
Así, f(x) crece en (3, ∞) y f(x) decrece en el intervalo x ∈ (–∞, 3).
La ecuación de la curva dada es f(x) = x 2 – 6x + 9.
La pendiente de esta curva está dada por,
=> m 1 = dy/dx
=> metro 1 = 2x – 6
Y la pendiente de la recta es y = x + 5
La pendiente de esta curva está dada por,
=> m 2 = dy/dx
=> metro 2 = 1
Ahora de acuerdo con la pregunta,
=> metro 1 metro 2 = –1
=> 2x – 6 = –1
=> 2x = 5
=> x = 5/2
Poniendo x = 5/2 en la curva y = x 2 – 6x + 9, obtenemos,
=> y = (5/2) 2 – 6 (5/2) + 9
=> y = 25/4 – 15 + 9
=> y = 1/4
Por lo tanto, las coordenadas requeridas son (5/2, 1/4).
Pregunta 3. Encuentra los intervalos en los que f(x) = sen x – cos x, donde 0 < x < 2π es creciente o decreciente.
Solución:
Tenemos,
f(x) = sen x – cos x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) = \frac{d}{dx}(sen x – cos x)
f'(x) = cos x + sen x
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> cos x + sen x = 0
=> 1 + tan x = 0
=> tan x = –1
=> x = 3π/4, 7π/4
Claramente f'(x) > 0 si 0 < x < 3π/4 y 7π/4 < x < 2π.
También f'(x) < 0 si 3π/4 < x < 7π/4.
Así, f(x) es creciente en x ∈ (0, 3π/4) ∪ (7π/4, 2π) y f(x) es decreciente en el intervalo x ∈ (3π/4, 7π/4).
Pregunta 4. Muestre que f(x) = e 2x es creciente en R.
Solución:
Tenemos,
=> f(x) = e 2x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 2e 2x
Para que f(x) sea creciente, debemos tener
=> f'(x) > 0
=> 2e 2x > 0
=> e 2x > 0
Ahora sabemos que el valor de e se encuentra entre 2 y 3. Por lo tanto, f(x) siempre será mayor que cero.
Por tanto, f(x) es creciente en el intervalo R.
Por lo tanto probado.
Pregunta 5. Muestre que f(x) = e 1/x , x ≠ 0 es una función decreciente para todo x ≠ 0.
Solución:
Tenemos,
=> f(x) = e 1/x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = -e x /x 2
Como x ∈ R, tenemos,
=> e x > 0
Además, obtenemos,
=> 1/x 2 > 0
Esto significa, e x /x 2 > 0
=> -e x /x 2 < 0
Así, f(x) es una función decreciente para todo x ≠ 0.
Por lo tanto probado.
Pregunta 6. Muestre que f(x) = log a x, 0 < a < 1 es una función decreciente para todo x > 0.
Solución:
Tenemos,
=> f(x) = log a x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 1/xloga
Como se nos da 0 < a < 1,
=> registrar un < 0
Y para x > 0, 1/x > 0
Por lo tanto, f'(x) es,
=> 1/xloga < 0
=> f'(x) < 0
Por tanto, f(x) es una función decreciente para todo x > 0.
Por lo tanto probado.
Pregunta 7. Muestre que f(x) = sen x crece en (0, π/2) y decrece en (π/2, π) y no crece ni decrece en (0, π).
Solución:
Tenemos,
f(x) = sen x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = cos x
Ahora para 0 < x < π/2,
=> cos x > 0
=> f'(x) > 0
Y para π/2 < x < π,
=> porque x < 0
=> f'(x) < 0
Así, f(x) es creciente en x ∈ (0, π/2) y f(x) es decreciente en el intervalo x ∈ (π/2, π).
Por tanto, f(x) no es ni creciente ni decreciente en (0, π).
Por lo tanto probado.
Pregunta 8. Muestre que f(x) = log sen x es creciente en (0, π/2) y decreciente en (π/2, π).
Solución:
Tenemos,
f(x) = log sen x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = (1/senx)cosx
f'(x) = cuna x
Ahora para 0 < x < π/2,
=> cuna x > 0
=> f'(x) > 0
Y para π/2 < x < π,
=> porque x < 0
=> f'(x) < 0
Así, f(x) es creciente en x ∈ (0, π/2) y f(x) es decreciente en el intervalo x ∈ (π/2, π).
Por lo tanto probado.
Pregunta 9. Demuestra que f(x) = x – sen x es creciente para todo x ∈ R.
Solución:
Tenemos,
f(x) = x – sen x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 1 – cos x
Ahora, nos dan x ∈ R, obtenemos
=> –1 < cos x < 1
=> –1 > cos x > 0
=> f'(x) > 0
Por tanto, f(x) es creciente en el intervalo x ∈ R.
Por lo tanto probado.
Pregunta 10. Muestre que f(x) = x 3 – 15x 2 + 75x – 50 es una función creciente para todo x ∈ R.
Solución:
Tenemos,
f(x) = x 3 – 15x 2 + 75x – 50
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – 30x + 75 – 0
f'(x) = 3x 2 – 30x + 75
f'(x) = 3(x 2 – 10x + 25)
f'(x) = 3(x – 5) 2
Ahora, como nos dan x ϵ R, obtenemos
=> (x – 5) 2 > 0
=> 3(x – 5) 2 > 0
=> f'(x) > 0
Por tanto, f(x) es creciente en el intervalo x ∈ R.
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA