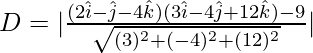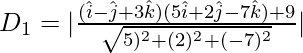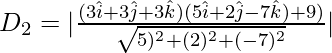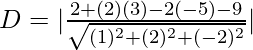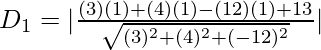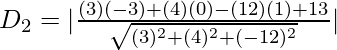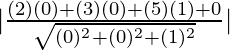Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.9

Pregunta 1. Encuentra la distancia del punto 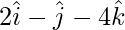$2\hat{i}-\hat{j}-4\hat{k}$ desde el plano .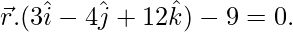 $\vec{r}.(3\hat{i}-4\hat{j}+12\hat{k})-9=0.$

Solución:

Como sabemos la distancia de un punto $\vec{a}$ a un plano $\vec{r}.\vec{n}=d$ viene dada por:

$D=|\frac{\vec{a}\vec{n}-d}{|\vec{n}|}|units$

Aquí, $a = 2\hat{i}-\hat{j}-4\hat{k}$ y $\vec{r}.(3\hat{i}-4\hat{j}+12\hat{k})-9=0$ es el avión.

Por eso, $D=|\frac{(2\hat{i}-\hat{j}-4\hat{k})(3\hat{i}-4\hat{j}+12\hat{k})-9}{\sqrt{(3)^2+(-4)^2+(12)^2}}|$

⇒ $D=|\frac{(2)(3)+(-1)(-4)+(-4)(12)-9}{\sqrt{9+16+144}}|$

= |-47/13| unidades

= 47/13 unidades

Por tanto, la distancia del punto al plano es 47/13 unidades.

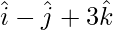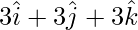Pregunta 2. Demuestra que los puntos $\hat{i}-\hat{j}+3\hat{k}$ y $3\hat{i}+3\hat{j}+3\hat{k}$ son equidistantes del plano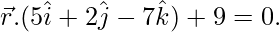 $\vec{r}.(5\hat{i}+2\hat{j}-7\hat{k})+9=0.$

Solución:

Como sabemos la distancia de un punto $\vec{a}$ a un plano $\vec{r}.\vec{n}=d$ viene dada por:

$D=|\frac{\vec{a}\vec{n}-d}{|\vec{n}|}|units$

Sea D ₁ la distancia de $\hat{i}-\hat{j}+3\hat{k}$ desde el plano $\vec{r}.(5\hat{i}+2\hat{j}-7\hat{k})+9=0.$

⇒ $D_1=|\frac{(\hat{i}-\hat{j}+3\hat{k})(5\hat{i}+2\hat{j}-7\hat{k})+9}{\sqrt{5)^2+(2)^2+(-7)^2}}|$

= $|\frac{5-2-21+9}{\sqrt{78}}|$

= 9/√78 unidades …….(1)

Ahora, sea D ₂ la distancia entre el punto $3\hat{i}+3\hat{j}+3\hat{k}$ y el plano $\vec{r}.(5\hat{i}+2\hat{j}-7\hat{k})+9=0$ .

⇒ $D_2=|\frac{(3\hat{i}+3\hat{j}+3\hat{k})(5\hat{i}+2\hat{j}-7\hat{k})+9)}{\sqrt{5)^2+(2)^2+(-7)^2}}|$

= $|\frac{15+6-21+9}{\sqrt{78}}|$

= 9/√78 unidades ……(2)

De la ecuación (1) y (2), tenemos

Los puntos dados son equidistantes del plano dado.

Pregunta 3. Encuentra la distancia del punto (2, 3, −5) desde el plano x + 2y − 2z − 9 = 0.

Solución:

Como sabemos la distancia está dada por:

$|\frac{ax_1+by_1+cz_1+d}{\sqrt{(a)^2+(b)^2+(c)^2}}|$

⇒ $D=|\frac{2+(2)(3)-2(-5)-9}{\sqrt{(1)^2+(2)^2+(-2)^2}}|$

= $|\frac{2+6+10-9}{\sqrt{1+4+4}}|$

= 9/√9

D = 3 unidades.

Pregunta 4. Encuentra las ecuaciones de los planos paralelos al plano x + 2y − 2z + 8 = 0 que están a una distancia de 2 unidades del punto (2, 1, 1).

Solución:

La ecuación de un plano paralelo al plano dado es x + 2y − 2z + p = 0.

Como sabemos que la distancia entre un punto y un plano viene dada por:

$D=|\frac{ax_1+by_1+cz_1+d}{\sqrt{(a)^2+(b)^2+(c)^2}}|$

Dado, D = 2 unidades. Por eso,

$2=|\frac{2+2-2+p}{\sqrt{1+4+4}}|$

⇒ $2=|\frac{2+p}{\sqrt9}|$

Al elevar al cuadrado ambos lados, tenemos

$4=\frac{(2+p)^2}{9}$

⇒ 36 = (2 + p) ²

⇒ 2 + p = 6 o 2 + p = −6

⇒ p = 4 o p = −8

Por lo tanto, las ecuaciones de los planos requeridos son:

x + 2y − 2z + 4 = 0 y x + 2y − 2z − 8 = 0.

Pregunta 5. Demuestra que los puntos (1, 1, 1) y (−3, 0, 1) son equidistantes del plano 3x + 4y − 12z +13 = 0.

Solución:

Sabemos que la distancia entre un punto y un plano viene dada por:

$D=|\frac{ax_1+by_1+cz_1+d}{\sqrt{(a)^2+(b)^2+(c)^2}}|$

Sea D ₁ la distancia del punto (1,1,1) al plano.

⇒ $D_1=|\frac{(3)(1)+(4)(1)-(12)(1)+13}{\sqrt{(3)^2+(4)^2+(-12)^2}}|$

= 8/13 unidades

Sea D ₂ la distancia del punto.

⇒ $D_2=|\frac{(3)(-3)+(4)(0)-(12)(1)+13}{\sqrt{(3)^2+(4)^2+(-12)^2}}|$

= 8/13 unidades

Por lo tanto, los puntos son equidistantes del plano.

Pregunta 6. Encuentra la ecuación de los planos paralelos al plano x − 2y + 2z − 3 = 0 que están a una unidad de distancia del punto (2, 1, 1).

Solución:

La ecuación de un plano paralelo al plano dado es x − 2y + 2z + p = 0.

Como sabemos que la distancia entre un punto y un plano viene dada por:

$D=|\frac{ax_1+by_1+cz_1+d}{\sqrt{(a)^2+(b)^2+(c)^2}}|$

Dado, D = 1 unidades. Por eso,

$1=|\frac{1+2-2+p}{\sqrt{1+4+4}}|$

⇒ $1=|\frac{1+p}{\sqrt9}|$

Al elevar al cuadrado ambos lados, tenemos

$1=\frac{(1+p)^2}{3}$

⇒ 9 = (1 + p) ²

⇒ 1 + p = 3 o 1 + p = −3

⇒ p = 2 o p = −4

Por lo tanto, las ecuaciones de los planos requeridos son:

x − 2y + 2z + 2 = 0 y x − 2y + 2z − 4 = 0.

Pregunta 7. Encuentra la distancia del punto (2, 3, 5) desde el plano xy.

Solución:

Como sabemos la distancia del punto al plano viene dada por:

re = $|\frac{ax_1+by_1+cz_1+d}{\sqrt{(a)^2+(b)^2+(c)^2}}|$

= $|\frac{(2)(0)+(3)(0)+(5)(1)+0}{\sqrt{(0)^2+(0)^2+(1)^2}}|$

= $|\frac{0+0+5}{1}|$

D = 5 unidades

Pregunta 8. Encuentra la distancia del punto (3, 3, 3) desde el plano 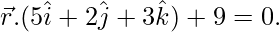$\vec{r}.(5\hat{i}+2\hat{j}+3\hat{k})+9=0.$

Solución:

Como sabemos la distancia de un punto $\vec{a}$ a un plano $\vec{r}.\vec{n}=d$ viene dada por:

re = $|\frac{\vec{a}\vec{n}-d}{|\vec{n}|}|units$

= $|\frac{(3\hat{i}+3\hat{j}+3\hat{k})(5\hat{i}+2\hat{j}+3\hat{k})+9}{\sqrt{25+4+49}}|$

= $|\frac{15+6-21+9}{\sqrt{78}}|$

D = 9/√78 unidades.

Pregunta 9. Si el producto de las distancias del punto (1, 1, 1) desde el origen y el plano x − y + z + p = 0 es 5, encuentra p.

Solución:

La distancia del punto (1, 1, 1) al origen es $\sqrt{3}.$

La distancia de (1, 1, 1) desde el plano es $|\frac{1+p}{\sqrt{3}}|$

Dado: $\sqrt{3}.|\frac{1+p}{\sqrt{3}}|=5$

⇒ |1 + p| = 5

⇒ p = 4 o −6.

Pregunta 10. Encuentra una ecuación del conjunto de todos los puntos que equidistan de los planos 3x − 4y + 12 = 6 y 4x + 3z = 7.

Solución:

$D_1=|\frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}}|$

$=|\frac{3x_1-4y_1+12z_1-6}{\sqrt{3^2+)(-4)^2+12^2}}|$

= $|\frac{3x_1-4y_1+12z_1-6}{13}|$

Ahora, $D_2=|\frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}}|$

= $|\frac{4x_1+3z_1-7}{5}|$

Dado, D ₁ = D ₂

⇒ $|\frac{3x_1-4y_1+12z_1-6}{13}|=|\frac{4x_1+3z_1-7}{5}|$

Por lo tanto, las ecuaciones se convierten en

37x ₁ + 20y ₁ − 21z ₁ − 61 = 0 y 67x ₁ + 20y ₁ + 99z ₁ − 121 = 0.

Pregunta 11. Encuentra la distancia entre el punto (7, 2, 4) y el plano determinado por los puntos A(−2, −3, 5) y C(5, 3, −3).

Solución:

Las ecuaciones del plano se dan como:

−4a − 8b + 8c = 0 y 3a − 2b + 0c = 0

Resolviendo el conjunto anterior usando el método de multiplicación cruzada, obtenemos

$\frac{a}{(-8)(0)-(-2)(8)}=\frac{b}{3(-8)-(-4)(0)}=\frac{c}{(-4)(-2)-(-3)(-8)}=p$

⇒ $\frac{a}{0+16}=\frac{b}{24+0}=\frac{c}{8+24}=p$

⇒ $\frac{a}{16}=\frac{b}{24}=\frac{c}{32}=p$

⇒ $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=p$

⇒ a = 2p, b = 3p, c = 4p

Así, la ecuación del plano se convierte en 2x + 3y + 4z − 7 = 0.

y, distancia = √29 unidades.

Pregunta 12. Un avión hace intersecciones −6, 3, 4 respectivamente en el eje de coordenadas. Encuentra la longitud de la perpendicular desde el origen en ella.

Solución:

Dado que el avión hace intersecciones −6, 3, 4, la ecuación se convierte en:

$\frac{x}{-6}+\frac{y}{3}+\frac{z}{4}=1$

Sea p la distancia de la perpendicular desde el origen al plano.

⇒ $\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$

⇒ $\frac{1}{p^2}=\frac{1}{(-6)^2}+\frac{1}{3^2}+\frac{1}{4^2}$

⇒ $\frac{1}{p^2}=\frac{4+16+9}{144}$

⇒ 1/p ² = 29/144

⇒ p ² = 144/29

⇒ p = 12/√29 unidades.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la distancia del punto desde el plano .

Pregunta 2. Demuestra que los puntos y son equidistantes del plano

Pregunta 3. Encuentra la distancia del punto (2, 3, −5) desde el plano x + 2y − 2z − 9 = 0.

Pregunta 4. Encuentra las ecuaciones de los planos paralelos al plano x + 2y − 2z + 8 = 0 que están a una distancia de 2 unidades del punto (2, 1, 1).

Pregunta 5. Demuestra que los puntos (1, 1, 1) y (−3, 0, 1) son equidistantes del plano 3x + 4y − 12z +13 = 0.

Pregunta 6. Encuentra la ecuación de los planos paralelos al plano x − 2y + 2z − 3 = 0 que están a una unidad de distancia del punto (2, 1, 1).

Pregunta 7. Encuentra la distancia del punto (2, 3, 5) desde el plano xy.

Pregunta 8. Encuentra la distancia del punto (3, 3, 3) desde el plano

Pregunta 9. Si el producto de las distancias del punto (1, 1, 1) desde el origen y el plano x − y + z + p = 0 es 5, encuentra p.

Pregunta 10. Encuentra una ecuación del conjunto de todos los puntos que equidistan de los planos 3x − 4y + 12 = 6 y 4x + 3z = 7.

Pregunta 11. Encuentra la distancia entre el punto (7, 2, 4) y el plano determinado por los puntos A(−2, −3, 5) y C(5, 3, −3).

Pregunta 12. Un avión hace intersecciones −6, 3, 4 respectivamente en el eje de coordenadas. Encuentra la longitud de la perpendicular desde el origen en ella.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la distancia del punto $2\hat{i}-\hat{j}-4\hat{k}$ desde el plano . $\vec{r}.(3\hat{i}-4\hat{j}+12\hat{k})-9=0.$

Pregunta 2. Demuestra que los puntos $\hat{i}-\hat{j}+3\hat{k}$ y $3\hat{i}+3\hat{j}+3\hat{k}$ son equidistantes del plano $\vec{r}.(5\hat{i}+2\hat{j}-7\hat{k})+9=0.$

Pregunta 8. Encuentra la distancia del punto (3, 3, 3) desde el plano $\vec{r}.(5\hat{i}+2\hat{j}+3\hat{k})+9=0.$