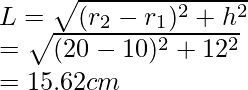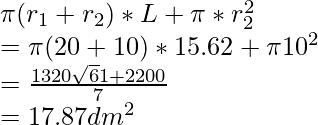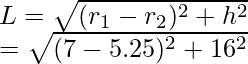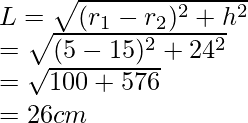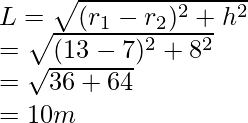Clase 10 Soluciones RD Sharma – Capítulo 16 Áreas de superficie y volúmenes – Ejercicio 16.3

Pregunta 1. Un balde tiene diámetros superior e inferior de 40 cm y 20 cm respectivamente. Halla el volumen del balde si su profundidad es de 12 cm. Además, encuentre el costo de la hojalata utilizada para fabricar el balde a razón de Rs 1.20 por dm ² .

Solución:

Dado,

Diámetro de la parte superior del balde = 40 cm

Por lo tanto,

Radio (r ₁ ) = 40/2 = 20 cm

También,

Diámetro de la parte inferior del balde = 20 cm

Por lo tanto,

Radio (r ₂ ) = 30/2 = 10 cm

Profundidad del balde (h) = 12 cm

Ahora,

Volumen de la cubeta = 1/3 π(r ₂² + r ₁² + r ₁ r ₂ )h

= π/3(20 ² + 10 ² + 20 × 10)12

⁼ 8800cm3

Ahora,

Supongamos que L es la altura inclinada del balde.

$L = \sqrt{(r_2 - r_1)^2 + h^2} \\ = \sqrt{(20-10)^2 + 12^2} \\ = 15.62 cm$

También,

Superficie total del balde =

$\pi(r_1 + r_2) * L + \pi * r_2^2 \\ = \pi (20+10) * 15.62 + \pi 10^2 \\ = \frac{1320\sqrt61 + 2200}{7} \\ = 17.87 dm^2$

Ya que,

El costo de la lámina de estaño utilizada para fabricar baldes por dm ² = Rs 1,20

Por lo tanto, el costo total de hacer un balde 17,87 dm ² = 1,20 × 17,87 = Rs 21,40

Pregunta 2. Un tronco de cono circular recto tiene un diámetro de base de 20 cm, de vértice de 12 cm y de altura de 3 cm. Halla el área de toda su superficie y volumen.

Solución:

Dado,

Sabemos,

Diámetro base del cono (d ₁ ) = 20 cm

Por lo tanto,

Radio (r ₁ ) = 20/2 cm = 10 cm

Diámetro superior del cono (d ₂ ) = 12 cm

Por lo tanto,

Radio (r ₂ ) = 12/2 cm = 6 cm

También,

Altura del cono (h) = 3 cm

Volumen del tronco de un cono circular recto = 1/3 π(r ₂² + r ₁² + r ₁ r ₂ )h

Sustituyendo los valores,

= π/3(10 ² + 6 ² + 10 × 6)3

⁼ 616cm3

Supongamos que ‘L’ es la altura inclinada del cono, entonces sabemos que

Ahora,

L = √(r ₁ – r2 ₁ ) ² + h ²

L = √(10 – 6) ² + 3 ²

L = √(16 + 9)

Resolviendo, obtenemos,

largo = 5 cm

Por lo tanto,

La altura inclinada del cono (L) = 5 cm

De este modo,

Superficie total del tronco = π(r ₁ + r ₂ ) x L + π r ₁² + π r ₂²

Sustituyendo los valores,

= π(10 + 6) × 5 + π × 10 ² + π × 6 ²

= π(80 + 100 + 36)

= π(216)

= 678,85 ^cm2

Pregunta 3. La altura inclinada del tronco de un cono es de 4 cm y los perímetros de sus extremos circulares son de 18 cm y 6 cm. Encuentre la superficie curva del tronco.

Solución:

Dado,

Altura inclinada del tronco del cono (l) = 4 cm

Supongamos que la relación de los círculos superior e inferior sea r ₁ y r ₂ respectivamente.

Y, sabemos,

Los perímetros de los extremos circulares son 18 cm y 6 cm respectivamente.

Sustituyendo los valores,

⟹ 2πr ₁ = 18 cm y 2πr ₂ = 6 cm

Resolviendo, obtenemos,

⟹ πr ₁ = 9 cm y πr ₂ = 3 cm

Ya que, sabemos,

Área de la superficie curva del tronco de un cono = π(r ₁ + r ₂ )l

= (πr ₁ +πr ₂ )l

= (9 + 3) × 4

= (12) × 4 = 48 ^cm2

Por lo tanto, el área de la superficie curva = 48 cm ²

Pregunta 4. Los perímetros de los extremos de un tronco de un cono circular recto son 44 cm y 33 cm. Si la altura del tronco es de 16 cm, encuentre su volumen, la superficie inclinada y la superficie total.

Solución:

valores dados,

Perímetro del extremo superior del cono circular= 44 cm

Ahora,

2 π r ₁ = 44

2(22/7) r ₁ = 44

Resolviendo, obtenemos,

r1 = ₇ cm

También,

Perímetro del extremo inferior del cono circular = 33 cm

2 π r ₂ = 33

2(22/7) r ₂ = 33

resolver,

r2 ₌ 21/4 cm

Ahora,

Supongamos que la altura inclinada del tronco de un cono circular recto es L

Dado,

largo = 16,1 cm

$L = \sqrt{(r_1 - r_2)^2 + h^2} \\ = \sqrt{(7-5.25)^2 + 16^2}$

Sabemos que el área de la superficie curva del cono troncocónico = π(r ₁ + r ₂ )l

Sustituyendo valores,

= π(7 + 5.25)16.1

Superficie curva del cono troncocónico = 619,65 cm ³

Y, El volumen del cono troncocónico = 1/3 π(r ₂² + r ₁² + r ₁ r ₂ )h

= 1/3 π(72 + 5.252 + (7) (5.25)) x 16

= 1898,56 cm ³

Ahora, el área de superficie total del cono troncocónico

= π(r ₁ + r ₂ ) X L + π r ₁² + π r ₂²

= π(7 + 5,25) × 16,1 + π7 ² + π5,25 ²

= π(7 + 5,25) × 16,1 + π(7 ² + 5,25 ² ) = 860,27 cm ²

Por lo tanto, el área de superficie total del cono troncocónico es de 860,27 cm ²

Pregunta 5. Si los radios de los extremos circulares de un balde cónico de 45 cm de altura son 28 cm y 7 cm, encuentra la capacidad del balde.

Solución:

Dado,

La altura del cubo cónico = 45 cm

También,

Los radios de los dos extremos del balde cónico son 28 cm y 7 cm respectivamente.

Ahora, x = 28 cm y y = 7 cm

Ahora, Volumen de la cubeta cónica = 1/3 π(x ² + y ² + xy )h

Sustituyendo los valores, obtenemos,

= 1/3 π(28 ² + 7 ² + 28 × 7)45 = 15435π

Por lo tanto, el volumen de la cubeta es 48510 cm ³ .

Pregunta 6. La altura de un cono es de 20 cm. Un pequeño cono está cortado desde la parte superior por un plano paralelo a la base. Si su volumen es 1/125 del volumen del cono original, determine a qué altura sobre la base se hace la sección.

Solución:

Sea R y r cm respectivamente el radio del cono pequeño y del cono grande.

Dado, altura del cono grande = 20 cm

Supongamos que la altura de la sección hecha es h cm

Ahora,

Cálculo de la altura del cono pequeño = (20 – h) cm

Considerando △OAB y △OCD

∠AOB = ∠COD [común]

Y como ambos ángulos miden 90 ^o

∠OAB = ∠OCD

Ahora, por similitud AA

Entonces, OAB ~ △OCD

Entonces, por CPST tenemos

OA/OC = AB/CD

Sustituyendo valores,

(20 – h)/ 20 = r/ R …… (i)

Y,

Volumen del cono pequeño = 1/125 x volumen del cono grande, es decir,

1/3 π r ² (20 – h) = 1/125 × 1/3 πR ² x 20

=>r _² / R ² = 1/125 × 20/ (20 – h) [De (i)]

=>(20 – h) ² / 20 ² = 1/125 × 20/20 – h

=>(20 – horas) ³ = 20 ³ / 125

=>20 – h = 20/5

=>20 – h = 4

Ahora,

h = 20 – 4 = 16 cm

Por lo tanto, la sección se realizó a una altura de 16 cm sobre la base.

Pregunta 7. Si los radios de los extremos circulares de un balde de 24 cm de altura son 5 y 15 cm respectivamente, encuentra el área de superficie del balde.

Solución:

Sabemos,

Altura del cubo (h) = 24 cm

Los radios de los extremos circulares del balde x e y son 5 cm y 15 cm respectivamente.

Supongamos que L es la altura inclinada del balde

$L = \sqrt{(r_1 - r_2)^2 + h^2} \\ = \sqrt{(5 - 15)^2 + 24^2} \\ = \sqrt{100+576} \\ = 26 cm$

Ahora,

El área de la superficie curva del balde está dada por = π(x+ y)l + πx ²

Sustituyendo los valores, obtenemos,

= π(5 + 15)26 + π5 ² = π(520 + 25) = 545π cm ²

Pregunta 8. Los radios de las bases circulares de un tronco de un cono circular recto son de 12 cm y 3 cm y la altura es de 12 cm. Encuentre el área de superficie total y el volumen del tronco.

Solución:

Dado,

Altura del cono troncocónico = 12 cm

Ahora,

El radio del extremo inferior (x) del tronco de cono = 12 cm

El radio del extremo superior (y) del tronco de cono = 3 cm

Supongamos que L es la altura inclinada del cono troncocónico

Ahora,

$L = \sqrt{(r_1 - r_2)^2 + h^2} \\ = \sqrt{81+144} \\ = 15 cm$

largo = 15cm

Ahora,

La superficie total del tronco de un cono = π (x + y) x L + π x ² + π y ²

Sustituyendo valores,

= π (12 + 3)15 + π12 ² + π3 ²

Resolviendo, obtenemos,

= 378 π cm ²

También,

Volumen del cono troncocónico = 1/3 π(y ² + x ² + xy )h

= 1/3 π(122 + 3 ² + 1 ² × 3) × 12

= 756π cm ³

Pregunta 9. Una tienda consiste en un tronco de cono coronado por un cono. Si los radios de los extremos del tronco son de 13 m y 7 m, la altura del tronco es de 8 m y la altura inclinada de la tapa cónica es de 12 m, encuentre la lona requerida para la tienda.

Solución:

Dado,

Los radios del cono troncocónico son 13 cm y 7 cm respectivamente.

Altura del tronco de cono, h = 8 m

Ahora,

El radio del extremo inferior (x) del tronco de cono = 13 cm

El radio del extremo superior (y) del tronco de cono = 7 cm

Supongamos que L es la altura inclinada del cono troncocónico

Ahora,

$L = \sqrt{(r_1 - r_2)^2 + h^2} \\ = \sqrt{(13 - 7)^2 + 8^2} \\ = \sqrt{36+64} \\ = 10 m$

Área de superficie curva del tronco (s ₁ ) = π(x + y) × L

= π(13 + 7) × 10

= 200 π m ²

También,

Altura inclinada de la tapa cónica = 12 m

Y,

Radio base del cono de tapa superior = 7 m

Ahora,

El área de la superficie curva del cono de la tapa superior (s ₂ ) = π *r *l

= π × 7 × 12

⁼ 264m2

Por lo tanto, la lona total necesaria para la tienda (S)

= Área de superficie curva del tronco + Área de superficie curva del cono de tapa superior

= s ₁ + s ₂

S = 200π + 264

= 892,57 m ² que es la lona necesaria para la carpa

Pregunta 10. Un recipiente de leche de 16 cm de altura está hecho de lámina de metal en forma de tronco de cono con radios de sus extremos inferior y superior de 8 cm y 20 cm respectivamente. Encuentre el costo de la leche a razón de Rs. 44 por litro que cabe en el recipiente.

Solución:

Dado,

El radio del extremo inferior (x) del tronco de cono = 8 cm

El radio del extremo superior (y) del tronco de cono = 20 cm

Altura, h = 16 cm

Ahora,

La capacidad del recipiente = Volumen de tronco de cono

que es equivalente a,

= 1/3 π(y ² + x ² + xy )h

Sustituyendo los valores,

= 1/3 π(20 ² + 8 ² + (20) (8) ) x 16

= 10459,42 cm3 ⁼ 10,46 litros

Costo de 1 litro de leche = Rs 44

Costo de 10,46 litros de leche = Rs (44 x 10,46) = Rs 460,24

Por lo tanto,

El costo de 21,98 litros de leche = Rs (25 x 21,98) = Rs 549,50

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 16 Áreas de superficie y volúmenes – Ejercicio 16.3 | Serie 1

Pregunta 1. Un balde tiene diámetros superior e inferior de 40 cm y 20 cm respectivamente. Halla el volumen del balde si su profundidad es de 12 cm. Además, encuentre el costo de la hojalata utilizada para fabricar el balde a razón de Rs 1.20 por dm ² .

Pregunta 2. Un tronco de cono circular recto tiene un diámetro de base de 20 cm, de vértice de 12 cm y de altura de 3 cm. Halla el área de toda su superficie y volumen.

Pregunta 3. La altura inclinada del tronco de un cono es de 4 cm y los perímetros de sus extremos circulares son de 18 cm y 6 cm. Encuentre la superficie curva del tronco.

Pregunta 4. Los perímetros de los extremos de un tronco de un cono circular recto son 44 cm y 33 cm. Si la altura del tronco es de 16 cm, encuentre su volumen, la superficie inclinada y la superficie total.

Pregunta 5. Si los radios de los extremos circulares de un balde cónico de 45 cm de altura son 28 cm y 7 cm, encuentra la capacidad del balde.

Pregunta 6. La altura de un cono es de 20 cm. Un pequeño cono está cortado desde la parte superior por un plano paralelo a la base. Si su volumen es 1/125 del volumen del cono original, determine a qué altura sobre la base se hace la sección.

Pregunta 7. Si los radios de los extremos circulares de un balde de 24 cm de altura son 5 y 15 cm respectivamente, encuentra el área de superficie del balde.

Pregunta 8. Los radios de las bases circulares de un tronco de un cono circular recto son de 12 cm y 3 cm y la altura es de 12 cm. Encuentre el área de superficie total y el volumen del tronco.

Pregunta 9. Una tienda consiste en un tronco de cono coronado por un cono. Si los radios de los extremos del tronco son de 13 m y 7 m, la altura del tronco es de 8 m y la altura inclinada de la tapa cónica es de 12 m, encuentre la lona requerida para la tienda.

Pregunta 10. Un recipiente de leche de 16 cm de altura está hecho de lámina de metal en forma de tronco de cono con radios de sus extremos inferior y superior de 8 cm y 20 cm respectivamente. Encuentre el costo de la leche a razón de Rs. 44 por litro que cabe en el recipiente.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Un balde tiene diámetros superior e inferior de 40 cm y 20 cm respectivamente. Halla el volumen del balde si su profundidad es de 12 cm. Además, encuentre el costo de la hojalata utilizada para fabricar el balde a razón de Rs 1.20 por dm 2 .

Pregunta 2. Un tronco de cono circular recto tiene un diámetro de base de 20 cm, de vértice de 12 cm y de altura de 3 cm. Halla el área de toda su superficie y volumen.

Pregunta 3. La altura inclinada del tronco de un cono es de 4 cm y los perímetros de sus extremos circulares son de 18 cm y 6 cm. Encuentre la superficie curva del tronco.

Pregunta 4. Los perímetros de los extremos de un tronco de un cono circular recto son 44 cm y 33 cm. Si la altura del tronco es de 16 cm, encuentre su volumen, la superficie inclinada y la superficie total.

Pregunta 5. Si los radios de los extremos circulares de un balde cónico de 45 cm de altura son 28 cm y 7 cm, encuentra la capacidad del balde.

Pregunta 6. La altura de un cono es de 20 cm. Un pequeño cono está cortado desde la parte superior por un plano paralelo a la base. Si su volumen es 1/125 del volumen del cono original, determine a qué altura sobre la base se hace la sección.

Pregunta 7. Si los radios de los extremos circulares de un balde de 24 cm de altura son 5 y 15 cm respectivamente, encuentra el área de superficie del balde.

Pregunta 8. Los radios de las bases circulares de un tronco de un cono circular recto son de 12 cm y 3 cm y la altura es de 12 cm. Encuentre el área de superficie total y el volumen del tronco.

Pregunta 9. Una tienda consiste en un tronco de cono coronado por un cono. Si los radios de los extremos del tronco son de 13 m y 7 m, la altura del tronco es de 8 m y la altura inclinada de la tapa cónica es de 12 m, encuentre la lona requerida para la tienda.

Pregunta 10. Un recipiente de leche de 16 cm de altura está hecho de lámina de metal en forma de tronco de cono con radios de sus extremos inferior y superior de 8 cm y 20 cm respectivamente. Encuentre el costo de la leche a razón de Rs. 44 por litro que cabe en el recipiente.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Un balde tiene diámetros superior e inferior de 40 cm y 20 cm respectivamente. Halla el volumen del balde si su profundidad es de 12 cm. Además, encuentre el costo de la hojalata utilizada para fabricar el balde a razón de Rs 1.20 por dm ² .