Evalúe las siguientes integrales definidas:
Pregunta 45. 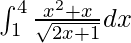
Solución:
Tenemos,
yo =
Sea 2x + 1 = t 2 , entonces tenemos,
=> 2 dx = 2t dt
=> dx = t dt
Ahora, el límite inferior es, x = 1
=> t 2 = 2x + 1
=> t 2 = 2(1) + 1
=> t 2 = 3
=> t = √3
Además, el límite superior es, x = 4
=> t 2 = 2x + 1
=> t 2 = 2(4) + 1
=> t 2 = 9
=> t = 3
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
yo =
yo =
yo = 1/4 [3 5/5 – 3 – (√3) 5/5 + √3]
yo = 1/4[243/5 – 3 – 9√3/5 + √3]
Yo = 1/4((243 – 15 – 9√3 + 5√3)/5)
Yo = 1/4[(228 – 4√3)/5]
Yo = 1/4[4(57 – √3)/5]
Yo = (57 – √3)/5
Por lo tanto, el valor de
es (57 – √3)/5.
Pregunta 46. 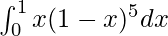
Solución:
Tenemos,
yo =
Usando el teorema del binomio en la expansión de (1 – x) 5 , obtenemos,
yo =
yo =
yo =
yo =
yo = 1/2 – 5/3 + 10/4 – 10/5 + 5/6 – 1/7
yo = 1/2 – 5/3 + 5/3 – 2 + 5/6 – 1/7
yo = 1/2 – 2 + 5/6 – 1/7
yo = 1/42
Por lo tanto, el valor de
es 1/42.
Pregunta 47. 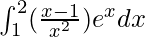
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Al usar la integración por partes, obtenemos,
yo =
yo =
yo = e x /x
Entonces obtenemos,
yo =
yo = mi 2 /2 – mi 1 /1
yo = mi 2 /2 – mi
Por lo tanto, el valor de
es e 2 /2 – e.
Pregunta 48. 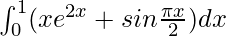
Solución:
Tenemos,
yo =
Al usar la integración por partes en la primera integral, obtenemos,
yo =
yo = xe 2x /2 – (1/2)(e 2x /2) + 2/
yo = xe 2x /2 – e 2x /4 + 2/
Entonces obtenemos,
yo =
yo = [e 2 /2 + e 2 /4 – 0 + 1/4] + 2/
yo = mi 2 /4 + 1/4 + 2/
Por lo tanto, el valor de
es e 2 /4 + 1/4 + 2/ .
Pregunta 49. 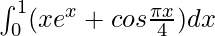
Solución:
Tenemos,
yo =
Al usar la integración por partes en la primera integral, obtenemos,
yo =
yo =
yo =
yo =
Entonces obtenemos,
yo =
yo =
yo = [e 1 (1 – 1) – e 0 (0 – 1)] + 2√2/
Yo = [0 – (-1)] + 2√2/
yo = 1 + 2√2/
Por lo tanto, el valor de
es 1 + 2√2/ .
Pregunta 50. 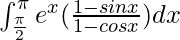
Solución:
Tenemos,
yo =
yo =
yo =
yo =
I = -e cotπ/2 + e π/2 cotπ/4
yo = 0 + e π/2 (1)
yo = mi π/2
Por lo tanto, el valor de
es e π/2 .
Pregunta 51. 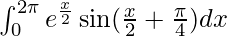
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Al usar la integración por partes en la primera integral, obtenemos,
yo =
yo =
yo =
yo = 1/√2[senπ(2e π ) – 0]
Yo = 1/√2[0 – 0]
yo = 0
Por lo tanto, el valor de
es 0.
Pregunta 52. 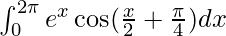
Solución:
Tenemos,
yo =
Al usar la integración por partes, obtenemos,
yo = e x cos(x/2 + π/4) + 1/2∫e x sen(x/2 + π/4)
I = e x cos(x/2 + π/4) + 1/2[ e x sin(x/2 + π/4) – 1/2 ∫e x cos(x/2 + π/4)dx]
yo = e x cos(x/2 + π/4) + 1/2e x sen(x/2 + π/4) – 1/4I
5I/4 = -3/ 2√2(e 2π + 1)
Yo = -3√2/5(e 2π + 1)
Por lo tanto, el valor de
es -3√2/5(e 2π + 1).
Pregunta 53. 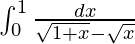
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo = 2/3[2 3/2 – 1] + 2/3[1 – 0]
yo =
yo = 2 5/2 /3
Por lo tanto, el valor de
es 2 5/2 /3.
Pregunta 54. 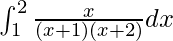
Solución:
Tenemos,
yo =
yo =
yo =
yo =
I = -log3 + log2 + 2[log4 – log3]
I = -log3 + log2 + 2[2log2 – log3]
I = -log3 + log2 + 4log2 – 2log3
I = 5log2 – 3log3
I = log2 5 – log3 3
I = log32 – log27
I = log32/27
Por lo tanto, el valor de
es log32/27.
Pregunta 55. 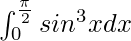
Solución:
Tenemos,
yo =
yo =
yo =
Sea cos x = t, entonces tenemos,
=> – sen x dx = dt
Ahora, el límite inferior es, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Además, el límite superior es, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
Yo = [0 – 1/3] – [0 – 1]
Yo = [-1/3] – [-1]
yo = -1/3 + 1
yo = 2/3
Por lo tanto, el valor de
es 2/3.
Pregunta 56. 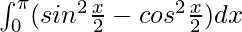
Solución:
Tenemos,
yo =
yo =
yo =
yo =
I = -sinπ + sin0
yo = 0
Por lo tanto, el valor de
es 0.
Pregunta 57. 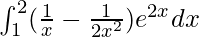
Solución:
Tenemos,
yo =
Sea 2x = t, entonces tenemos,
=> 2x dx = dt
Ahora, el límite inferior es, x = 1
=> t = 2x
=> t = 2(1)
=> t = 2
Además, el límite superior es, x = 2
=> t = 2x
=> t = 2(2)
=> t = 4
Entonces, la ecuación se convierte en,
yo =
yo =
yo =
Al usar la integración por partes en la primera integral, obtenemos,
yo =
yo =
yo =
yo = mi 4/4 – mi 2/2
Por lo tanto, el valor de
es e 4/4 – e 2/2 .
Pregunta 58. 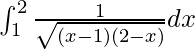
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
I = [pecado -1 (1) – senado -1 (-1)]
yo = π/2 – (-π/2)
yo = π/2 + π/2
yo = π
Por lo tanto, el valor de
es π.
Pregunta 59. Si 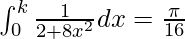 , encuentra el valor de k.
, encuentra el valor de k.
Solución:
Tenemos,
=>
=>
=>
=>
=> bronceado -1 2k/4 – bronceado -1 0 = 16
=> bronceado -1 2k/4 – 0 = 16
=> bronceado -1 2k/4 = 16
=> bronceado -1 2k =
=> 2k = bronceado
=> 2k = 1
=> k = 1/2
Por lo tanto, el valor de k es 1/2.
Pregunta 60. Si 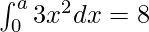 , encuentra el valor de k.
, encuentra el valor de k.
Solución:
Tenemos,
=>
=>
=>
=>
=> un 3 – 0 = 8
=> un 3 = 8
=> un = 2
Por lo tanto, el valor de a es 2.
Pregunta 61. 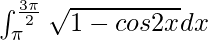
Solución:
Tenemos,
yo =
yo =
yo =
yo =
Yo = -[√2cos32 – √2cos]
Yo = -(-√2 – 0)
yo = √2
Por lo tanto, el valor de
es √2.
Pregunta 62. 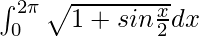
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = [-4cosπ/2 + 4cos0] + [4sinπ/2 – 4sin0]
yo = 0 + 4 + 4 – 0
yo = 8
Por lo tanto, el valor de
es 8.
Pregunta 63. 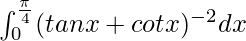
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Yo = (8 – 1/4) – (3/4(8 – 1/4) – 1/16)
yo = 8 – 1/4 – (332 – 3/16 – 1/16)
Yo = π/8 – 1/4 – (3π/32 – 1/4)
yo = π/8 – 1/4 – 3π/32 + 1/4
yo = π/8 – 3π/32
Yo = (4π – 3π)/32
yo = π/32
Por lo tanto, el valor de
es .
Pregunta 64. 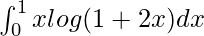
Solución:
Tenemos,
yo =
Usando la integración por partes obtenemos,
yo =
yo =
yo =
yo =
yo =
Entonces obtenemos,
yo =
I = log3/2 – 1/8log3
yo = 3/8log3
Por lo tanto, el valor de
es 3/8log3.
Pregunta 65. 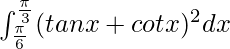
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
I = [tanπ/3 – tanπ/6] + [-cotπ/3 + cotπ/6]
Yo = [√3 – 1/√3] + [- 1/√3 – √3]
Yo = 2[√3 – 1/√3]
yo = 4/√3
Por lo tanto, el valor de
es 4/√3.
Pregunta 66. 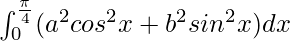
Solución:
Tenemos,
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
yo =
Por lo tanto, el valor de
es
.
Pregunta 67. 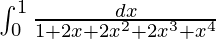
Solución:
Tenemos,
yo =
yo =
yo =
yo =
I = -log2/4 + log2/2 – 1/4 + 1/2
yo = log2/4 + 1/4
Por lo tanto, el valor de
es log2/4 + 1/4.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
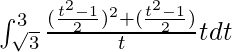
![Rendered by QuickLaTeX.com \frac{1}{4}\left[\frac{t^5}{5}-t\right]^3_{\sqrt{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9cb3a47e2c5b649a6f190d1367bb5e6_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{x^2}{2}-\frac{5x^3}{3}+\frac{10x^4}{4}-\frac{10x^5}{5}+\frac{5x^6}{6}-\frac{x^7}{7}\right]^{1}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a65957461dff0cc8e5491fa270e124c_l3.png)
![Rendered by QuickLaTeX.com \frac{xe^{2x}}{2}-\frac{1}{2}\int e^{2x}dx+\left[\frac{-cos\frac{\pi x}{2}}{\frac{\pi}{2}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60be5e9eccc6354f203d327850e1fe49_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{xe^{2x}}{2}-\frac{e^{2x}}{4}\right]^1_0+\frac{2}{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1a80263b9fbf069c4c5f2ad5ad6e579_l3.png)
![Rendered by QuickLaTeX.com xe^{x}-\int ((1)\int e^xdx)dx+ \left[\frac{sin\frac{\pi x}{4}}{\frac{\pi x}{4}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87f6a51deccf55cb84aff39019bae06e_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[sin\frac{x}{2}(2e^{\frac{x}{2}})\right]^{2\pi}_0-\int_{0}^{2\pi}e^{\frac{x}{2}}(\frac{1}{\sqrt{2}}cos\frac{x}{2})dx+\int_{0}^{2\pi}e^{\frac{x}{2}}(\frac{1}{\sqrt{2}}cos\frac{x}{2})dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54704aa9551f5825827b6c465b17de4d_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[sin\frac{x}{2}(2e^{\frac{x}{2}})\right]^{2\pi}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef494528840171d067b512d3c07bb4ce_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{2}{3}(1+x)^{\frac{3}{2}}\right]^1_0+\left[\frac{2}{3}x^{\frac{3}{2}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83103ec15687ef74fe0f42917c3c4078_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{t^2}{3}\right]^{0}_1-\left[t\right]^0_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-579eee0a8f7b85f453a7492af49c03fb_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2-\int (\frac{-1}{t^2}\int e^tdx)dx-\int_{2}^{4}\frac{e^t}{t^2}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6f08417132a2cf12e467156744de78fa_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2+\int_{2}^{4}\frac{e^t}{t^2}dt-\int_{2}^{4}\frac{e^t}{t^2}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d5ba0318179c56d53cccc6e0b15074a_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e769c55de831afc53cebadb99275d0f9_l3.png)
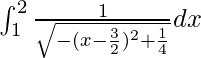
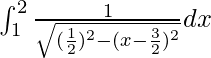
![Rendered by QuickLaTeX.com \left[\frac{tan^{-1}2x}{4}\right]_{0}^{k}=\frac{\pi}{16}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d0c3c7052508955c69b33727098a051_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{3(x^{2+1})}{2+1}\right]^a_0=8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-814c1c1c6b7c8bbe6cb228912c886733_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{3(x^{3})}{3}\right]^a_0=8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac82afd0d45be118d40a8ca9787aa6a5_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{-cos\frac{x}{4}}{\frac{1}{4}}\right]_0^{2\pi}+\left[\frac{sin\frac{x}{4}}{\frac{1}{4}}\right]_0^{2\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01085648dd622aea79608e8621c68830_l3.png)
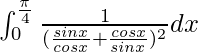
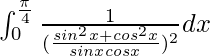
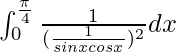
![Rendered by QuickLaTeX.com \left[\frac{x}{2}-\frac{cosxsinx}{2}\right]^{\frac{\pi}{4}}_0-\left[\frac{3}{4}(\frac{x}{2}-\frac{cosxsinx}{2})-\frac{cosxsin^3x}{4}\right]^{\frac{\pi}{4}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d39033360b58790d23d8f70bee0ea8c0_l3.png)
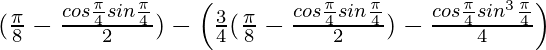
![Rendered by QuickLaTeX.com \left[\frac{x^2log(1+2x)}{2}\right]^1_0-\left[\frac{x^2}{4}-\frac{x}{4}+\frac{1}{8}log|2x+1|)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1e6888483544046b74bae20684f8cd1_l3.png)
![Rendered by QuickLaTeX.com -\left[\frac{log(x^2+1)}{4}\right]^1_0+\left[\frac{log(x+1)}{2}\right]^1_0-\left[\frac{1}{2(x+1)}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1db2b27bf504b73590a8354dd52ce2f3_l3.png)