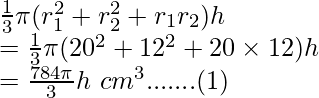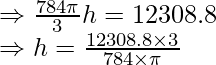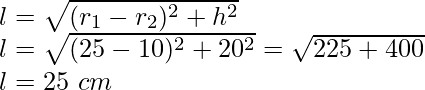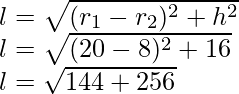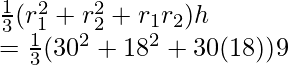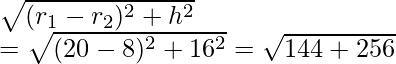Pregunta 11. Un cubo tiene la forma de un tronco de cono de 30 cm de altura con radios de sus extremos inferior y superior de 10 cm y 20 cm respectivamente. Encuentre la capacidad y el área de superficie del balde. Además, encuentre el costo de la leche que puede llenar completamente el recipiente, a razón de Rs.25 por litro.
Solución:
Sean R y r los radios de la parte superior y la base del balde respectivamente,
Sea h su altura.
Entonces, tenemos R = 20 cm, r = 10 cm, h = 30 cm
Capacidad de la cubeta = Volumen del tronco del cono
= 1/3 π(R 2 + r 2 + R r )h
= 1/3 π(20 2 + 10 2 + 20 x 10 ) x 30
= 3,14 x 10 (400 + 100 + 200)
= 21980 cm3 = 21,98 litros
Ahora,
Área de superficie del balde = CSA del balde + Área de superficie del fondo
= π l (R + r) + πr 2
Lo sabemos,
l = √h 2 + (R – r) 2
= √[30 2 + (20 – 10) 2 ] = √(900 + 100)
= √1000 = 31,62cm
Asi que,
El área de la superficie del balde = (3.14) x 31.62 x (20 + 10) + (3.14) x 10 2
= 2978.60 + 314
= 3292,60 cm2
Luego, dado que el costo de 1 litro de leche = Rs 25
Por lo tanto, el costo de 21,98 litros de leche = Rs (25 x 21,98) = Rs 549,50
Pregunta 12. Los radios de los extremos circulares de un tronco sólido de un cono son 33 cm y 27 cm y su altura inclinada es 10 cm. Halla su área de superficie total.
Solución:
Dado:
Radios de los extremos circulares superiores (r 1 ) = 20 cm
Radios del extremo circular inferior del balde (r 2 ) = 12 cm
Deje que la altura del balde sea ‘h’.
Volumen del cono troncocónico =
Capacidad/volumen dado de la cubeta = 12308,8 cm 3 —–(2)
Igualando (1) & (2)
⇒ h = 15 cm
Por lo tanto,
Altura del balde (h) = 15 cm
Sea ‘l’ la altura inclinada del balde
⇒ l 2 = (r 1 – r 2 ) 2 + h 2
⇒ yo =
⇒ yo =
⇒ largo = 17 cm
Por lo tanto,
Longitud del balde/ altura inclinada del balde (l) = 17 cm
Área de superficie curva del balde = π(r 1 + r 2 )l + πr 2 2
= π(20 + 12)17 + π(12) 2
= π(32)17 + π(12) 2
= π(9248 + 144) = 2160,32 cm2
Por lo tanto,
Superficie curvada = 2160,32 cm 2
Pregunta 13. Un cubo hecho de lámina de aluminio tiene una altura de 20 cm y sus extremos superior e inferior tienen un radio de 25 cm y 10 cm. Calcule el costo de hacer un balde si la hoja de aluminio cuesta Rs 70 por 100 cm 2 .
Solución:
Dado:
Altura del balde (h) = 20 cm
Radio superior de la cuchara (r 1 ) = 25 cm
Radio inferior de la cuchara (r 2 ) = 10 cm
Sea ‘l’ la altura inclinada del balde
Por lo tanto,
Altura inclinada del balde (l) = 25 cm
Área de superficie curva del balde = π(r 1 + r 2 )l + πr 2 2
= π(25 + 10)25 + π(10) 2
= π(35)25 + π(100) = 975π
Superficie curvada = 3061,5 cm 2
Costo de hacer un balde por 100 cm 2 = Rs 70
Costo de hacer cubeta por 3061.5 cm 2 =
= 2143,05 rupias
Por lo tanto,
Costo total de 3061,5 cm 2 = Rs 2143,05
Pregunta 14. Los radios de los extremos circulares de un tronco sólido de un cono son 33 cm y 27 cm y su altura inclinada es 10 cm. ¿Encuentra su superficie total?
Solución:
Dado:
Altura inclinada del cono troncocónico = 10 cm
Los radios de los extremos circulares del cono troncocónico son 33 y 27
r1 = 33 cm ; r2 = 27 cm
Área de superficie total de un tronco de cono sólido = π(r 1 + r 2 ) × l + πr 1 2 + πr 2 2
= π(33 + 27) × 10 + π(33) 2 + π(27) 2
= π(60) × 10 + π(33) 2 + π(27) 2
= π(600 + 1089 + 729)
= 2418πcm2
= 7599,42 cm2
Por lo tanto,
Superficie total del cono troncocónico = 7599,42 cm 2
Pregunta 15. Un balde hecho de una lámina de metal tiene forma de tronco de cono de 16 cm de altura con diámetro de sus extremos inferior y superior de 16 cm y 40 cm. Encuentre el volumen del balde. También calcule el costo del balde si el costo de la hoja de metal utilizada es de 20 rupias por 100 cm 2 .
Solución:
Dado:
Altura del cono troncocónico = 16 cm
Diámetro del extremo inferior del balde (d 1 ) = 16 cm
Radio extremo inferior (r 1 ) = 16/2 = 8 cm
Radio extremo superior (r 2 ) = 40/2 = 20 cm
Sea ‘l’ la altura inclinada del tronco de cono
largo = 20 cm
Por lo tanto,
Altura inclinada del cono troncocónico (l) = 20 cm
Volumen del cono troncocónico =
Volumen = 10449,92 cm 3
Área de la superficie curva del cono troncocónico = π(r 1 + r 2 )l + πr 2 2
= π(20 + 8)20 + π(8) 2
= π(560 + 64) = 624π cm2
Costo de la hoja de metal por 100 cm 2 = Rs 20
Costo de chapa para 624π cm 2 =
= 391,90 rupias
Por lo tanto,
Costo total del balde = Rs 391.9
Pregunta 16. Un sólido tiene la forma de un tronco de cono. Los diámetros de dos extremos circulares son 60 cm y 36 cm y la altura es 9 cm. ¿Encontrar el área de toda su superficie y volumen?
Solución:
Dado:
Altura de un cono troncocónico = 9 cm
Radio extremo inferior (r 1 ) = 60/2 cm = 30 cm
Radio extremo superior (r 2 ) = 36/2 cm = 18 cm
Sea l la altura inclinada del cono troncocónico
Volumen del cono troncocónico =
= 5292π cm 3
Volumen = 5292π cm 3
Área de superficie total del cono troncocónico = π(r 1 + r 2 ) × l + πr 1 2 + πr 2 2
= π(30 + 18)15 + π(30) 2 + π(18) 2
= π(48(15) + (30) 2 + (18) 2 )
= π(720 + 900 + 324)
= 1944πcm2
Por lo tanto,
Superficie total = 1944π cm 2
Pregunta 17. Un recipiente para leche está hecho de lámina de metal en forma de tronco de cono cuyo volumen es de 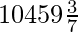 cm 3 . Los radios de su extremo circular inferior y superior son 8 cm y 20 cm. Encuentre el costo de la lámina de metal utilizada en la fabricación del contenedor a una tasa de Rs 1,40 por cm 2 .
cm 3 . Los radios de su extremo circular inferior y superior son 8 cm y 20 cm. Encuentre el costo de la lámina de metal utilizada en la fabricación del contenedor a una tasa de Rs 1,40 por cm 2 .
Solución:
Dado:
Radio extremo inferior de la cuchara (r 1 ) = 8 cm
Radio extremo superior de la cuchara (r 2 ) = 20 cm
Deje que la altura del balde sea ‘h’
V 1 =
Volumen del recipiente de leche =
V 2 =
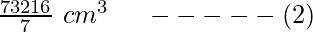
Igualando (1) y (2)
V 1 = V 2
⇒
⇒ h =
⇒ h = 16 cm
Por lo tanto,
Altura del cono troncocónico (h) = 16 cm
Sea ‘l’ la altura inclinada del cono troncocónico
yo =
largo = 20 cm
Por lo tanto,
Altura inclinada del cono troncocónico (l) = 20 cm
Área de superficie total del cono troncocónico = π(r 1 + r 2 )l + πr 1 2 + πr 2 2
= π(20 + 8)20 + π(20) 2 + π(8) 2
= π(560 + 400 + 64)
= π(960 + 64) = 1024π = 3216,99 cm2
Superficie total = 3216,99 cm 2
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA