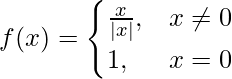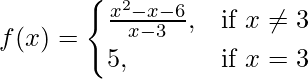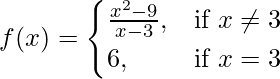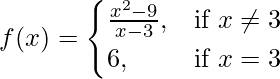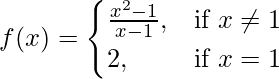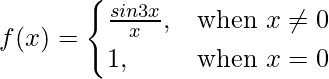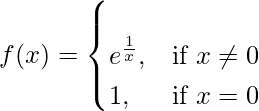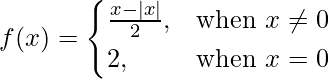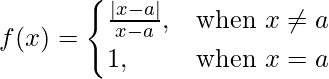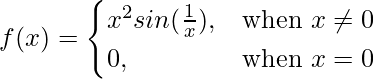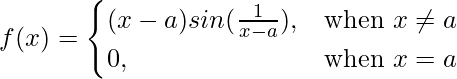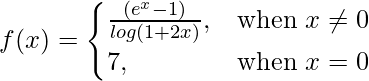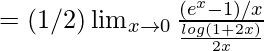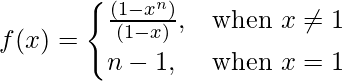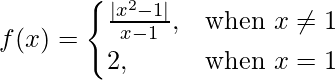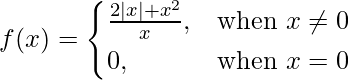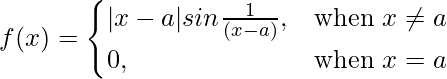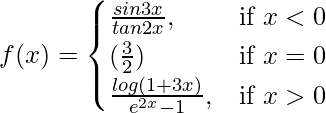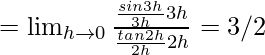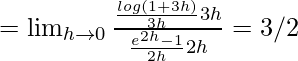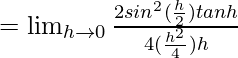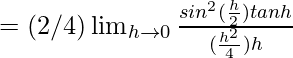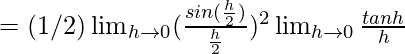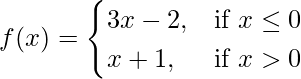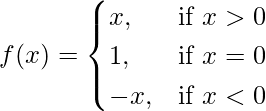Pregunta 1. Pruebe la continuidad de la siguiente función en el origen:
Solución:
Dado que
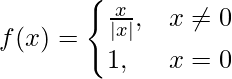
Ahora, consideremos LHL en x = 0
Ahora, consideremos RHL en x = 0
Entonces, LHL ≠ RHL
Por lo tanto, f(x) es discontinua en el origen y la discontinuidad es de primera especie.
Pregunta 2. Una función f(x) se define como 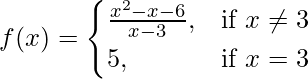 . Demuestre que f(x) es continua en x = 3.
. Demuestre que f(x) es continua en x = 3.
Solución:
Dado que
Entonces, aquí comprobamos que f(x) dada es continua en x = 3,
Ahora, consideremos LHL en x = 3
Ahora, consideremos RHL en x = 3
Entonces, f(3) = 5
LHL= RHL = f(3)
Por lo tanto, f(x) es continua en x = 3
Pregunta 3. Una función f(x) se define como
Demuestre que f(x) es continua en x = 3.
Solución:
Dado que
Entonces, aquí comprobamos que f(x) dada es continua en x = 3,
Ahora, consideremos LHL en x = 3
Ahora, consideremos RHL en x = 3
Entonces, f(3) = 6
LHL= RHL= f(3)
Por lo tanto, f(x) es continua en x = 3
Pregunta 4. 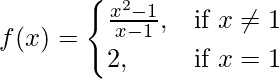
Encuentra si f(x) es continua en x = 1
Solución:
Dado que
Entonces, aquí comprobamos que f(x) dada es continua en x = 1,
Ahora, consideremos LHL en x = 1
Ahora, consideremos RHL en x = 1
Entonces, f(1) = 2
LHL= RHL = f(1)
Por lo tanto, f(x) es continua en x = 1
Pregunta 5. Si 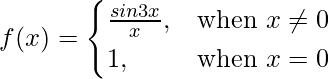
Encuentra si f(x) es continua en x = 0.
Solución:
Dado que
Entonces, aquí comprobamos que f(x) dada es continua en x = 0,
Ahora, consideremos LHL en x = 0
Ahora, consideremos RHL en x = 0
Entonces, f(0) = 1
LDH = LDH≠ f(0)
Por lo tanto, f(x) es discontinua en x = 0.
Pregunta 6. Si 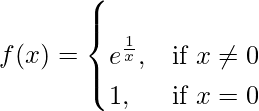
Encuentre si f es continua en x = 0.
Solución:
Dado que
Entonces, aquí comprobamos que f(x) dada es continua en x = 0,
Ahora, consideremos LHL en x = 0
Ahora, consideremos RHL en x = 0
Entonces, LHL≠ RHL
Por lo tanto, la f(x) es discontinua en x = 0.
Pregunta 7. Deja 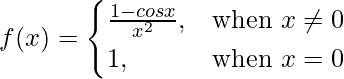
Muestre que f(x) es discontinua en x = 0.
Solución:
Dado que
Entonces, aquí comprobamos que la f(x) dada es discontinua en x = 0,
Ahora, consideremos LHL en x = 0
= 2 × 1/4 = 1/2
Ahora, consideremos RHL en x = 0
= 2 × 1/4 = 1/2
f(0) = 1
LHL= RHL ≠ f(0)
Por lo tanto, la f(x) es discontinua en x = 0.
Pregunta 8. Demuestra que 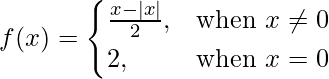 es discontinua en x = 0.
es discontinua en x = 0.
Solución:
Dado que
Entonces, aquí comprobamos que la f(x) dada es discontinua en x = 0,
Ahora, consideremos LHL en x = 0
Ahora, consideremos RHL en x = 0
f(0) = 2
Así, LHL= RHL≠ f(0)
Por lo tanto, f(x) es discontinua en x = 0.
Pregunta 9. Demuestra que 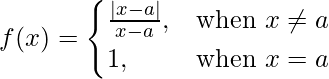 es discontinua en x = a.
es discontinua en x = a.
Solución:
Dado que
Entonces, aquí comprobamos que la f(x) dada es discontinua en x = a,
Ahora, consideremos LHL en x = a
Ahora, consideremos RHL en x = a
Por lo tanto, LHS ≠ RHL
Por lo tanto, la f(x) es discontinua en x = a.
Discuta la continuidad de las siguientes funciones en los puntos indicados:
Pregunta 10 (i). 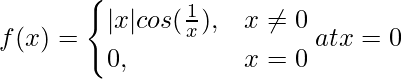
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
Consideremos LHL,
Ahora, consideremos la BSR,
f(0) = 0
Por lo tanto, LHL= RHL= f(0) = 0
Por lo tanto, f(x) es continua en x = 0.
Pregunta 10 (ii). 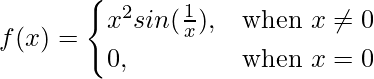 en x = 0
en x = 0
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
Consideremos LHL,
Ahora, consideremos la BSR,
f(0) = 0
Por lo tanto, LHL= RHL = f(0) = 0
Por lo tanto, f(x) es continua en x = 0.
Pregunta 10 (iii). 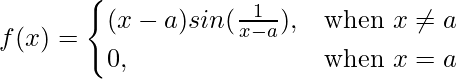 en x = un
en x = un
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = a,
Consideremos LHL,
Ahora, consideremos la BSR,
f(a) = 0
Así, LHL= RHL= f(a) = 0
Por lo tanto, f(x) es continua en x = 0.
Pregunta 10 (iv). 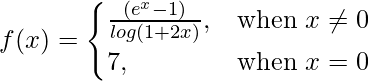 en x = 0
en x = 0
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
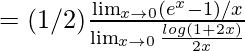
= 1/2 × 1/1 = 1/2
Y,
f(0) = 7
≠ f(0)
Por lo tanto, f(x) es discontinua en x = 0.
Pregunta 10 (v). 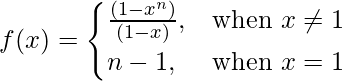 norte ∈ norte en x = 1
norte ∈ norte en x = 1
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 1,
Consideremos LHL,
Ahora, consideremos la BSR,
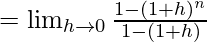
f(1) = norte – 1
Así, LHL = RHL ≠ f(1)
Por lo tanto, f(x) es discontinua en x = 1.
Pregunta 10 (vi). 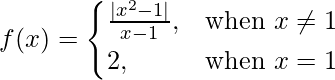 en x = 1
en x = 1
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 1,
Consideremos LHL,
Ahora, consideremos la BSR,
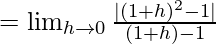
f(1) = 2
LHL= RHL = f(1) = 2
Por lo tanto, f(x) es discontinua en x = 1.
Pregunta 10 (vii). 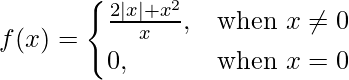 en x = 0
en x = 0
Solución:
Dado que
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
Consideremos LHL,
Consideremos la BSR,
Por lo tanto, LHL ≠ RHL
Por lo tanto, f(x) es discontinua en x = 0.
Pregunta 10 (viii). 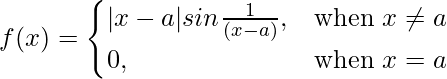 en x = un
en x = un
Solución:
Dado que,
f(x) = (x – a)sen{1/(x – a)}, x > 0
= (x – a)sen{1/(x – a)}, x < 0
= 0, x = un
Consideremos LHL,
Ahora, consideremos la BSR,
⇒
Por lo tanto, f(x) es continua en x = a.
Pregunta 11. Demuestra que 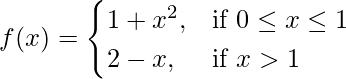 es discontinua en x = 1.
es discontinua en x = 1.
Solución:
Dado que,
Entonces, aquí comprobamos que la f(x) dada es discontinua en x = 1,
Consideremos LHL,
Ahora, consideremos la BSR,
LHL ≠ RHL
Por lo tanto, f(x) es discontinua en x = 1.
Pregunta 12. Demostrar que 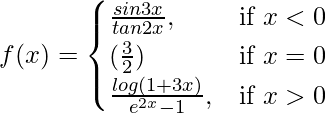 es continua en x = 0
es continua en x = 0
Solución:
Dado que,
Entonces, aquí comprobamos que f(x) dada es continua en x = 0,
Consideremos LHL,
Consideremos la BSR,
f(0) = 3/2
Por lo tanto, LHL = RHL = f(0) = 3/2
Por lo tanto, f(x) es continua en x = 0.
Pregunta 13. Encuentra el valor de ‘a’ para el cual la función f definida por
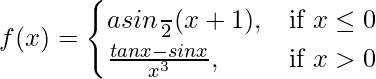 es continua en x = 0.
es continua en x = 0.
Solución:
Dado que,
Consideremos LHL,
Ahora, consideremos la BSR,
⇒
= (1/2) × 1 × 1
⇒
Si f(x) es continua en x = 0, entonces
⇒ un = 1/2
Pregunta 14. Examinar la continuidad de la función.
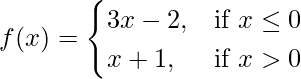 en x = 0
en x = 0
También dibuje la gráfica de esta función.
Solución:
Dado que,
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
Consideremos LHL,
Ahora, consideremos la BSR,
LhL ≠ RHL
Entonces, la f(x) es discontinua.
Pregunta 15. Discutir la continuidad de la función.
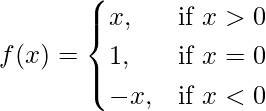 en el punto x = 0.
en el punto x = 0.
Solución:
Dado que,
Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 0,
Consideremos LHL,
Ahora, consideremos la BSR,
f(0) = 1
LHL = RHL ≠ f(0)
Por lo tanto, f(x) es discontinua en x = 0.
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA