Perspectiva de proyección en el aprendizaje automático

Antes de entrar en la perspectiva de la proyección, primero comprendamos una técnica conocida como PCA, cuál es su necesidad y dónde se usa.

Análisis de componentes principales:

Es una técnica de análisis de datos adaptativa utilizada para reducir la dimensionalidad de grandes conjuntos de datos, aumentando la interpretabilidad y minimizando las pérdidas de información y reconstrucción. En términos de aprendizaje automático, se utiliza para reducir la cantidad de parámetros (regresores) en función de cuánto contribuyen a predecir la salida para que puedan representarse gráficamente en un gráfico 2D/3D. Consideremos el siguiente modelo de regresión con 5 parámetros de entrada.

$y = x_1w_1 + x_2w_2 + x_3w_3 + x_4w_4 + x_5w_5$

where, 
y -> output (dependent variable).
x_{1, ..., x5 ->}input parameters / regressors (independent variable).
w_{1, ..., w5 ->}weights assigned to the input parameters.

No es posible representar este modelo gráficamente ya que hay 5 variables, pero solo podemos trazar datos hasta 3 dimensiones. Por lo tanto, usamos PCA que toma una entrada n donde n representa los n regresores más importantes que contribuyen a encontrar la salida y. Digamos n = 2, luego obtendremos 2 nuevos parámetros que determinarán mejor la salida y es la ecuación ahora será:

$y =x_1w_1 + x_2w_2$

Es realmente fácil representar datos en 2 dimensiones.

Perspectiva de proyección

Es una técnica utilizada en PCA que minimiza aún más el costo de reconstrucción de datos. La reconstrucción de datos simplemente significa reducir el punto de datos en dimensiones más altas a dimensiones más bajas donde es fácilmente interpretable. En este método, nos centraremos en la diferencia entre el vector de datos original x _i y el vector de datos reconstruido x _i ‘ . Para esto, encontramos un subespacio (línea) que minimiza el vector de diferencia entre el punto de datos original y su proyección como se muestra en la Fig. 1.

Fig 1: Ilustración del enfoque de proyección

Independencia lineal

Establece que siempre habrá un conjunto de vectores con los que podemos representar cada vector en el espacio vectorial al sumarlos y escalarlos. Este conjunto de vectores se llama base. En general, podemos sumar vectores y multiplicarlos con escalares como se muestra en la siguiente ecuación:

$v = \lambda_1x_1 + ... + \lambda_nx_n ;\ v \in V$

where, 
V -> vector space
v -> formed vector
x_{1...i ->} original vector
λ_{1...i ->} scalar values

Intuición

Considere una base ortogonal, B = (b ₁ , . . . , b _N ).

La base ortogonal implica b _i^T b _j = 1 iff (i = j) y 0 en caso contrario.

Según el concepto de independencia lineal, la base B se puede definir como una combinación lineal de los vectores base. (ecuación dada a continuación)

$v = \sum_{n = 1}^{N} x_nb_n \\ = \sum_{i = 1}^{I} x_ib_i + \sum_{j = I+1}^{D} x_jb_j$

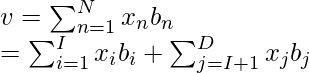
where,
v -> linear combination of basis vector existing in the higher dimension.
x -> suitable coordinates for v.

Ahora, estamos interesados en encontrar un vector v’, que existe en la dimensión inferior U (llamada subespacio principal) donde, dim(U) = I. Podemos encontrar v’ usando la siguiente ecuación:

$v' = \sum_{i = 1}^{I} y_ib_i$

where, 
v' -> new vector existing in the lower dimensions.
y -> suitable coordinates for v'.

Suponiendo que las coordenadas y _i y x _i no son idénticas entre sí.

Con base en las 2 ecuaciones anteriores, nos aseguramos de que el vector v’ que se encuentra en la dimensión inferior sea lo más similar posible al vector v en la dimensión superior.

Ahora, el objetivo es minimizar la diferencia entre el vector presente en la dimensión superior e inferior (o minimizar el error de reconstrucción). Para medir la similitud entre los vectores v y v’, encontramos la distancia euclidiana al cuadrado (también conocida como error de reconstrucción) entre ellos usando la siguiente ecuación:

$J_I = \frac{1}{N} \sum_{n = 1}^{N} ||v_n - v'_n||^2$

Considere la imagen que se muestra a continuación:

Al observar el gráfico de la izquierda, hemos mapeado las proyecciones de puntos de datos en el plano 3D. Sin embargo, no podemos segregar fácilmente los datos en grupos distintos, ya que pueden superponerse entre sí. Usando una perspectiva de proyección en PCA, podemos proyectar los puntos de datos 3D en un plano 2D. De esta manera, se vuelve más fácil interpretar los datos en grupos distintos. Esta es la gran ventaja de usar diferentes métodos de perspectiva como la perspectiva de proyección en el algoritmo PCA. Para cualquier duda/consulta comentar abajo.

Publicación traducida automáticamente

Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta