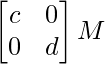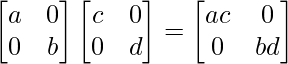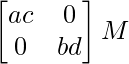Clase 12 RD Sharma Solutions – Capítulo 3 Operaciones binarias – Ejercicio 3.1

Pregunta 1. Determine si la siguiente operación define una operación binaria en el conjunto dado o no:

(i) ‘*’ sobre N definido por a * b = ab para todo a, b ∈ N.

(ii) ‘O’ en Z definido por a O b = ab para todo a, b ∈ Z.

(iii) ‘*’ en N definido por a * b = a + b – 2 para todo a, b ∈ N

(iv) ‘×6’ en S = {1, 2, 3, 4, 5} definido por a × 6 b = Resto cuando ab se divide por 6.

(v) ‘+6’ en S = {0, 1, 2, 3, 4, 5} definido por a +6 b

$=\begin{cases}a+b,\ if\ a+b<6\\a+b-6,\ if\ a+b\ge 6\end{cases}$

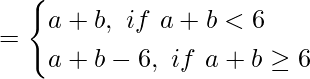
(vi) ‘⊙’ en N definido por a ⊙ b= ab + ba para todo a, b ∈ N

(vii) ‘*’ en Q definido por a * b = (a – 1)/ (b + 1) para todo a, b ∈ Q

Solución:

(i) Dado ‘*’ en N definido por a * b = a ^b para todo a, b ∈ N.

Sean a, b ∈ N. Entonces,

a ^b ∈ N [∵ ab≠0 y a, b es un entero positivo]

⇒ un * segundo ∈ norte

Por lo tanto,

un * segundo ∈ norte, ∀ un, segundo ∈ norte

Por tanto, * es una operación binaria sobre N.

(ii) Dado ‘O’ en Z definido por a O b = a ^b para todo a, b ∈ Z.

Tanto a = 3 como b = -1 pertenecen a Z.

⇒ un * segundo = 3 ^-1

= $\frac{1}{3}$ ∉Z

Por tanto, * no es una operación binaria sobre Z.

(iii) Dado ‘*’ en N definido por a * b = a + b – 2 para todo a, b ∈ N

Si a = 1 y b = 1,

a * b = a + b – 2

= 1 + 1 – 2

= 0 ∉ norte

Así, existen a = 1 y b = 1 tales que a * b ∉ N

Entonces, * no es una operación binaria en N.

(iv) Dado ‘× ₆ ‘ en S = {1, 2, 3, 4, 5} definido por a × ₆ b = Resto cuando ab se divide por 6.

Considere la tabla de composición,

x6 _{_} 1 2 3 4 5

1 1 2 3 4 5

2 2 4 0 2 4

3 3 0 3 0 3

4 4 2 0 4 2

5 5 4 3 2 1

Aquí todos los elementos de la tabla no están en S.

⇒ Para a = 2 y b = 3,

a × ₆ b = 2 × ₆ 3 = resto cuando 6 dividido por 6 = 0 ≠ S

Por lo tanto, × ₆ no es una operación binaria en S.

(v) Dado ‘+ ₆ ‘ en S = {0, 1, 2, 3, 4, 5} definido por a + ₆ b

$=\begin{casos}a+b,\ si\ a+b<6\\a+b-6,\si\ a+b\ge 6\end{casos}$

Considere la tabla de composición,

+ ₆ 0 1 2 3 4 5

0 0 1 2 3 4 5

1 1 2 3 4 5 0

2 2 3 4 5 0 1

3 3 4 5 0 1 2

4 4 5 0 1 2 3

5 5 0 1 2 3 4

Aquí todos los elementos de la tabla no están en S.

⇒ Para a = 2 y b = 3,

a × ₆ b = 2 × ₆ 3 = resto cuando 6 dividido por 6 = 0 ≠ Por lo tanto, × ₆ no es una operación binaria en S.

(vi) Dado ‘⊙’ en N definido por a ⊙ b= a ^b + b ^a para todo a, b ∈ N

Sean a, b ∈ N. Entonces,

ab, ba ∈ N

⇒ a ^b + b ^a ∈ N [∵La suma es una operación binaria en N]

⇒ un ⊙ segundo ∈ norte

Por tanto, ⊙ es una operación binaria sobre N.

(vii) Dado ‘*’ en Q definido por a * b = (a – 1)/ (b + 1) para todo a, b ∈ Q

Si a = 2 y b = -1 en Q,

un * segundo = $\frac{(a - 1)}{ (b + 1)}$

= $\frac{(2 - 1)}{ (- 1 + 1)}$

= $\frac{1}{0}$ [que no está definido]

Para a = 2 y b = -1

a * b no pertenece a Q

Entonces, * no es una operación binaria en Q.

**Pregunta 2. Determine si la definición de * dada a continuación da o no una operación binaria. En el caso de que * no sea una operación binaria dar justificación de ello.**

(i) En Z ⁺ , definido * por a * b = a – b

(ii) En Z ⁺ , defina * por a*b = ab

(iii) En R, defina * por a*b = ab ²

(iv) En Z ⁺ definir * por a * b = |a − b|

(v) En Z ⁺ definir * por a * b = a

(vi) En R, defina * por a * b = a + 4b ²

Aquí, Z ⁺ denota el conjunto de todos los números enteros no negativos.

Solución:

(i) Dado en Z ⁺ , definido * por a * b = a – b

Si a = 1 y b = 2 en Z ⁺ , entonces

un * segundo = un – segundo

= 1 – 2

= -1 ∉ Z ⁺ [porque Z ⁺ es el conjunto de enteros no negativos]

Para a = 1 y b = 2,

a * segundo ∉ Z ⁺

Por tanto, * no es una operación binaria sobre Z ⁺ .

(ii) Dado Z ⁺ , defina * por a*b = ab

Sean a, b ∈ Z ⁺

⇒ a, b ∈ Z ⁺

⇒ un * segundo ∈ Z ⁺

Por tanto, * es una operación binaria sobre R.

(iii) Dado en R, definido por a*b = ab ²

Sean a, b ∈ R

⇒ a, b ² ∈ R

⇒ ab ² ∈ R

⇒ un * segundo ∈ R

Por tanto, * es una operación binaria sobre R.

(iv) Dado en Z ⁺ definir * por a * b = |a − b|

Sean a, b ∈ Z ⁺

⇒ | un-b | ∈Z ⁺

⇒ un * segundo ∈ Z ⁺

Por lo tanto,

un * segundo ∈ Z ⁺ , ∀ un, segundo ∈ Z ⁺

Así, * es una operación binaria sobre Z ⁺ .

(v) Dado en Z ⁺ definir * por a * b = a

Sean a, b ∈ Z ⁺

⇒ un ∈ Z ⁺

⇒ un * segundo ∈ Z ⁺

Por lo tanto, a * b ∈ Z ⁺ ∀ a, b ∈ Z ⁺

Así, * es una operación binaria sobre Z ⁺ .

(vi) Dado en R, defina * por a * b = a + 4b ²

Sean a, b ∈ R

⇒ a, 4b ² ∈ R

⇒ a + 4b ² ∈ R

⇒ un * segundo ∈ R

Por lo tanto, a *b ∈ R, ∀ a, b ∈ R

Por tanto, * es una operación binaria sobre R.

**Pregunta 3. Sea * una operación binaria sobre el conjunto I de enteros, definido por a * b = 2a + b − 3. Encuentra el valor de 3 * 4.**

Solución:

Dado:

a * b = 2a + b – 3

3 * 4 = 2 (3) + 4 – 3

= 6 + 4 – 3

= 7

**Pregunta 4. ¿Está * definido en el conjunto {1, 2, 3, 4, 5} por a * b = MCM de a y ba operación binaria? Justifica tu respuesta.**

Solución:

MCM 1 2 3 4 5

1 1 2 3 4 5

2 2 2 6 4 10

3 3 5 3 12 15

4 4 4 12 4 20

5 5 10 15 20 5

En la tabla de composición dada, todos los elementos no están en el conjunto {1, 2, 3, 4, 5}.

Si consideramos a = 2 y b = 3, a * b = MCM de a y b = 6 ∉ {1, 2, 3, 4, 5}.

Por lo tanto, * no es una operación binaria en {1, 2, 3, 4, 5}.

Pregunta 5. Sea S = {a, b, c}. Encuentre el número total de operaciones binarias en S.

Solución:

El número de operaciones binarias en un conjunto con n elementos es $n^{n^2}$

Aquí, S = {a, b, c}

Número de elementos en S = 3

El número de operaciones binarias en un conjunto con 3 elementos es $3^{3^2}=3^9$

Pregunta 6. Encuentra el número total de operaciones binarias en {a, b}.

Solución:

Tenemos,

S = {a, b}

El número total de operaciones binarias en S = {a, b} en $2^{2^2}=2^4=16$

**Pregunta 7. Demostrar que la operación * en el conjunto**

M= 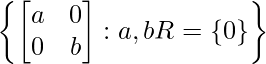$\left\{\begin{bmatrix}a&0\\0&b\end{bmatrix} : a, b ∈ R=\{0\}\right\}$ definida por A + B = AB es una operación binaria.

Solución:

Tenemos,

$\left\{\begin{bmatrix}a&0\\0&b\end{bmatrix} : a, b ∈ R=\{0\}\right\}$ y

A + B = AB para todo A, B ∈ M

Sean A =\ $\begin{bmatrix}a&0\\0&b\end{bmatrix}∈M$ y B = $\begin{bmatrix}c&0\\0&d\end{bmatrix}∈M$

Ahora AB = $\begin{bmatrix}a&0\\0&b\end{bmatrix}\begin{bmatrix}c&0\\0&d\end{bmatrix}=\begin{bmatrix}ac&0\\0&bd\end{bmatrix}$

Por lo tanto, a ∈ R, b ∈ R, c ∈ R y d ∈ R

⇒ ac ∈ R y bd ∈ R

⇒ $\begin{bmatrix}ac&0\\0&bd\end{bmatrix}∈M$

⇒ A * B ∈ METRO

Por lo tanto, el operador * define una operación binaria en M

Pregunta 8. Sea S el conjunto de todos los números racionales de la forma 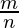$\frac{m}{n}$ **donde m ∈ Z y n = 1, 2, 3. Demostrar que * sobre S definido por a * b = ab no es una operación binaria**

Solución:

S = conjunto de números racionales de la forma $\frac{m}{n}$ donde m ∈ Z y n = 1, 2, 3

Además, a * b = ab

Sean a ∈ S y b ∈ S

⇒ ab = $\frac{35}{6}∈S$

Por lo tanto, a * b ∉ S

Por lo tanto, el operador * no define una operación binaria en S

**Pregunta 9. La operación binaria & : R × R → R se define como a*b = 2a + b**

Solución:

Se da que, a*b = 2a + b

Ahora,

(2*3) = 2 × 2 + 3

= 4 + 3

(2*3)*4 = 7*4 = 2 × 7 + 4

= 14 + 4

= 18

**Pregunta 10. Sea * una operación binaria sobre N dada por ab = MCM(a, b) para todo a, b ∈ N. Calcular 57.**

Solución:

Se da que a*b = MCM (a, b)

Ahora,

5*7 = MCM (5, 7)

= 35

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Determine si la siguiente operación define una operación binaria en el conjunto dado o no:

Pregunta 2. Determine si la definición de * dada a continuación da o no una operación binaria. En el caso de que * no sea una operación binaria dar justificación de ello.

Pregunta 3. Sea * una operación binaria sobre el conjunto I de enteros, definido por a * b = 2a + b − 3. Encuentra el valor de 3 * 4.

Pregunta 4. ¿Está * definido en el conjunto {1, 2, 3, 4, 5} por a * b = MCM de a y ba operación binaria? Justifica tu respuesta.

Pregunta 5. Sea S = {a, b, c}. Encuentre el número total de operaciones binarias en S.

Pregunta 6. Encuentra el número total de operaciones binarias en {a, b}.

Pregunta 7. Demostrar que la operación * en el conjunto

Pregunta 8. Sea S el conjunto de todos los números racionales de la forma donde m ∈ Z y n = 1, 2, 3. Demostrar que * sobre S definido por a * b = ab no es una operación binaria

Pregunta 9. La operación binaria & : R × R → R se define como a*b = 2a + b

Pregunta 10. Sea * una operación binaria sobre N dada por a*b = MCM(a, b) para todo a, b ∈ N. Calcular 5*7.

Deja una respuesta Cancelar la respuesta

**Pregunta 2. Determine si la definición de * dada a continuación da o no una operación binaria. En el caso de que * no sea una operación binaria dar justificación de ello.**

**Pregunta 3. Sea * una operación binaria sobre el conjunto I de enteros, definido por a * b = 2a + b − 3. Encuentra el valor de 3 * 4.**

**Pregunta 4. ¿Está * definido en el conjunto {1, 2, 3, 4, 5} por a * b = MCM de a y ba operación binaria? Justifica tu respuesta.**

**Pregunta 7. Demostrar que la operación * en el conjunto**

Pregunta 8. Sea S el conjunto de todos los números racionales de la forma $\frac{m}{n}$ **donde m ∈ Z y n = 1, 2, 3. Demostrar que * sobre S definido por a * b = ab no es una operación binaria**

**Pregunta 9. La operación binaria & : R × R → R se define como a*b = 2a + b**

**Pregunta 10. Sea * una operación binaria sobre N dada por ab = MCM(a, b) para todo a, b ∈ N. Calcular 57.**