Razón de la distancia entre los centros de las circunferencias y el punto de intersección de dos tangentes transversales comunes a las circunferencias

Dados dos círculos, de radios dados, tales que los círculos no se tocan entre sí. La tarea es encontrar la razón de la distancia entre los centros de los círculos y el punto de intersección de dos tangentes transversales comunes a los círculos.
Ejemplos: 
 

Input :r1 = 4, r2 = 8 
Output :1:2

Input :r1 = 5, r2 = 13
Output :5:13

Enfoque : 
 

• Sean los radios de los círculos r1 y r2 y C1 y C2 respectivamente.
• Sean P el punto de intersección de dos tangentes transversales comunes a las circunferencias, y A1 y A2 el punto de contacto de las tangentes con las circunferencias.
• En el triángulo PC1A1 y el triángulo PC2A2 ,  el
  ángulo C1A1P = ángulo C2A2P = 90 grados {la línea que une el centro del círculo con el punto de contacto forma un ángulo de 90 grados con la tangente}, 
  también el ángulo A1PC1 = ángulo A2PC2 {ángulos verticalmente opuestos son siempre iguales} 
  entonces, el ángulo A1C1P = ángulo A2C2P 
  ya que los ángulos son iguales, los triángulos PC1A1 y PC2A2 son similares.
• Entonces, debido a la similitud de los triángulos, 
  C1P/C2P = C1A1/C2A2 = r1/r2

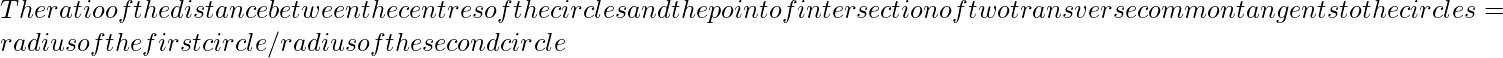
// C++ program to find the ratio
// of the distance between the centres of the circles
// and the point of intersection
// of two transverse common tangents
// to the circles which do not touch each other
 
#include <bits/stdc++.h>
using namespace std;
 
int GCD(int a, int b)
{
    return (b != 0 ? GCD(b, a % b) : a);
}
 
// Function to find the ratio
void ratiotang(int r1, int r2)
{
    cout << "The ratio is "
         << r1 / GCD(r1, r2)
         << ":"
         << r2 / GCD(r1, r2)
         << endl;
}
 
// Driver code
int main()
{
    int r1 = 4, r2 = 8;
    ratiotang(r1, r2);
    return 0;
}

// Java program to find the ratio
// of the distance between the centres of the circles
// and the point of intersection
// of two transverse common tangents
// to the circles which do not touch each other
 
import java.io.*;
 
class GFG{
 
    static int GCD(int a, int b)
    {
        return (b != 0 ? GCD(b, a % b) : a);
    }
 
    // Function to find the ratio
    static void ratiotang(int r1, int r2)
    {
        System.out.println("The ratio is "
            + r1 / GCD(r1, r2)
            + ":"
            + r2 / GCD(r1, r2));
    }
 
    // Driver code
    public static void main (String[] args)
    {
        int r1 = 4, r2 = 8;
        ratiotang(r1, r2);
    }
}
 
// This code is contributed by NamrataSrivastava1

# Python3 program to find the ratio
# of the distance between the centres of the circles
# and the point of intersection
# of two transverse common tangents
# to the circles which do not touch each other
 
def GCD(a, b):
    if(b!=0):
        return GCD(b, a%b);
    else:
        return a;
 
# Function to find the ratio
def ratiotang(r1, r2):
 
    print("The ratio is", r1 // GCD(r1, r2),
                     ":", r2 // GCD(r1, r2));
 
# Driver code
r1 = 4; r2 = 8;
ratiotang(r1, r2);
 
# This code is contributed by Code_Mech

// C# program to find the ratio
// of the distance between the centres of the circles
// and the point of intersection
// of two transverse common tangents
// to the circles which do not touch each other
using System;
 
class GFG
{
 
    static int GCD(int a, int b)
    {
        return (b != 0 ? GCD(b, a % b) : a);
    }
 
    // Function to find the ratio
    static void ratiotang(int r1, int r2)
    {
        Console.WriteLine("The ratio is "
            + r1 / GCD(r1, r2)
            + ":"
            + r2 / GCD(r1, r2));
    }
 
    // Driver code
    static public void Main ()
    {
         
        int r1 = 4, r2 = 8;
        ratiotang(r1, r2);
    }
}
 
// This code is contributed by Tushil.

<?php
// PHP program to find the ratio
// of the distance between the centres of the circles
// and the point of intersection
// of two transverse common tangents
// to the circles which do not touch each other
 
function GCD($a, $b)
{
    return ($b != 0 ? GCD($b, $a % $b) : $a);
}
 
// Function to find the ratio
function ratiotang($r1, $r2)
{
    echo "The ratio is ", $r1 / GCD($r1, $r2),
                     ":", $r2 / GCD($r1, $r2);
}
 
// Driver code
$r1 = 4;
$r2 = 8;
ratiotang($r1, $r2);
 
// This code is contributed by AnkitRai01
?>

<script>
// javascript program to find the ratio
// of the distance between the centres of the circles
// and the point of intersection
// of two transverse common tangents
// to the circles which do not touch each other
function GCD(a , b)
{
    return (b != 0 ? GCD(b, a % b) : a);
}
 
// Function to find the ratio
function ratiotang(r1 , r2)
{
    document.write("The ratio is "
        + r1 / GCD(r1, r2)
        + ":"
        + r2 / GCD(r1, r2));
}
 
// Driver code
var r1 = 4, r2 = 8;
ratiotang(r1, r2);
 
// This code is contributed by Princi Singh
</script>

The ratio is 1:2

Complejidad del tiempo: O(log(min(a, b)))

Espacio auxiliar: O(log(min(a, b)))