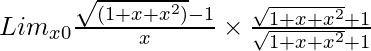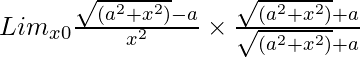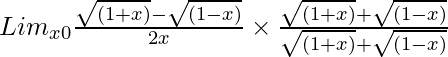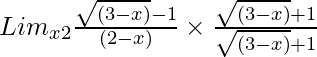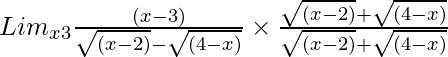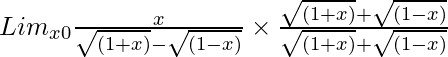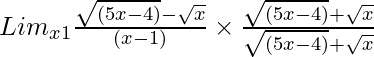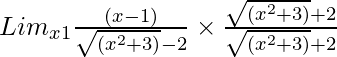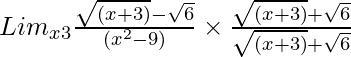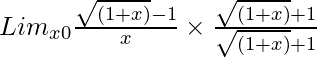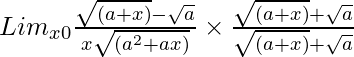Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.4

Evalúa los siguientes límites:

Pregunta 1. Lim _x→0 {√(1 + x + x ² ) – 1}/x.

Solución:

Tenemos, Lim _x→0 {√(1 + x + x ² ) – 1}/x

Encuentra el límite de la ecuación dada cuando x =>0.

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + x + x^2)} - 1}{x}\times \frac{\sqrt{1 + x + x^2}+1}{\sqrt{1 + x + x^2}+1}$

= Lim _x→0 (1 + x + x ² – 1)/{x√(1 + x + x ² ) + 1}

= Lim _x→0 {x(x + 1)}/{x√(1 + x + x ² ) + 1}

= Lim _x→0 (x + 1)/{√(1 + x + x ² ) + 1}

Ahora pon x = 0, obtenemos

= (0 + 1)/{√(1 + 0 + 0) + 1}

= 1/2

Pregunta 2. Lim _x→0 (2x)/{√(a + x) – √(a – x)}

Solución:

Tenemos, Lim _x→0 (2x)/{√(a + x) – √(a – x)}

Encuentra el límite de la ecuación dada cuando x =>0.

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{(2x)}{\sqrt{a + x} - \sqrt{a - x}} \times \frac{\sqrt{a + x} + \sqrt{a - x}}{\sqrt{a + x} + \sqrt{a - x}}$

= Lim _x→0 [2x{√(a + x) + √(a – x)}]/{(a + x) – (a – x)}

= Lim _x→0 [2x{√(a + x) + √(a – x)}]/2x

= Lim _x→0 {√(a + x) + √(a – x)}

Ahora pon x = 0, obtenemos

= √a + √a

= 2√a

Pregunta 3. Lim _x→0 {√(a ² + x ² ) – a}/x ²

Solución:

Tenemos, Lim _x→0 {√(a ² + x ² ) – a}/x ²

Encuentra el límite de la ecuación dada cuando x =>0.

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{{\sqrt{(a^2 + x^2)} - a}}{x^2} \times \frac{\sqrt{(a^2 + x^2)} + a}{\sqrt{(a^2 + x^2)} + a}$

= Lim _x→0 (a ² + x ² – a ² )/[x ² {√(a ² + x ² ) + a}]

= Lim _x→0 (x ² )/[x ² {√(a ² + x ² ) + a}]

= Lim _x→0 (1)/{√(a ² + x ² ) + a}

Ahora pon x = 0, obtenemos

= 1/(a + a)

= 1/2a

Pregunta 4. Lim _x→0 {√(1 + x) – √(1 – x)}/2x

Solución:

Tenemos, Lim _x→0 {√(1 + x) – √(1 – x)}/2x

Encuentra el límite de la ecuación dada cuando x =>0.

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + x)} - \sqrt{(1 - x)}}{2x} \times \frac{\sqrt{(1 + x)} + \sqrt{(1 - x)}}{\sqrt{(1 + x)} + \sqrt{(1 - x)}}$

= Lim _x→0 (1 + x – 1 + x)/[2x{√(1 + x) + √(1 – x)}]

= Lim _x→0 (2x)/[2x{√(1 + x) + √(1 – x)}]

= Lim _x→0 (1)/{√(1 + x) + √(1 – x)}

Ahora pon x = 0, obtenemos

= 1/(1 + 1)

= 1/2

Pregunta 5. Lim _x→2 {√(3 – x) – 1}/(2 – x)

Solución:

Tenemos, Lim _x→2 {√(3 – x) – 1}/(2 – x)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 2, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→2}\frac{\sqrt{(3 - x)} - 1}{(2 - x)} \times \frac{\sqrt{(3 - x)} + 1}{\sqrt{(3 - x)} + 1}$

= Lim _x→2 {(3 – x) – 1}/[(2 – x){√(3 – x) + 1}]

= Lim _x→2 (2 – x)/[(2 – x){√(3 – x) + 1}]

= Lim _x→2 (1)/{√(3 – x) + 1}

Ahora pon x = 2, obtenemos

= 1/{√(3 – 2) + 1}

= 1/(1 + 1)

= 1/2

Pregunta 6. Lim _x→3 (x – 3)/{√(x – 2) – √(4 – x)}

Solución:

Tenemos, Lim _x→3 (x – 3)/{√(x – 2) – √(4 – x)}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 3, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→3}\frac{(x - 3)}{\sqrt{(x - 2)} - \sqrt{(4 - x)}} \times \frac{\sqrt{(x - 2)} + \sqrt{(4 - x)}}{\sqrt{(x - 2)} + \sqrt{(4 - x)}}$

= Lim _x→3 [(x – 3){√(x – 2) + √(4 – x)}]/{(x – 2) – (4 – x)}

= Lim _x→3 [(x – 3){√(x – 2) + √(4 – x)}]/{2(x – 3)}

= Lim _x→3 {√(x – 2) + √(4 – x)}/2

Ahora pon x = 3, obtenemos

= {√(3 – 2) + √(4 – 3)}/2

= (1 + 1)/2

= 1

Pregunta 7. Lim _x→0 (x)/{√(1 + x) – √(1 – x)}

Solución:

Tenemos, Lim _x→0 (x)/{√(1 + x) – √(1 – x)}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{x}{\sqrt{(1 + x)} - \sqrt{(1 - x)}} \times \frac{\sqrt{(1 + x)} + \sqrt{(1 - x)}}{\sqrt{(1 + x)} + \sqrt{(1 - x)}}$

= Lim _x→0 [x{√(1 + x) + √(1 – x)}]/{(1 + x) – (1 – x)}

= Lim _x→0 [x{√(1 + x) + √(1 – x)}]/(2x)

= Lim _x→0 {√(1 + x) + √(1 – x)}/(2)

Ahora pon x = 0, obtenemos

= (√1 + √1)/2

= 2/2

= 1

Pregunta 8. Lim _x→1 {√(5x – 4) – √x}/(x – 1)

Solución:

Tenemos, Lim _x→1 {√(5x – 4) – √x}/(x – 1)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{\sqrt{(5x - 4)} - \sqrt{x}}{(x - 1)} \times \frac{\sqrt{(5x - 4)} + \sqrt{x}}{\sqrt{(5x - 4)} + \sqrt{x}}$

= Lim _x→1 {5x – 4 – x}/[(x – 1){√(5x – 4) + √x}]

= Lim _x→1 {4(x – 1)}/[(x – 1){√(5x – 4) + √x}]

= Lim _x→1 (4)/{√(5x – 4) + √x}

Ahora pon x = 1, obtenemos

= 4/{√(5 – 4) + √1}

= 4/(1 + 1)

= 2

Pregunta 9. Lim _x→1 (x – 1)/{√(x ² + 3) – 2}

Solución:

Tenemos, Lim _x→1 (x – 1)/{√(x ² + 3) – 2}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{(x - 1)}{\sqrt{(x^2 + 3)} - 2} \times \frac{\sqrt{(x^2 + 3)} + 2}{\sqrt{(x^2 + 3)} + 2}$

= Límite _x→1 [(x – 1){√(x ² + 3) + 2}]/{(x ² + 3) – 4}

= Lim _x→1 [(x – 1){√(x ² + 3) + 2}]/(x ² – 1)

= Límite _x→1 [(x – 1){√(x ² + 3) + 2}]/{(x – 1)(x + 1)}

= Lim _x→1 {√(x ² + 3) + 2}/{(x + 1)}

Ahora pon x = 1, obtenemos

= {√(1 + 3) + 2}/(1 + 1)

= (2 + 2)/2

= 2

Pregunta 10. Lim _x→3 {√(x + 3) – √6}/(x ² – 9)

Solución:

Tenemos, Lim _x→3 {√(x + 3) – √6}/(x ² – 9)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 3, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→3}\frac{\sqrt{(x + 3)} - \sqrt{6}}{(x^2 - 9)} \times \frac{\sqrt{(x + 3)} + \sqrt{6}}{\sqrt{(x + 3)} + \sqrt{6}}$

= Lim _x→3 {(x + 3) – 6}/[(x ² – 9){√( x+ 3) + √6}]

= Lim _x→3 (x – 3)/[(x – 3)(x + 3){√(x + 3) + √6}]

= Lim _x→3 (1)/[(x + 3){√(x + 3) + √6}]

Ahora pon x = 3, obtenemos

= $\frac{1}{(3+3)(\sqrt6+\sqrt6)}$

= $\frac{1}{(6)(2\sqrt6)}$

= 1/(12√6)

Pregunta 11. Lim _x→1 {√(5x – 4) – √x}/(x ² – 1)

Solución:

Tenemos, Lim _x→1 {√(5x – 4) – √x}/(x ² – 1)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{\sqrt{(5x - 4)} - \sqrt{x}}{(x^2 - 1)} \times \frac{\sqrt{(5x - 4)} + \sqrt{x}}{\sqrt{(5x - 4)} + \sqrt{x}}$

= Lim _x→1 {5x – 4 – x}/[(x ² – 1){√(5x – 4) + √x}]

= Lim _x→1 {4(x – 1)}/[(x – 1)(x + 1){√(5x – 4) + √x}]

= Lim _x→1 (4)/[{√(5x – 4) + √x}(x + 1)]

Ahora pon x = 1, obtenemos

= 4/[{√(5 – 4) + √1}(1 + 1)]

= 4/[(1 + 1)(1 + 1)]

= 4/4

= 1

Pregunta 12. Lim _x→0 {√(1 + x) – 1}/x

Solución:

Tenemos, Lim _x→0 {√(1 + x) – 1}/x

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + x)} - 1}{x} \times \frac{\sqrt{(1 + x)} + 1}{\sqrt{(1 + x)} + 1}$

= Lim _x→0 (1 + x – 1)/[x{√(1 + x) + 1}]

= Lim _x→0 (x)/[x{√(1 + x) + 1}]

= Lim _x→0 (1)/{√(1 + x) + 1}

Ahora pon x = 0, obtenemos

= 1/(1 + 1)

= 1/2

Pregunta 13. Lim _x→2 {√(x ² + 1) – √5}/(x – 2)

Solución:

Tenemos, Lim _x→2 {√(x ² + 1) – √5}/(x – 2)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 2, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→2}\frac{\sqrt{(x^2 + 1)} - \sqrt{5}}{(x - 2)} \times \frac{\sqrt{(x^2 + 1)} + \sqrt{5}}{\sqrt{(x^2 + 1)} + \sqrt{5}}$

= Lim _x→2 {x ² + 1 – 5}/[(x – 2){√(x ² + 1) + √5}]

= Lim _x→2 {(x ² – 4)}/[(x – 2){√(x ² + 1) + √5}]

= Lim _x→2 {(x – 2)(x + 2)}/[(x – 2){√(x ² + 1) + √5}]

= Lim _x→2 {(x + 2)}/{√(x ² + 1) + √5}

Ahora pon x = 2, obtenemos

= 4/{√(5) + √5}

= 4/(2√5)

= 2/(√5)

Pregunta 14. Lim _x→2 (x – 2)/{√x – √2}

Solución:

Tenemos, Lim _x→2 (x – 2)/{√x – √2}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 2, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→2}\frac{(x - 2)}{√x - √2} \times \frac{√x + √2}{√x + √2}$

= Lim _x→2 [(x – 2){√x + √2}]/{x – 2}

= Lim _x→2 {√x + √2}

Ahora pon x = 2, obtenemos

= √2 + √2

= 2√2

Pregunta 15. Lim _x→7 {4 – √(9 + x)}/{1 – √(8 – x)}

Solución:

Tenemos, Lim _x→7 {4 – √(9 + x)}/{1 – √(8 – x)}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 7, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $\lim_{x\to7}\frac{(4-\sqrt{9+x})(4+\sqrt{9+x})(1+\sqrt{8-x})}{(1-\sqrt{8-x})(4+\sqrt{9+x})(1+\sqrt{8-x})}$

= $\lim_{x\to7}\frac{16-(9+x)}{1-(8-x)}×\frac{(1+\sqrt{8-x})}{(4+\sqrt{9+x})}$

= $\lim_{x\to7}\frac{(7-x)}{-1(7-x)}×\frac{(1+\sqrt{8-x})}{(4+\sqrt{9+x})}$

Ahora pon x = 7, obtenemos

= -{1 + √(8 – 7)}/{4 + √(9 + 7)}

= -2/(4 + 4)

= -1/4

Pregunta 16. Lim _x→0{ √(a + x) – √a}/[x{√(a ² + ax)}]

Solución:

Tenemos,

Lim _x→0 {√(a + x) – √a}/[x{√(a ² + hacha)}]

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(a + x)} - \sqrt{a}}{x\sqrt{(a^2 + ax)}} \times \frac{\sqrt{(a + x)} + \sqrt{a}}{\sqrt{(a + x)} + \sqrt{a}}$

= Lim _x→0 {(a + x) – a}/[x{√(a ² + ax)}{√(a + x) + √a}]

= Lim _x→0 (x)/[x{√(a ² + ax)}{√(a + x) + √a}]

= Lim _x→0 (1)/[{√(a ² + ax)}{√(a + x) + √a}]

Ahora pon x = 0, obtenemos

= 1/{a.(√a + √a)}

= 1/(2a√a)

Pregunta 17. Lim _x→7 (x – 5)/{√(6x – 5) – √(4x + 5)}

Solución:

Tenemos, Lim _x→7 (x – 5)/{√(6x – 5) – √(4x + 5)}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 7, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→7}\frac{(x - 5)}{\sqrt{(6x - 5)} - \sqrt{(4x + 5)}} \times \frac{\sqrt{(6x - 5)} + \sqrt{(4x + 5)}}{\sqrt{(6x - 5)} + \sqrt{(4x + 5)}}$

= Lim _x→7 [{√(6x – 5) + √(4x + 5)}(x – 5)]/{(6x-5) – (4x + 5)}

= Límite _x→7 [{√(6x – 5) + √(4x + 5)}(x – 5)]/{2(x – 5)}

= Lim _x→7 [{√(6x – 5) + √(4x + 5)}]/(2)

Ahora pon x = 7, obtenemos

= {√(6 × 7 – 5) + √(4 × 7 + 5)}/(2)

= (5 + 5)/2

= 5

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.4 | Serie 1

Evalúa los siguientes límites:

Pregunta 1. Lim _x→0 {√(1 + x + x ² ) – 1}/x.

Pregunta 2. Lim _x→0 (2x)/{√(a + x) – √(a – x)}

Pregunta 3. Lim _x→0 {√(a ² + x ² ) – a}/x ²

Pregunta 4. Lim _x→0 {√(1 + x) – √(1 – x)}/2x

Pregunta 5. Lim _x→2 {√(3 – x) – 1}/(2 – x)

Pregunta 6. Lim _x→3 (x – 3)/{√(x – 2) – √(4 – x)}

Pregunta 7. Lim _x→0 (x)/{√(1 + x) – √(1 – x)}

Pregunta 8. Lim _x→1 {√(5x – 4) – √x}/(x – 1)

Pregunta 9. Lim _x→1 (x – 1)/{√(x ² + 3) – 2}

Pregunta 10. Lim _x→3 {√(x + 3) – √6}/(x ² – 9)

Pregunta 11. Lim _x→1 {√(5x – 4) – √x}/(x ² – 1)

Pregunta 12. Lim _x→0 {√(1 + x) – 1}/x

Pregunta 13. Lim _x→2 {√(x ² + 1) – √5}/(x – 2)

Pregunta 14. Lim _x→2 (x – 2)/{√x – √2}

Pregunta 15. Lim _x→7 {4 – √(9 + x)}/{1 – √(8 – x)}

Pregunta 16. Lim _x→0{ √(a + x) – √a}/[x{√(a ² + ax)}]

Pregunta 17. Lim _x→7 (x – 5)/{√(6x – 5) – √(4x + 5)}

Deja una respuesta Cancelar la respuesta

Evalúa los siguientes límites:

Pregunta 1. Lim x→0 {√(1 + x + x 2 ) – 1}/x.

Pregunta 2. Lim x→0 (2x)/{√(a + x) – √(a – x)}

Pregunta 3. Lim x→0 {√(a 2 + x 2 ) – a}/x 2

Pregunta 4. Lim x→0 {√(1 + x) – √(1 – x)}/2x

Pregunta 5. Lim x→2 {√(3 – x) – 1}/(2 – x)

Pregunta 6. Lim x→3 (x – 3)/{√(x – 2) – √(4 – x)}

Pregunta 7. Lim x→0 (x)/{√(1 + x) – √(1 – x)}

Pregunta 8. Lim x→1 {√(5x – 4) – √x}/(x – 1)

Pregunta 9. Lim x→1 (x – 1)/{√(x 2 + 3) – 2}

Pregunta 10. Lim x→3 {√(x + 3) – √6}/(x 2 – 9)

Pregunta 11. Lim x→1 {√(5x – 4) – √x}/(x 2 – 1)

Pregunta 12. Lim x→0 {√(1 + x) – 1}/x

Pregunta 13. Lim x→2 {√(x 2 + 1) – √5}/(x – 2)

Pregunta 14. Lim x→2 (x – 2)/{√x – √2}

Pregunta 15. Lim x→7 {4 – √(9 + x)}/{1 – √(8 – x)}

Pregunta 16. Lim x→0{ √(a + x) – √a}/[x{√(a 2 + ax)}]

Pregunta 17. Lim x→7 (x – 5)/{√(6x – 5) – √(4x + 5)}

Deja una respuesta Cancelar la respuesta

Pregunta 1. Lim _x→0 {√(1 + x + x ² ) – 1}/x.

Pregunta 2. Lim _x→0 (2x)/{√(a + x) – √(a – x)}

Pregunta 3. Lim _x→0 {√(a ² + x ² ) – a}/x ²

Pregunta 4. Lim _x→0 {√(1 + x) – √(1 – x)}/2x

Pregunta 5. Lim _x→2 {√(3 – x) – 1}/(2 – x)

Pregunta 6. Lim _x→3 (x – 3)/{√(x – 2) – √(4 – x)}

Pregunta 7. Lim _x→0 (x)/{√(1 + x) – √(1 – x)}

Pregunta 8. Lim _x→1 {√(5x – 4) – √x}/(x – 1)

Pregunta 9. Lim _x→1 (x – 1)/{√(x ² + 3) – 2}

Pregunta 10. Lim _x→3 {√(x + 3) – √6}/(x ² – 9)

Pregunta 11. Lim _x→1 {√(5x – 4) – √x}/(x ² – 1)

Pregunta 12. Lim _x→0 {√(1 + x) – 1}/x

Pregunta 13. Lim _x→2 {√(x ² + 1) – √5}/(x – 2)

Pregunta 14. Lim _x→2 (x – 2)/{√x – √2}

Pregunta 15. Lim _x→7 {4 – √(9 + x)}/{1 – √(8 – x)}

Pregunta 16. Lim _x→0{ √(a + x) – √a}/[x{√(a ² + ax)}]

Pregunta 17. Lim _x→7 (x – 5)/{√(6x – 5) – √(4x + 5)}