Dando k arreglos ordenados, cada uno de tamaño N , la tarea es fusionarlos en un solo arreglo ordenado.
Ejemplos:
Input: arr[][] = {{5, 7, 15, 18},
{1, 8, 9, 17},
{1, 4, 7, 7}}
Output: {1, 1, 4, 5, 7, 7, 7, 8, 9, 15, 17, 18}
Input: arr[][] = {{3, 2, 1}
{6, 5, 4}}
Output: {1, 2, 3, 4, 5, 6}
Requisito previo : Merge Sort
Enfoque simple: una solución simple es agregar todas las arrays una tras otra y ordenarlas.
C++14
// C++ program to merge K
// sorted arrays
#include <bits/stdc++.h>
using namespace std;
#define N 4
// Merge and sort k arrays
void merge_and_sort(
vector<int> &output, vector<vector<int>> arr,
int n, int k)
{
// Put the elements in sorted array.
for (int i = 0; i < k; i++) {
for (int j = 0; j < n; j++) {
output[(i * n) + j] = arr[i][j];
}
}
// Sort the output array
sort(output.begin(), output.end());
}
// Driver Function
int main()
{
// Input 2D-array
vector<vector<int>> arr = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
int n = N;
// Number of arrays
int k = arr.size();
// Output array
vector<int> output(n*k);
merge_and_sort(output, arr, n, k);
// Print merged array
for (int i = 0; i < n * k; i++)
cout << output[i] << " ";
return 0;
}
Java
// Java program to merge K
// sorted arrays
import java.util.*;
class GFG
{
static int N = 4;
// Merge and sort k arrays
static void merge_and_sort(int output[], int arr[][],
int n, int k)
{
// Put the elements in sorted array.
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
output[i * n + j] = arr[i][j];
}
}
// Sort the output array
Arrays.sort(output);
}
// Driver code
public static void main(String[] args)
{
// Input 2D-array
int arr[][] = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
int n = N;
// Number of arrays
int k = arr.length;
// Output array
int output[] = new int[n * k];
merge_and_sort(output, arr, n, k);
// Print merged array
for (int i = 0; i < n * k; i++)
System.out.print(output[i] + " ");
}
}
// This code is contributed by divyesh072019
Python3
# Python3 program to merge K # sorted arrays N = 4 # Merge and sort k arrays def merge_and_sort(output, arr, n, k): # Put the elements in sorted array. for i in range(k): for j in range(n): output[i * n + j] = arr[i][j]; # Sort the output array output.sort() # Driver Function if __name__=='__main__': # Input 2D-array arr = [ [ 5, 7, 15, 18 ], [ 1, 8, 9, 17 ], [ 1, 4, 7, 7 ] ]; n = N; # Number of arrays k = len(arr) # Output array output = [0 for i in range(n * k)] merge_and_sort(output, arr, n, k); # Print merged array for i in range(n * k): print(output[i], end = ' ') # This code is contributed by rutvik_56.
C#
// C# program to merge K
// sorted arrays
using System;
class GFG
{
static int N = 4;
// Merge and sort k arrays
static void merge_and_sort(int[] output, int[,] arr,
int n, int k)
{
// Put the elements in sorted array.
for (int i = 0; i < k; i++)
{
for (int j = 0; j < n; j++)
{
output[i * n + j] = arr[i,j];
}
}
// Sort the output array
Array.Sort(output);
}
// Driver code
static void Main()
{
// Input 2D-array
int[,] arr = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
int n = N;
// Number of arrays
int k = arr.GetLength(0);
// Output array
int[] output = new int[n * k];
merge_and_sort(output, arr, n, k);
// Print merged array
for (int i = 0; i < n * k; i++)
Console.Write(output[i] + " ");
}
}
// This code is contributed by divyeshrabadiya07
Javascript
<script>
// Javascript program to merge K
// sorted arrays
let N = 4;
// Merge and sort k arrays
function merge_and_sort(output, arr, n, k)
{
// Put the elements in sorted array.
for (let i = 0; i < k; i++)
{
for (let j = 0; j < n; j++)
{
output[i * n + j] = arr[i][j];
}
}
// Sort the output array
output.sort(function(a, b){return a - b});
}
// Input 2D-array
let arr = [ [ 5, 7, 15, 18 ],
[ 1, 8, 9, 17 ],
[ 1, 4, 7, 7 ] ];
let n = N;
// Number of arrays
let k = 3;
// Output array
let output = new Array(n * k);
merge_and_sort(output, arr, n, k);
// Print merged array
for (let i = 0; i < n * k; i++)
document.write(output[i] + " ");
// This code is contributed by mukesh07.
</script>
1 1 4 5 7 7 7 8 9 15 17 18
Análisis de Complejidad:
- Complejidad temporal: O(N*k*log(N*k)).
El tamaño de todos los elementos es n*k por lo que la complejidad del tiempo es O(N*k * log(N*k)) - Complejidad espacial: O(N*k).
Para almacenar la array de salida se requiere espacio O(N*k).
Solución eficiente :
enfoque: la idea se vuelve clara una vez que comenzamos a ver las k arrays como el estado intermedio del algoritmo de clasificación por fusión.
Dado que hay k arrays que ya están ordenadas, combine las k arrays. Cree una función recursiva que tomará k arrays y las dividirá en dos partes y llamará a la función recursivamente con cada mitad. Los casos base son cuando el valor de k es menor que 3.
Consulte este artículo para fusionar dos arrays en tiempo O(n).
Algoritmo:
- Inicialice la array de salida con el tamaño N*k .
- Llame a la función dividir. Sea
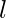 y
y 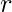 represente el rango de arrays que se fusionarán y, por lo tanto, variará entre 0 y k-1 .
represente el rango de arrays que se fusionarán y, por lo tanto, variará entre 0 y k-1 . - En cada paso, llamamos recursivamente a la mitad izquierda y derecha del rango para que se clasifiquen y almacenen en la array de salida.
- Después de eso, fusionamos la mitad izquierda y derecha. Para fusionar, necesitamos determinar el rango de índices para las mitades izquierda y derecha en la array de salida. Podemos encontrar eso fácilmente.
- La parte izquierda comenzará desde el índice l * n de la array de salida.
- De manera similar, la parte derecha comenzará desde el índice ((l + r) / 2 + 1) * n de la array de salida.
C++
// C++ program to merge K
// sorted arrays
#include<bits/stdc++.h>
#define n 4
using namespace std;
// Function to perform merge operation
void merge(int l, int r, vector<int>& output)
{
// to store the starting point
// of left and right array
int l_in = l * n, r_in
= ((l + r) / 2 + 1) * n;
// To store the size of left and
// right array
int l_c = ((l + r) / 2 - l + 1) * n;
int r_c = (r - (l + r) / 2) * n;
// array to temporarily store left
// and right array
int l_arr[l_c], r_arr[r_c];
// storing data in left array
for (int i = 0; i < l_c; i++)
l_arr[i] = output[l_in + i];
// storing data in right array
for (int i = 0; i < r_c; i++)
r_arr[i] = output[r_in + i];
// to store the current index of
// temporary left and right array
int l_curr = 0, r_curr = 0;
// to store the current index
// for output array
int in = l_in;
// two pointer merge for
// two sorted arrays
while (
l_curr + r_curr < l_c + r_c) {
if (
r_curr == r_c
|| (l_curr != l_c
&& l_arr[l_curr] < r_arr[r_curr]))
output[in]
= l_arr[l_curr],
l_curr++, in++;
else
output[in]
= r_arr[r_curr],
r_curr++, in++;
}
}
// Code to drive merge-sort and
// create recursion tree
void divide(int l, int r, vector<int>& output,
vector<vector<int>> arr)
{
if (l == r) {
/* base step to initialize the output
array before performing merge
operation */
for (int i = 0; i < n; i++)
output[l * n + i] = arr[l][i];
return;
}
// To sort left half
divide(l, (l + r) / 2,
output, arr);
// To sort right half
divide((l + r) / 2 + 1, r,
output, arr);
// Merge the left and right half
merge(l, r, output);
}
// Driver Function
int main()
{
// input 2D-array
vector<vector<int>> arr = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
// Number of arrays
int k = arr.size();
// Output array
vector<int> output(n*k);
divide(0, k - 1, output, arr);
// Print merged array
for (int i = 0; i < n * k; i++)
cout << output[i] << " ";
return 0;
}
Java
// Java program to merge
// K sorted arrays
import java.util.*;
class GFG {
static int n = 4;
// Function to perform
// merge operation
static void merge(
int l, int r, int[] output)
{
// To store the starting point
// of left and right array
int l_in = l * n, r_in
= ((l + r) / 2 + 1) * n;
// to store the size of left and
// right array
int l_c = ((l + r) / 2 - l + 1) * n;
int r_c = (r - (l + r) / 2) * n;
// array to temporarily store left
// and right array
int l_arr[] = new int[l_c],
r_arr[] = new int[r_c];
// storing data in left array
for (int i = 0; i < l_c; i++)
l_arr[i] = output[l_in + i];
// storing data in right array
for (int i = 0; i < r_c; i++)
r_arr[i] = output[r_in + i];
// to store the current index of
// temporary left and right array
int l_curr = 0, r_curr = 0;
// to store the current index
// for output array
int in = l_in;
// two pointer merge for two sorted arrays
while (l_curr + r_curr < l_c + r_c) {
if (
r_curr == r_c
|| (l_curr != l_c
&& l_arr[l_curr] < r_arr[r_curr])) {
output[in] = l_arr[l_curr];
l_curr++;
in++;
}
else {
output[in] = r_arr[r_curr];
r_curr++;
in++;
}
}
}
// Code to drive merge-sort and
// create recursion tree
static void divide(int l, int r, int[] output,
int arr[][])
{
if (l == r) {
/* base step to initialize the output
array before performing merge
operation */
for (int i = 0; i < n; i++)
output[l * n + i] = arr[l][i];
return;
}
// to sort left half
divide(l, (l + r) / 2, output, arr);
// to sort right half
divide((l + r) / 2 + 1, r, output, arr);
// merge the left and right half
merge(l, r, output);
}
// Driver Code
public static void main(String[] args)
{
// input 2D-array
int arr[][] = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
// Number of arrays
int k = arr.length;
// Output array
int[] output = new int[n * k];
divide(0, k - 1, output, arr);
// Print merged array
for (int i = 0; i < n * k; i++)
System.out.print(output[i] + " ");
}
}
/* This code contributed by PrinciRaj1992 */
Python3
# Python3 program to merge K sorted arrays n = 4 ; # Function to perform merge operation def merge(l, r, output) : # to store the starting point of # left and right array l_in = l * n ; r_in = ((l + r) // 2 + 1) * n; # to store the size of left and # right array l_c = ((l + r) // 2 - l + 1) * n; r_c = (r - (l + r) // 2) * n; # array to temporarily store left # and right array l_arr = [0] * l_c; r_arr = [0] * r_c; # storing data in left array for i in range(l_c) : l_arr[i] = output[l_in + i]; # storing data in right array for i in range(r_c) : r_arr[i] = output[r_in + i]; # to store the current index of # temporary left and right array l_curr = 0 ; r_curr = 0; # to store the current index # for output array in1 = l_in; # two pointer merge for two sorted arrays while (l_curr + r_curr < l_c + r_c) : if (r_curr == r_c or (l_curr != l_c and l_arr[l_curr] < r_arr[r_curr])) : output[in1] = l_arr[l_curr]; l_curr += 1; in1 += 1; else : output[in1] = r_arr[r_curr]; r_curr += 1; in1 += 1; # Code to drive merge-sort and # create recursion tree def divide(l, r, output, arr) : if (l == r) : # base step to initialize the output # array before performing merge # operation for i in range(n) : output[l * n + i] = arr[l][i]; return; # to sort left half divide(l, (l + r) // 2, output, arr); # to sort right half divide((l + r) // 2 + 1, r, output, arr); # merge the left and right half merge(l, r, output); # Driver code if __name__ == "__main__" : # input 2D-array arr = [[ 5, 7, 15, 18 ], [ 1, 8, 9, 17 ], [ 1, 4, 7, 7 ]]; # Number of arrays k = len(arr); # Output array output = [0] * (n * k); divide(0, k - 1, output, arr); # Print merged array for i in range(n * k) : print(output[i], end = " "); # This code is contributed by Ryuga
C#
// C# program to merge K sorted arrays
using System;
class GFG {
static int n = 4;
// Function to perform merge operation
static void merge(int l, int r, int[] output)
{
// to store the starting point of left
// and right array
int l_in = l * n, r_in = ((l + r) / 2 + 1) * n;
// to store the size of left and
// right array
int l_c = ((l + r) / 2 - l + 1) * n;
int r_c = (r - (l + r) / 2) * n;
// array to temporarily store left
// and right array
int[] l_arr = new int[l_c];
int[] r_arr = new int[r_c];
// storing data in left array
for (int i = 0; i < l_c; i++)
l_arr[i] = output[l_in + i];
// storing data in right array
for (int i = 0; i < r_c; i++)
r_arr[i] = output[r_in + i];
// to store the current index of
// temporary left and right array
int l_curr = 0, r_curr = 0;
// to store the current index
// for output array
int index = l_in;
// two pointer merge for two sorted arrays
while (l_curr + r_curr < l_c + r_c) {
if (r_curr == r_c || (l_curr != l_c && l_arr[l_curr] < r_arr[r_curr])) {
output[index] = l_arr[l_curr];
l_curr++;
index++;
}
else {
output[index] = r_arr[r_curr];
r_curr++;
index++;
}
}
}
// Code to drive merge-sort and
// create recursion tree
static void divide(int l, int r, int[] output,
int[, ] arr)
{
if (l == r) {
/* base step to initialize the output
array before performing merge
operation */
for (int i = 0; i < n; i++)
output[l * n + i] = arr[l, i];
return;
}
// to sort left half
divide(l, (l + r) / 2, output, arr);
// to sort right half
divide((l + r) / 2 + 1, r, output, arr);
// merge the left and right half
merge(l, r, output);
}
// Driver Code
public static void Main(String[] args)
{
// input 2D-array
int[, ] arr = { { 5, 7, 15, 18 },
{ 1, 8, 9, 17 },
{ 1, 4, 7, 7 } };
// Number of arrays
int k = arr.GetLength(0);
// Output array
int[] output = new int[n * k];
divide(0, k - 1, output, arr);
// Print merged array
for (int i = 0; i < n * k; i++)
Console.Write(output[i] + " ");
}
}
// This code has been contributed by 29AjayKumar
PHP
<?php
// PHP program to merge K sorted arrays
$n = 4;
// Function to perform merge operation
function merge($l, $r, &$output)
{
global $n;
// to store the starting point of left
// and right array
$l_in = $l * $n;
$r_in = ((int)(($l + $r) / 2) + 1) * $n;
// to store the size of left and
// right array
$l_c = (int)(((($l + $r) / 2) - $l + 1) * $n);
$r_c = ($r - (int)(($l + $r) / 2)) * $n;
// array to temporarily store left
// and right array
$l_arr = array_fill(0, $l_c, 0);
$r_arr = array_fill(0, $r_c, 0);
// storing data in left array
for ($i = 0; $i < $l_c; $i++)
$l_arr[$i] = $output[$l_in + $i];
// storing data in right array
for ($i = 0; $i < $r_c; $i++)
$r_arr[$i] = $output[$r_in + $i];
// to store the current index of
// temporary left and right array
$l_curr = 0;
$r_curr = 0;
// to store the current index
// for output array
$in = $l_in;
// two pointer merge for two sorted arrays
while ($l_curr + $r_curr < $l_c + $r_c)
{
if ($r_curr == $r_c || ($l_curr != $l_c &&
$l_arr[$l_curr] < $r_arr[$r_curr]))
{
$output[$in] = $l_arr[$l_curr];
$l_curr++; $in++;
}
else
{
$output[$in] = $r_arr[$r_curr];
$r_curr++; $in++;
}
}
}
// Code to drive merge-sort and
// create recursion tree
function divide($l, $r, &$output, $arr)
{
global $n;
if ($l == $r)
{
/* base step to initialize the output
array before performing merge
operation */
for ($i = 0; $i < $n; $i++)
$output[$l * $n + $i] = $arr[$l][$i];
return;
}
// to sort left half
divide($l, (int)(($l + $r) / 2), $output, $arr);
// to sort right half
divide((int)(($l + $r) / 2) + 1, $r, $output, $arr);
// merge the left and right half
merge($l, $r, $output);
}
// Driver Code
// input 2D-array
$arr = array(array( 5, 7, 15, 18 ),
array( 1, 8, 9, 17 ),
array( 1, 4, 7, 7 ));
// Number of arrays
$k = count($arr);
// Output array
$output = array_fill(0, $n * $k, 0);
divide(0, $k - 1, $output, $arr);
// Print merged array
for ($i = 0; $i < $n * $k; $i++)
print($output[$i] . " ");
// This code is contributed by mits
?>
Javascript
<script>
// Javascript program to merge K
// sorted arrays
var n = 4;
// Function to perform merge operation
function merge(l, r, output)
{
// To store the starting point
// of left and right array
var l_in = l * n,
r_in = (parseInt((l + r) / 2) + 1) * n;
// To store the size of left and
// right array
var l_c = (parseInt((l + r) / 2) - l + 1) * n;
var r_c = (r - parseInt((l + r) / 2)) * n;
// array to temporarily store left
// and right array
var l_arr = Array(l_c), r_arr = Array(r_c);
// storing data par left array
for(var i = 0; i < l_c; i++)
l_arr[i] = output[l_in + i];
// storing data par right array
for(var i = 0; i < r_c; i++)
r_arr[i] = output[r_in + i];
// to store the current index of
// temporary left and right array
var l_curr = 0, r_curr = 0;
// to store the current index
// for output array
var par = l_in;
// two pointer merge for
// two sorted arrays
while (l_curr + r_curr < l_c + r_c)
{
if (r_curr == r_c ||
(l_curr != l_c &&
l_arr[l_curr] < r_arr[r_curr]))
{
output[par] = l_arr[l_curr];
l_curr++, par++;
}
else
{
output[par] = r_arr[r_curr];
r_curr++, par++;
}
}
}
// Code to drive merge-sort and
// create recursion tree
function divide(l, r, output, arr)
{
if (l == r)
{
/* base step to initialize the output
array before performing merge
operation */
for(var i = 0; i < n; i++)
output[l * n + i] = arr[l][i];
return;
}
// To sort left half
divide(l, parseInt((l + r) / 2),
output, arr);
// To sort right half
divide(parseInt((l + r) / 2) + 1, r,
output, arr);
// Merge the left and right half
merge(l, r, output);
}
// Driver code
// Input 2D-array
var arr = [ [ 5, 7, 15, 18 ],
[ 1, 8, 9, 17 ],
[ 1, 4, 7, 7 ] ];
// Number of arrays
var k = arr.length;
// Output array
var output = Array(n * k);
divide(0, k - 1, output, arr);
// Print merged array
for(var i = 0; i < n * k; i++)
document.write(output[i] + " ");
// This code is contributed by rrrtnx
</script>
1 1 4 5 7 7 7 8 9 15 17 18
Análisis de Complejidad:
- Complejidad temporal: O(N*k*log(k)).
En cada nivel, la array de tamaño N*k se recorre una vez y el número de niveles es log(k). - Complejidad espacial: O(N*k).
Para almacenar la array de salida se requiere espacio O(N*k).
También podemos resolver este problema usando min-heap .
Publicación traducida automáticamente
Artículo escrito por DivyanshuShekhar1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA