Compruebe si todos los Nodes pueden hacerse accesibles desde un Node de un árbol mediante, como máximo, N/2 operaciones dadas

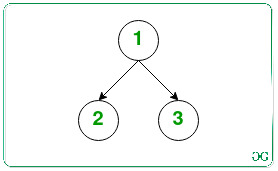
Dado un árbol dirigido que consta de N Nodes, la tarea es verificar si existe un Node en el árbol dado de modo que todos los demás Nodes sean accesibles eliminando cualquier borde dirigido del árbol y agregando otro borde dirigido entre cualquier par de Nodes en el Árbol como máximo piso (N/2) veces. Si existe tal Node, imprima «Sí» . De lo contrario, escriba “No” .

Ejemplos:

Entrada: N = 3

Salida: Sí
Explicación: 
Retire el borde 2 -> 3 e inserte un borde 1 -> 3. 

Por lo tanto, ahora se puede acceder a los dos Nodes restantes (2, 3) desde el Node 1. El
número de operaciones requeridas es 1, que es <= piso (3/2) (= 1).
Entrada: N = 5

Salida: Sí

Planteamiento: La idea para resolver este problema se basa en las siguientes observaciones:

• Cada Node debe tener al menos un Node principal, es decir, cada Node debe tener al menos 1 grado para que el árbol sea accesible desde el Node requerido.
• Se puede concluir que si cada Node tiene al menos 1 grado, entonces se puede acceder a todos los demás Nodes.
• Por lo tanto, la tarea se reduce a encontrar el número de Nodes que tienen 0 grados y verificar si es como máximo N / 2 o no.

Siga los pasos a continuación para resolver el problema: 

• Almacene el grado de entrada de cada Node en el árbol en una array auxiliar A[] de tamaño (N + 1) .
• Inicialice esta array como A[clave] = par para todos los pares (clave-valor) en el Mapa .
• Inicialice una variable, digamos contar como 0, para almacenar el número de Nodes que tienen un grado de entrada igual a 0 .
• Recorra la array A[] y cuente el número de elementos de la array con valor 0 y guárdelo en la variable count .
• Después de completar los pasos anteriores, si el valor de la cuenta es como máximo el piso (N/2) , imprima «Sí» . De lo contrario, escriba “No” .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include<bits/stdc++.h>
using namespace std;
 
void findNode(map<int, int> mp, int n)
{
     
    // Store the indegree
    // of every node
    int a[n];
 
    for(int i = 0; i < n; i++)
    {
        a[i] = mp[i + 1];
    }
 
    // Store the nodes having
    // indegree equal to 0
    int count0 = 0;
 
    // Traverse the array
    for(int i = 0; i < n; i++)
    {
         
        // If the indegree
        // of i-th node is 0
        if (a[i] == 0)
        {
             
            // Increment count0 by 1
            count0++;
        }
    }
 
    count0 -= 1;
 
    // If the number of operations
    // needed is at most floor(n/2)
    if (count0 <= floor(((double)n) /
                        ((double)2)))
    {
        cout << "Yes";
    }
 
    // Otherwise
    else
        cout << "No";
}
 
// Driver Code
int main()
{
     
    // Given number of nodes
    int N = 3;
 
    // Given Directed Tree
    map<int, int> mp;
    mp[1] = 0;
    mp[2] = 2;
    mp[3] = 0;
 
    findNode(mp, N);
}
 
// This code is contributed by SURENDRA_GANGWAR

// Java program for the above approach
import java.io.*;
import java.util.HashMap;
 
class GFG {
 
    // Function to check if there is a
    // node in tree from where all other
    // nodes are accessible or not
    public static void
    findNode(HashMap<Integer, Integer> map,
             int n)
    {
 
        // Store the indegree
        // of every node
        int[] a = new int[n];
 
        for (int i = 0; i < n; i++) {
            a[i] = map.getOrDefault(i + 1, 0);
        }
 
        // Store the nodes having
        // indegree equal to 0
        int count0 = 0;
 
        // Traverse the array
        for (int i = 0; i < n; i++) {
 
            // If the indegree
            // of i-th node is 0
            if (a[i] == 0) {
 
                // Increment count0 by 1
                count0++;
            }
        }
 
        count0 -= 1;
 
        // If the number of operations
        // needed is at most floor(n/2)
        if (count0
            <= Math.floor(((double)n)
                          / ((double)2))) {
            System.out.println("Yes");
        }
 
        // Otherwise
        else
            System.out.println("No ");
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        // Given number of nodes
        int N = 3;
 
        // Given Directed Tree
        HashMap<Integer, Integer> map
            = new HashMap<>();
 
        map.put(1, 0);
        map.put(2, 2);
        map.put(3, 0);
 
        findNode(map, N);
    }
}

# python 3 program for the above approach
 
 
def findNode(mp, n):
 
    # Store the indegree
    # of every node
    a = [0]*n
 
    for i in range(n):
 
        a[i] = mp[i + 1]
 
    # Store the nodes having
    # indegree equal to 0
    count0 = 0
 
    # Traverse the array
    for i in range(n):
 
        # If the indegree
        # of i-th node is 0
        if (a[i] == 0):
 
            # Increment count0 by 1
            count0 += 1
 
    count0 -= 1
 
    # If the number of operations
    # needed is at most floor(n/2)
    if (count0 <= (n) /
            (2)):
 
        print("Yes")
 
    # Otherwise
    else:
        print("No")
 
 
# Driver Code
if __name__ == "__main__":
 
    # Given number of nodes
    N = 3
 
    # Given Directed Tree
    mp = {}
    mp[1] = 0
    mp[2] = 2
    mp[3] = 0
 
    findNode(mp, N)

// C# program for the above approach
using System;
using System.Collections.Generic;
 
public class GFG{
  
    // Function to check if there is a
    // node in tree from where all other
    // nodes are accessible or not
    public static void
    findNode(Dictionary<int, int> map,
             int n)
    {
 
        // Store the indegree
        // of every node
        int[] a = new int[n];
 
        for (int i = 0; i < n; i++) {
            if(map.ContainsKey(i+1))
            a[i] = map[i + 1];
            else
            a[i] = 0;
        }
 
        // Store the nodes having
        // indegree equal to 0
        int count0 = 0;
 
        // Traverse the array
        for (int i = 0; i < n; i++) {
 
            // If the indegree
            // of i-th node is 0
            if (a[i] == 0) {
 
                // Increment count0 by 1
                count0++;
            }
        }
 
        count0 -= 1;
 
        // If the number of operations
        // needed is at most floor(n/2)
        if (count0
            <= Math.Floor(((double)n)
                          / ((double)2))) {
            Console.WriteLine("Yes");
        }
 
        // Otherwise
        else
            Console.WriteLine("No ");
    }
  
    static public void Main ()
    {
       
   // Given number of nodes
        int N = 3;
 
        // Given Directed Tree
        Dictionary<int, int> map
            = new Dictionary<int, int>();
 
       map[1]= 0;
        map[2] = 2;
        map[3] = 0;
 
        findNode(map, N);
    }
}
 
// This code is contributed by offbeat

<script>
 
// Javascript program for the above approach
 
function findNode(mp, n)
{
     
    // Store the indegree
    // of every node
    var a = new Array(n);
     
    var i;
    for(i = 0; i < n; i++)
    {
        a[i] = mp[i + 1];
    }
 
    // Store the nodes having
    // indegree equal to 0
    var count0 = 0;
 
    // Traverse the array
    for(i = 0; i < n; i++)
    {
         
        // If the indegree
        // of i-th node is 0
        if (a[i] == 0)
        {
             
            // Increment count0 by 1
            count0++;
        }
    }
 
    count0 -= 1;
 
    // If the number of operations
    // needed is at most floor(n/2)
    if (count0 <= parseInt(n/2))
    {
        document.write("Yes");
    }
 
    // Otherwise
    else
        document.write("No");
}
 
// Driver Code
  
    // Given number of nodes
    var N = 3;
 
    // Given Directed Tree
    var mp = new Map();
    mp.set(1,0);
    mp.set(2,2);
    mp.set(3,0);
    mp[1] = 0;
    mp[2] = 2;
    mp[3] = 0;
 
    findNode(mp, N);
 
</script>

Yes

Complejidad temporal: O(N)
Espacio auxiliar: O(N)