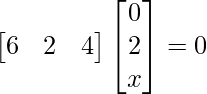
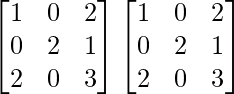
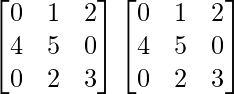
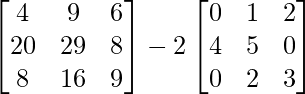
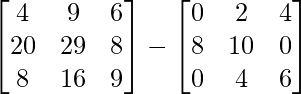
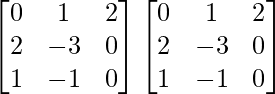
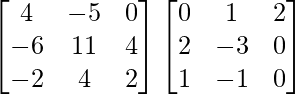
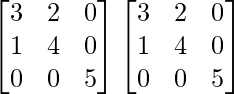
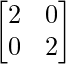
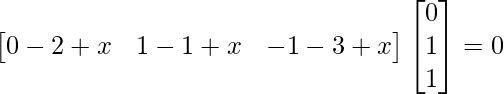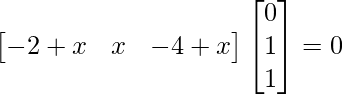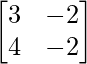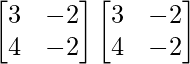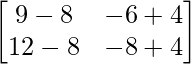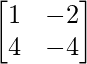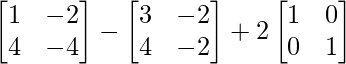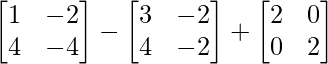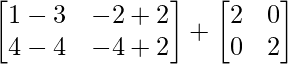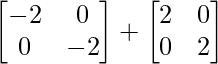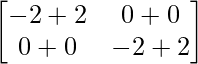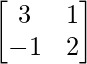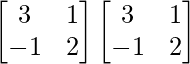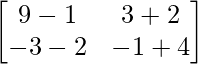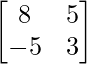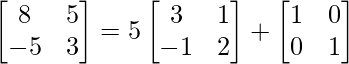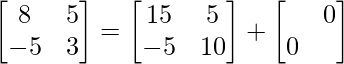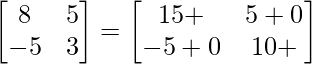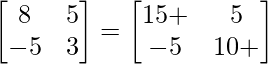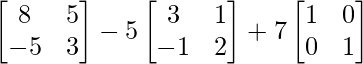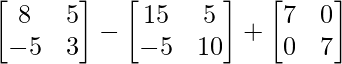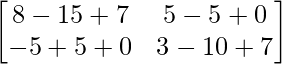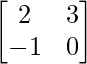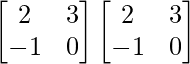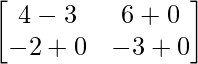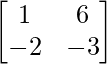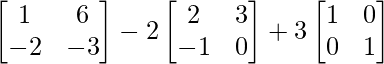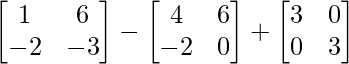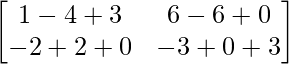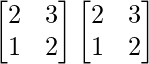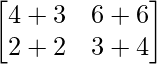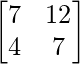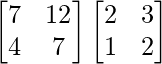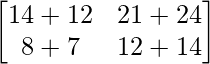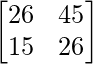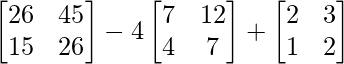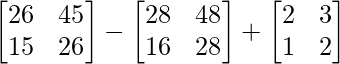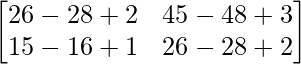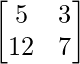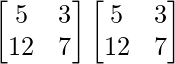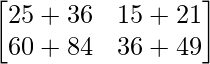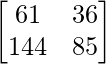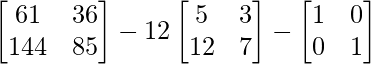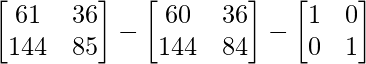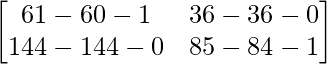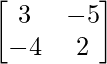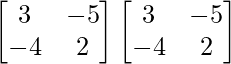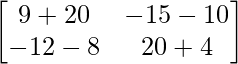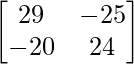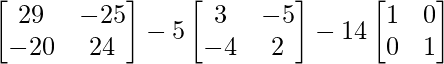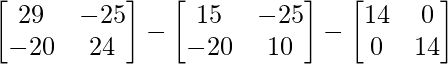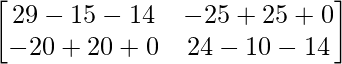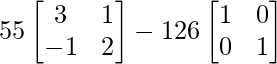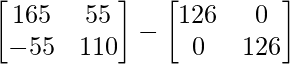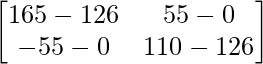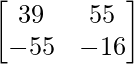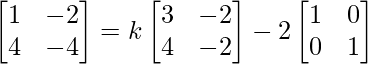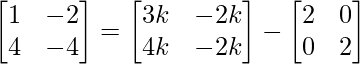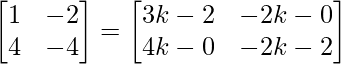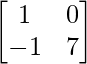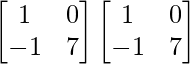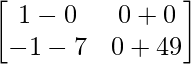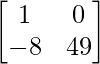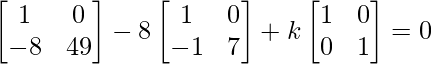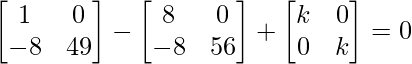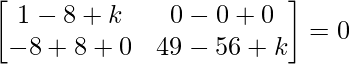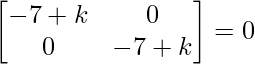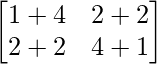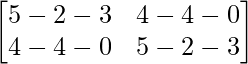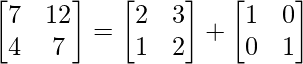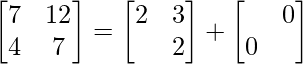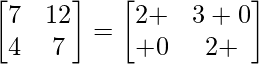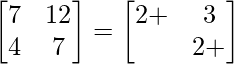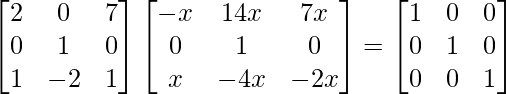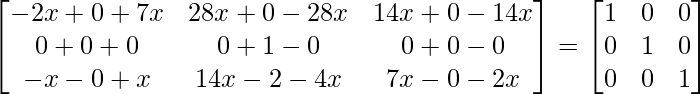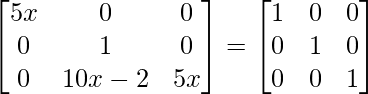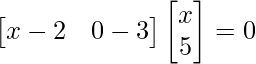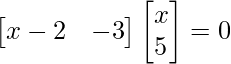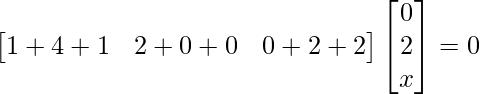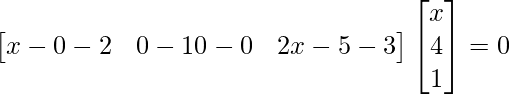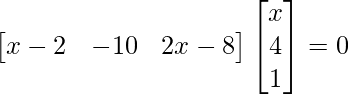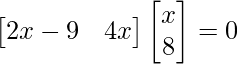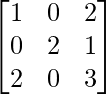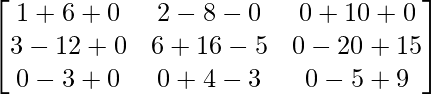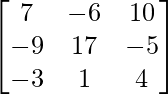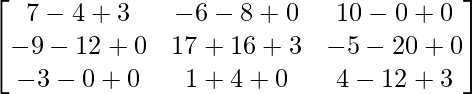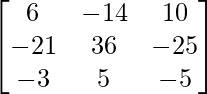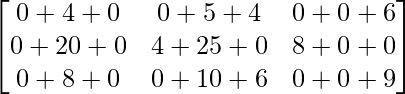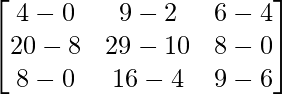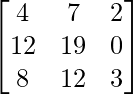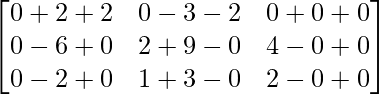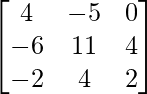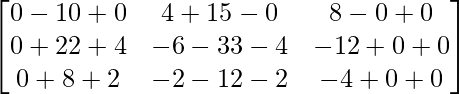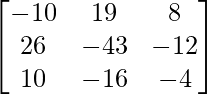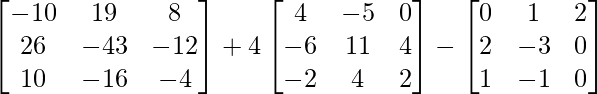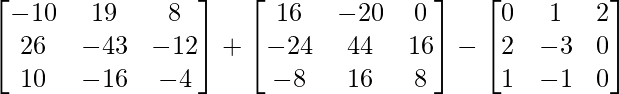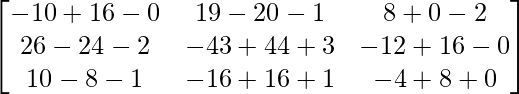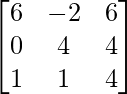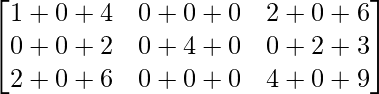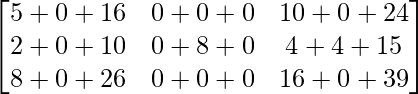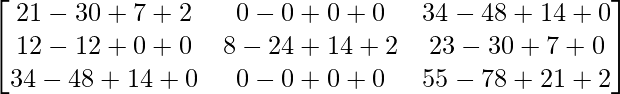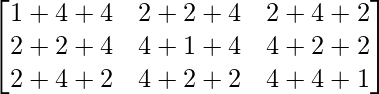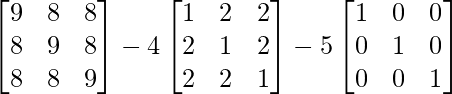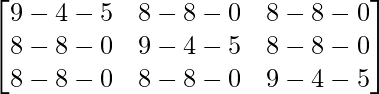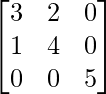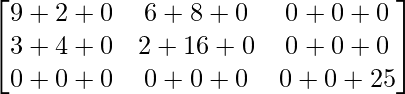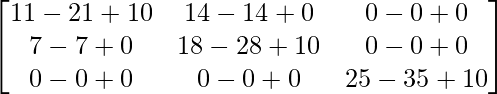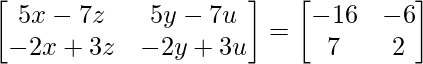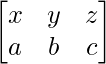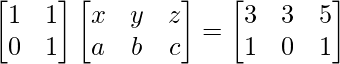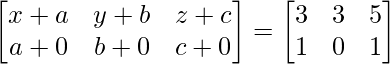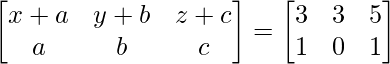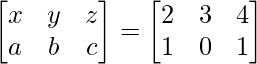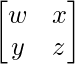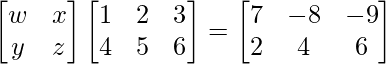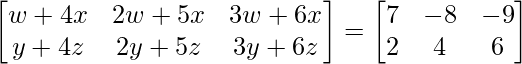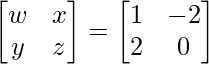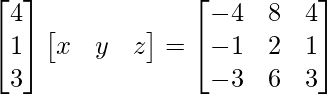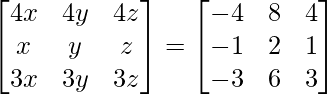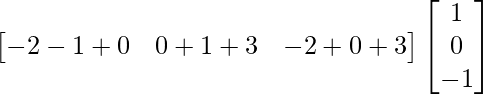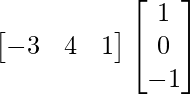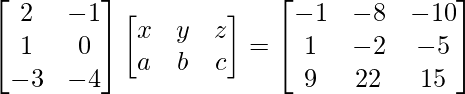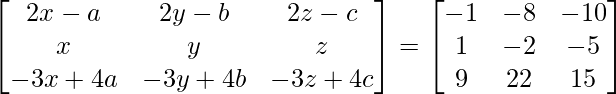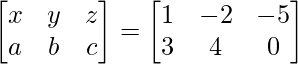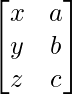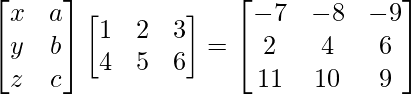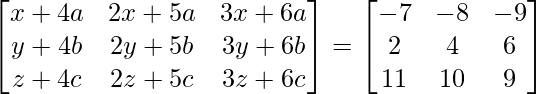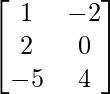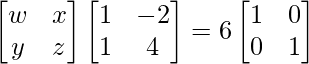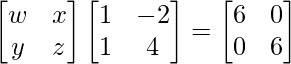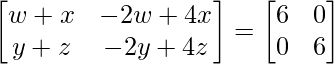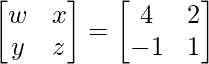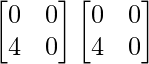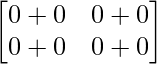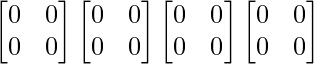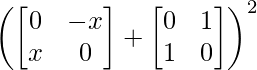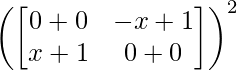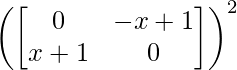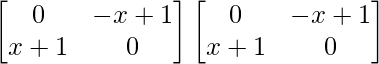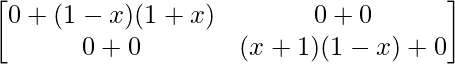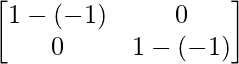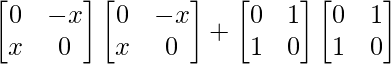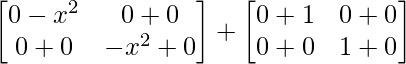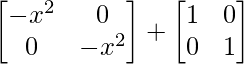Clase 12 Soluciones RD Sharma – Capítulo 5 Álgebra de Arrays – Ejercicio 5.3

Pregunta 26. Si 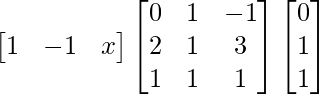$\begin{bmatrix}1 & -1 & x\end{bmatrix}\begin{bmatrix}0 & 1 & -1\\2 & 1 & 3\\1 & 1 & 1\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}$ = 0, encuentra x.

Solución:

Tenemos,

=> $\begin{bmatrix}1 & -1 & x\end{bmatrix}\begin{bmatrix}0 & 1 & -1\\2 & 1 & 3\\1 & 1 & 1\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}$ = 0

=> $\begin{bmatrix}0-2+x & 1-1+x & -1-3+x\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}=0$

=> $\begin{bmatrix}-2+x & x & -4+x\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}=0$

=> $\begin{bmatrix}0+x-4+x\end{bmatrix}=0$

=> 2x – 4 = 0

=> 2x = 4

=> x = 2

Por lo tanto, el valor de x es 2.

Pregunta 27. Si A = 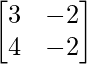$\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces demuestre que A ² – A + 2I = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$

un ² = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$

= $\begin{bmatrix}9-8 & -6+4\\12-8 & -8+4\end{bmatrix}$

= $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix}$

IZQ = A ² – A + 2I

= $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix}-\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}+2\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix}-\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}+\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

= $\begin{bmatrix}1-3 & -2+2\\4-4 & -4+2\end{bmatrix}+\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

= $\begin{bmatrix}-2 & 0\\0 & -2\end{bmatrix}+\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

= $\begin{bmatrix}-2+2 & 0+0\\0+0 & -2+2\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 28. Si A = 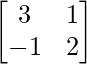$\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces encuentra λ tal que A ² = 5A + λI.

Solución:

Tenemos,

un = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

un ² = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

= $\begin{bmatrix}9-1 & 3+2\\-3-2 & -1+4\end{bmatrix}$

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}$

Se nos da,

=> A ² = 5A + λI

=> $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}=5\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}+λ\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

=> $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}=\begin{bmatrix}15 & 5\\-5 & 10\end{bmatrix}+\begin{bmatrix}λ & 0\\0 & λ\end{bmatrix}$

=> $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}=\begin{bmatrix}15+λ & 5+0\\-5+0 & 10+λ\end{bmatrix}$

=> $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}=\begin{bmatrix}15+λ & 5\\-5 & 10+λ\end{bmatrix}$

Al comparar ambos lados, obtenemos

=> 8 = 15 + λ

=> λ = –7

Por lo tanto, el valor de λ es –7.

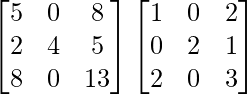
Pregunta 29. Si A = 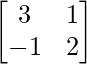$\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , demuestre que A ² – 5A + 7I ₂ = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

A2 = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

= $\begin{bmatrix}9-1 & 3+2\\-3-2 & -1+4\end{bmatrix}$

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}$

IZQ = A ² – 5A + 7I ₂

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}-5\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}+7\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}-\begin{bmatrix}15 & 5\\-5 & 10\end{bmatrix}+\begin{bmatrix}7 & 0\\0 & 7\end{bmatrix}$

= $\begin{bmatrix}8-15+7 & 5-5+0\\-5+5+0 & 3-10+7\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 30. Si A = 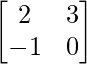$\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}$ , demuestre que A ² – 2A + 3I ₂ = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}$

un ² = $\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}$

= $\begin{bmatrix}4-3 & 6+0\\-2+0 & -3+0\end{bmatrix}$

= $\begin{bmatrix}1 & 6\\-2 & -3\end{bmatrix}$

IZQ = A ² – 2A + 3I ₂

= $\begin{bmatrix}1 & 6\\-2 & -3\end{bmatrix}-2\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}+3\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}1 & 6\\-2 & -3\end{bmatrix}-\begin{bmatrix}4 & 6\\-2 & 0\end{bmatrix}+\begin{bmatrix}3 & 0\\0 & 3\end{bmatrix}$

= $\begin{bmatrix}1-4+3 & 6-6+0\\-2+2+0 & -3+0+3\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 31. Demuestra que la array A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ satisface la ecuación A ³ – 4A ² + A = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

un ² = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

= $\begin{bmatrix}4+3 & 6+6\\2+2 & 3+4\end{bmatrix}$

= $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}$

UN ³ = UN ² . A

= $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

= $\begin{bmatrix}14+12 & 21+24\\8+7 & 12+14\end{bmatrix}$

= $\begin{bmatrix}26 & 45\\15 & 26\end{bmatrix}$

IZQ = A ³ – 4A ² + A

= $\begin{bmatrix}26 & 45\\15 & 26\end{bmatrix}-4\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}+\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

= $\begin{bmatrix}26 & 45\\15 & 26\end{bmatrix}-\begin{bmatrix}28 & 48\\16 & 28\end{bmatrix}+\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

= $\begin{bmatrix}26-28+2 & 45-48+3\\15-16+1 & 26-28+2\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 32. Demostrar que la array A = 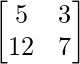$\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}$ es raíz de la ecuación A ² – 12A – I = 0

Solución:

Tenemos,

un = $\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}$

un ² = $\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}$

= $\begin{bmatrix}25+36 & 15+21\\60+84 & 36+49\end{bmatrix}$

= $\begin{bmatrix}61 & 36\\144 & 85\end{bmatrix}$

IZQ = A ² – 12A – I

= $\begin{bmatrix}61 & 36\\144 & 85\end{bmatrix}-12\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}-\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}61 & 36\\144 & 85\end{bmatrix}-\begin{bmatrix}60 & 36\\144 & 84\end{bmatrix}-\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}61-60-1 & 36-36-0\\144-144-0 & 85-84-1\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 33. Si A = 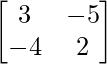$\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}$ encuentra A ² – 5A – 14I.

Solución:

Tenemos,

un = $\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}$

un ² = $\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}$

= $\begin{bmatrix}9+20 & -15-10\\-12-8 & 20+4\end{bmatrix}$

= $\begin{bmatrix}29 & -25\\-20 & 24\end{bmatrix}$

A ² – 5A – 14I = $\begin{bmatrix}29 & -25\\-20 & 24\end{bmatrix}-5\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}-14\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}29 & -25\\-20 & 24\end{bmatrix}-\begin{bmatrix}15 & -25\\-20 & 10\end{bmatrix}-\begin{bmatrix}14 & 0\\0 & 14\end{bmatrix}$

= $\begin{bmatrix}29-15-14 & -25+25+0\\-20+20+0 & 24-10-14\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

Pregunta 34. Si A = 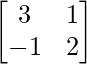$\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , encuentra A ² – 5A + 7I = 0. Usa esto para encontrar A ⁴ .

Solución:

Tenemos,

un = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

un ² = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$

= $\begin{bmatrix}9-1 & 3+2\\-3-2 & -1+4\end{bmatrix}$

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}$

IZQ = A ² – 5A + 7I = 0

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}-5\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}+7\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}8 & 5\\-5 & 3\end{bmatrix}-\begin{bmatrix}15 & 5\\-5 & 10\end{bmatrix}+\begin{bmatrix}7 & 0\\0 & 7\end{bmatrix}$

= $\begin{bmatrix}8-15+7 & 5-5+0\\-5+5+0 & 3-10+7\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Ahora tenemos A ² – 5A + 7I = 0

=> A ² = 5A – 7I

=> A ⁴ = (5A – 7I) (5A – 7I)

=> A ⁴ = 25A ² – 35AI – 35AI + 49I

=> A ⁴ = 25A ² – 70AI + 49I

=> A ⁴ = 25 (5A – 7I) – 70AI + 49I

=> A ⁴ = 125A – 175I – 70A + 49I

=> A ⁴ = 55A – 126I

=> Un ⁴ = $55\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}-126\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

=> Un ⁴ = $\begin{bmatrix}165 & 55\\-55 & 110\end{bmatrix}-\begin{bmatrix}126 & 0\\0 & 126\end{bmatrix}$

=> Un ⁴ = $\begin{bmatrix}165-126 & 55-0\\-55-0 & 110-126\end{bmatrix}$

=> Un ⁴ = $\begin{bmatrix}39 & 55\\-55 & -16\end{bmatrix}$

Pregunta 35. Si A = 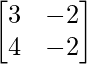$\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ , encuentra k tal que A ² = kA – 2I ₂ .

Solución:

Tenemos,

un = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$

un ² = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$

= $\begin{bmatrix}9-8 & -6+4\\12-8 & -8+4\end{bmatrix}$

= $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix}$

Se nos da,

=> A ² = kA – 2I ₂

=> $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix} = k\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}-2\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

=> $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix} = \begin{bmatrix}3k & -2k\\4k & -2k\end{bmatrix}-\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

=> $\begin{bmatrix}1 & -2\\4 & -4\end{bmatrix} = \begin{bmatrix}3k-2 & -2k-0\\4k-0 & -2k-2\end{bmatrix}$

Al comparar ambos lados, obtenemos

=> 3k – 2 = 1

=> 3k = 3

=> k = 1

Por lo tanto, el valor de k es 1.

Pregunta 36. Si A = 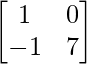$\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}$ , encuentra k tal que A ² – 8A + kI = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}$

un ² = $\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}$

= $\begin{bmatrix}1-0 & 0+0\\-1-7 & 0+49\end{bmatrix}$

= $\begin{bmatrix}1 & 0\\-8 & 49\end{bmatrix}$

Se nos da,

=> A ² – 8A + kI = 0

=> $\begin{bmatrix}1 & 0\\-8 & 49\end{bmatrix}-8\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}+k\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}=0$

=> $\begin{bmatrix}1 & 0\\-8 & 49\end{bmatrix}-\begin{bmatrix}8 & 0\\-8 & 56\end{bmatrix}+\begin{bmatrix}k & 0\\0 & k\end{bmatrix}=0$

=> $\begin{bmatrix}1-8+k & 0-0+0\\-8+8+0 & 49-56+k\end{bmatrix} = 0$

=> $\begin{bmatrix}-7+k & 0\\0 & -7+k\end{bmatrix} = 0$

Al comparar ambos lados, obtenemos

=> –k + 7 = 0

=> k = 7

Por lo tanto, el valor de k es 7.

Pregunta 37. Si A = 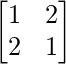$\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}$ y f(x) = x ² – 2x – 3, demuestre que f(A) = 0.

Solución:

Tenemos,

A = $\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}$ y f(x) = x ² – 2x – 3

un ² = $\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}$

= $\begin{bmatrix}1+4 & 2+2\\2+2 & 4+1\end{bmatrix}$

= $\begin{bmatrix}5 & 4\\4 & 5\end{bmatrix}$

LHS = f(A) = A ² – 2A – 3I ₂

= $\begin{bmatrix}5 & 4\\4 & 5\end{bmatrix}-2\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}+3\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}5 & 4\\4 & 5\end{bmatrix}-\begin{bmatrix}2 & 4\\4 & 2\end{bmatrix}+\begin{bmatrix}3 & 0\\0 & 3\end{bmatrix}$

= $\begin{bmatrix}5-2-3 & 4-4-0\\4-4-0 & 5-2-3\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 38. Si A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , encuentre λ, μ para que A ² = λA + μI.

Solución:

Tenemos,

un = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

un ² = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$

= $\begin{bmatrix}4+3 & 6+6\\2+2 & 3+4\end{bmatrix}$

= $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}$

Se nos da,

=> A ² = λA + μI

=> $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}=λ\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix} + μ\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

=> $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}=\begin{bmatrix}2λ & 3λ\\λ & 2λ\end{bmatrix} + \begin{bmatrix}μ & 0\\0 & μ\end{bmatrix}$

=> $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}=\begin{bmatrix}2λ+μ & 3λ+0\\λ+0 & 2λ+μ\end{bmatrix}$

=> $\begin{bmatrix}7 & 12\\4 & 7\end{bmatrix}=\begin{bmatrix}2λ+μ & 3λ\\λ & 2λ+μ\end{bmatrix}$

Al comparar ambos lados, obtenemos,

=> 2λ + μ = 7 y λ = 4

=> 2(4) + μ = 7

=> μ = 7 – 8

=> μ = –1

Por tanto, el valor de λ es 4 y μ es –1.

Pregunta 39. Encuentra el valor de x para el cual el producto de arrays $\begin{bmatrix}2 & 0 & 7\\0 & 1 & 0\\1 & -2 & 1\end{bmatrix}\begin{bmatrix}-x & 14x & 7x\\0 & 1 & 0\\x & -4x & -2x\end{bmatrix}$ es igual a una array identidad.

Solución:

Tenemos,

=> $\begin{bmatrix}2 & 0 & 7\\0 & 1 & 0\\1 & -2 & 1\end{bmatrix}\begin{bmatrix}-x & 14x & 7x\\0 & 1 & 0\\x & -4x & -2x\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}$

=> $\begin{bmatrix}-2x+0+7x & 28x+0-28x & 14x+0-14x\\0+0+0 & 0+1-0 & 0+0-0\\-x-0+x & 14x-2-4x & 7x-0-2x\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}$

=> $\begin{bmatrix}5x & 0 & 0\\0 & 1 & 0\\0 & 10x-2 & 5x\end{bmatrix}=\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}$

Al comparar ambos lados, obtenemos,

=> 5x = 1

=> x = 1/5

Por lo tanto, el valor de x es 1/5.

Pregunta 40. Resuelve las siguientes ecuaciones matriciales:

(i)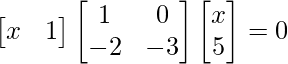 $\begin{bmatrix}x & 1\end{bmatrix}\begin{bmatrix}1 & 0\\-2 & -3\end{bmatrix}\begin{bmatrix}x \\5\end{bmatrix}=0$

Solución:

Tenemos,

=> $\begin{bmatrix}x & 1\end{bmatrix}\begin{bmatrix}1 & 0\\-2 & -3\end{bmatrix}\begin{bmatrix}x \\5\end{bmatrix}=0$

=> $\begin{bmatrix}x-2 & 0-3\end{bmatrix}\begin{bmatrix}x \\5\end{bmatrix}=0$

=> $\begin{bmatrix}x-2 & -3\end{bmatrix}\begin{bmatrix}x \\5\end{bmatrix}=0$

=> $\begin{bmatrix}x^2-2x-15\end{bmatrix}=0$

=> x2 – ^2x – 15 = 0

=> x ² – 5x + 3x – 15 = 0

=> x (x – 5) + 3 (x – 5) = 0

=> (x – 5) (x + 3) = 0

=> x = 5 o –3

Por lo tanto, el valor de x es 5 o –3.

(ii) $\begin{bmatrix}1 & 2 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 0\\2 & 0 & 1\\1&0&2\end{bmatrix}\begin{bmatrix}0 \\2\\x\end{bmatrix}=0$

Solución:

Tenemos,

=> $\begin{bmatrix}1 & 2 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 0\\2 & 0 & 1\\1&0&2\end{bmatrix}\begin{bmatrix}0 \\2\\x\end{bmatrix}=0$

=> $\begin{bmatrix}1+4+1 & 2+0+0 & 0+2+2\end{bmatrix}\begin{bmatrix}0 \\2\\x\end{bmatrix}=0$

=> $\begin{bmatrix}6 & 2 & 4\end{bmatrix}\begin{bmatrix}0 \\2\\x\end{bmatrix}=0$

=> $\begin{bmatrix}0+4+4x\end{bmatrix}=0$

=> 4 + 4x = 0

=> 4x = –4

=> x = –1

Por lo tanto, el valor de x es –1.

(iii)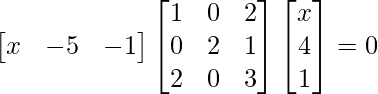 $\begin{bmatrix}x & -5 & -1\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}\begin{bmatrix}x \\4\\1\end{bmatrix}=0$

Solución:

Tenemos,

=> $\begin{bmatrix}x & -5 & -1\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}\begin{bmatrix}x \\4\\1\end{bmatrix}=0$

=> $\begin{bmatrix}x-0-2 & 0-10-0 & 2x-5-3\end{bmatrix}\begin{bmatrix}x \\4\\1\end{bmatrix}=0$

=> $\begin{bmatrix}x-2 & -10 & 2x-8\end{bmatrix}\begin{bmatrix}x \\4\\1\end{bmatrix}=0$

=> $\begin{bmatrix}x^2-2x-40+2x-8\end{bmatrix}=0$

=> x2 – 48 = ⁰

=>x2 ⁼ 48

=> x = ±4√3

Por lo tanto, el valor de x es ±4√3.

(iv)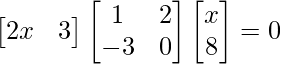 $\begin{bmatrix}2x & 3\end{bmatrix}\begin{bmatrix}1 & 2\\-3 & 0\end{bmatrix}\begin{bmatrix}x\\8 \end{bmatrix}=0$

Solución:

Tenemos,

=> $\begin{bmatrix}2x & 3\end{bmatrix}\begin{bmatrix}1 & 2\\-3 & 0\end{bmatrix}\begin{bmatrix}x\\8 \end{bmatrix}=0$

=> $\begin{bmatrix}2x-9 & 4x\end{bmatrix}\begin{bmatrix}x\\8 \end{bmatrix}=0$

=> $\begin{bmatrix}x(2x-9)+32x\end{bmatrix}=0$

=> $\begin{bmatrix}2x^2-9x+32x\end{bmatrix}=0$

=> 2×2 + 23x = ⁰

=> x (2x + 23) = 0

=> x = 0 o x = –23/2

Por lo tanto, el valor de x es 0 o –23/2.

Pregunta 41. Si A = 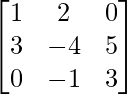$\begin{bmatrix}1 & 2 & 0\\3 & -4 & 5\\0&-1&3\end{bmatrix}$ , calcule A ² – 4A + 3I ₃ .

Solución:

Tenemos,

un = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$

un ² = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$

= $\begin{bmatrix}1+6+0 & 2-8-0 & 0+10+0\\3-12+0 & 6+16-5 & 0-20+15\\0-3+0&0+4-3&0-5+9\end{bmatrix}$

= $\begin{bmatrix}7 & -6 & 10\\-9 & 17 & -5\\-3&1&4\end{bmatrix}$

Entonces, A ² – 4A + 3I ₃ = $\begin{bmatrix}7 & -6 & 10\\-9 & 17 & -5\\-3&1&4\end{bmatrix}-4\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}+3\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0&0&1\end{bmatrix}$

= $\begin{bmatrix}7 & -6 & 10\\-9 & 17 & -5\\-3&1&4\end{bmatrix}-\begin{bmatrix}4 & 0 & 8\\0 & 8 & 4\\8&0&12\end{bmatrix}+\begin{bmatrix}3 & 0 & 0\\0 & 3 & 0\\0&0&3\end{bmatrix}$

= $\begin{bmatrix}7-4+3 & -6-8+0 & 10-0+0\\-9-12+0 & 17+16+3 & -5-20+0\\-3-0+0&1+4+0&4-12+3\end{bmatrix}$

= $\begin{bmatrix}6 & -14 & 10\\-21 & 36 & -25\\-3&5&-5\end{bmatrix}$

Pregunta 42. Si f(x) = x ² – 2x, encuentre f(A), donde A = 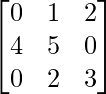$\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$ .

Solución:

Tenemos,

A = $\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$ y f(x) = x ² – 2x

un ² = $\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$

= $\begin{bmatrix}0+4+0 & 0+5+4 & 0+0+6\\0+20+0 & 4+25+0 & 8+0+0\\0+8+0&0+10+6&0+0+9\end{bmatrix}$

= $\begin{bmatrix}4 & 9 & 6\\20 & 29 & 8\\8&16&9\end{bmatrix}$

Entonces, f(A) = A ² – 2A

= $\begin{bmatrix}4 & 9 & 6\\20 & 29 & 8\\8&16&9\end{bmatrix}-2\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$

= $\begin{bmatrix}4 & 9 & 6\\20 & 29 & 8\\8&16&9\end{bmatrix}-\begin{bmatrix}0 & 2 & 4\\8 & 10 & 0\\0&4&6\end{bmatrix}$

= $\begin{bmatrix}4-0 & 9-2 & 6-4\\20-8 & 29-10 & 8-0\\8-0&16-4&9-6\end{bmatrix}$

= $\begin{bmatrix}4 & 7 & 2\\12 & 19 & 0\\8&12&3\end{bmatrix}$

Pregunta 43. Si f(x) = x ³ + 4x ² – x, encuentre f(A) donde A = 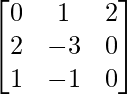$\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$ .

Solución:

Tenemos,

A = $\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$ y f(x) = x ³ + 4x ² – x

un ² = $\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$

= $\begin{bmatrix}0+2+2 & 0-3-2 & 0+0+0\\0-6+0 & 2+9-0 & 4-0+0\\0-2+0&1+3-0&2-0+0\end{bmatrix}$

= $\begin{bmatrix}4 & -5 & 0\\-6 & 11 & 4\\-2&4&2\end{bmatrix}$

UN ³ = UN ² . A

= $\begin{bmatrix}4 & -5 & 0\\-6 & 11 & 4\\-2&4&2\end{bmatrix}\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$

= $\begin{bmatrix}0-10+0 & 4+15-0 & 8-0+0\\0+22+4 & -6-33-4 & -12+0+0\\0+8+2&-2-12-2&-4+0+0\end{bmatrix}$

= $\begin{bmatrix}-10 & 19 & 8\\26 & -43 & -12\\10&-16&-4\end{bmatrix}$

Ahora, f(A) = A ³ + 4A ² – A

= $\begin{bmatrix}-10 & 19 & 8\\26 & -43 & -12\\10&-16&-4\end{bmatrix}+4\begin{bmatrix}4 & -5 & 0\\-6 & 11 & 4\\-2&4&2\end{bmatrix}-\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$

= $\begin{bmatrix}-10 & 19 & 8\\26 & -43 & -12\\10&-16&-4\end{bmatrix}+\begin{bmatrix}16 & -20 & 0\\-24 & 44 & 16\\-8&16&8\end{bmatrix}-\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$

= $\begin{bmatrix}-10+16-0 & 19-20-1 & 8+0-2\\26-24-2 & -43+44+3 & -12+16-0\\10-8-1&-16+16+1&-4+8+0\end{bmatrix}$

= $\begin{bmatrix}6 & -2 & 6\\0 & 4 & 4\\1&1&4\end{bmatrix}$

Pregunta 44. Si A = 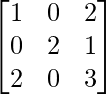$\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$ , entonces demuestre que A es una raíz del polinomio f(x) = x ³ – 6x ² + 7x +2.

Solución:

Tenemos,

A = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$ y f(x) = x ³ – 6x ² + 7x +2.

un ² = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$

= $\begin{bmatrix}1+0+4 & 0+0+0 & 2+0+6\\0+0+2 & 0+4+0 & 0+2+3\\2+0+6&0+0+0&4+0+9\end{bmatrix}$

= $\begin{bmatrix}5 & 0 & 8\\2 & 4 & 5\\8&0&13\end{bmatrix}$

UN ³ = UN ² . A

= $\begin{bmatrix}5 & 0 & 8\\2 & 4 & 5\\8&0&13\end{bmatrix}\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$

= $\begin{bmatrix}5+0+16 & 0+0+0 & 10+0+24\\2+0+10 & 0+8+0 & 4+4+15\\8+0+26&0+0+0&16+0+39\end{bmatrix}$

= $\begin{bmatrix}21 & 0 & 34\\12 & 8 & 23\\34&0&55\end{bmatrix}$

Para mostrar que A es una raíz del polinomio anterior, necesitamos probar que f(A) = 0.

Ahora, f(A) = A ³ – 6A ² + 7A + 2I

= $\begin{bmatrix}21 & 0 & 34\\12 & 8 & 23\\34&0&55\end{bmatrix}-6\begin{bmatrix}5 & 0 & 8\\2 & 4 & 5\\8&0&13\end{bmatrix}+7\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}+2\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0&0&1\end{bmatrix}$

= $\begin{bmatrix}21 & 0 & 34\\12 & 8 & 23\\34&0&55\end{bmatrix}-\begin{bmatrix}30 & 0 & 48\\12 & 24 & 30\\48&0&78\end{bmatrix}+\begin{bmatrix}7 & 0 & 14\\0 & 14 & 7\\14&0&21\end{bmatrix}+\begin{bmatrix}2 & 0 & 0\\0 & 2 & 0\\0&0&2\end{bmatrix}$

= $\begin{bmatrix}21-30+7+2 & 0-0+0+0 & 34-48+14+0\\12-12+0+0 & 8-24+14+2 & 23-30+7+0\\34-48+14+0&0-0+0+0&55-78+21+2\end{bmatrix}$

= $\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix}$

= 0

Por lo tanto probado.

Pregunta 45. Si A = 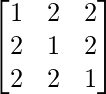$\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}$ , demuestre que A ² – 4A – 5I = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}$

un ² = $\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}$

= $\begin{bmatrix}1+4+4 & 2+2+4 & 2+4+2\\2+2+4 & 4+1+4 & 4+2+2\\2+4+2 & 4+2+2 & 4+4+1\end{bmatrix}$

= $\begin{bmatrix}9 & 8 & 8\\8 & 9 & 8\\8 & 8 & 9\end{bmatrix}$

Ahora, LHS = A ² – 4A – 5I

= $\begin{bmatrix}9 & 8 & 8\\8 & 9 & 8\\8 & 8 & 9\end{bmatrix}-4\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}-5\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}$

= $\begin{bmatrix}9 & 8 & 8\\8 & 9 & 8\\8 & 8 & 9\end{bmatrix}-\begin{bmatrix}4 & 8 & 8\\8 & 4 & 8\\8 & 8 & 4\end{bmatrix}-\begin{bmatrix}5 & 0 & 0\\0 & 5 & 0\\0 & 0 & 5\end{bmatrix}$

= $\begin{bmatrix}9-4-5 & 8-8-0 & 8-8-0\\8-8-0 & 9-4-5 & 8-8-0\\8-8-0 & 8-8-0 & 9-4-5\end{bmatrix}$

= $\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 46. Si A = 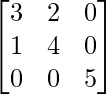$\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}$ , demuestre que A ² – 7A + 10I ₃ = 0.

Solución:

Tenemos,

un = $\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}$

un ² = $\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}$

= $\begin{bmatrix}9+2+0 & 6+8+0 & 0+0+0\\3+4+0 & 2+16+0 & 0+0+0\\0+0+0 & 0+0+0 & 0+0+25\end{bmatrix}$

= $\begin{bmatrix}11 & 14 & 0\\7 & 18 & 0\\0 & 0 & 25\end{bmatrix}$

Ahora, LHS = A ² – 7A + 10I ₃

= $\begin{bmatrix}11 & 14 & 0\\7 & 18 & 0\\0 & 0 & 25\end{bmatrix}-7\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}+10\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}$

= $\begin{bmatrix}11 & 14 & 0\\7 & 18 & 0\\0 & 0 & 25\end{bmatrix}-\begin{bmatrix}21 & 14 & 0\\7 & 28 & 0\\0 & 0 & 35\end{bmatrix}+\begin{bmatrix}10 & 0 & 0\\0 & 10 & 0\\0 & 0 & 10\end{bmatrix}$

= $\begin{bmatrix}11-21+10 & 14-14+0 & 0-0+0\\7-7+0 & 18-28+10 & 0-0+0\\0-0+0 & 0-0+0 & 25-35+10\end{bmatrix}$

= $\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix}$

= 0

= lado derecho

Por lo tanto probado.

Pregunta 47. Sin utilizar el concepto de inversa de una array, encuentre la array 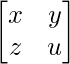$\begin{bmatrix}x & y\\z & u\end{bmatrix}$ tal que,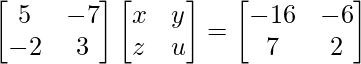 $\begin{bmatrix}5 & -7\\-2 & 3\end{bmatrix} \begin{bmatrix}x & y\\z & u\end{bmatrix} =\begin{bmatrix}-16 & -6\\7 & 2\end{bmatrix}$

Solución:

Tenemos,

=> $\begin{bmatrix}5 & -7\\-2 & 3\end{bmatrix} \begin{bmatrix}x & y\\z & u\end{bmatrix} =\begin{bmatrix}-16 & -6\\7 & 2\end{bmatrix}$

=> $\begin{bmatrix}5x-7z & 5y-7u\\-2x+3z & -2y+3u\end{bmatrix}=\begin{bmatrix}-16 & -6\\7 & 2\end{bmatrix}$

Al comparar ambos lados, obtenemos,

5x – 7z = –16

5y – 7u = –6

–2x + 3z = 7

–2y + 3u = 2

Al resolver las ecuaciones anteriores, obtenemos

=> x = 1, y = –4, z = 3 yu = –2.

Entonces, obtenemos $\begin{bmatrix}x & y\\z & u\end{bmatrix} =\begin{bmatrix}1 & -4\\3 & -2\end{bmatrix}$ .

Pregunta 48. Encuentra la array A tal que

(i)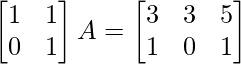 $\begin{bmatrix}1 & 1\\0 & 1\end{bmatrix}A=\begin{bmatrix}3 & 3 & 5\\1 & 0 & 1\end{bmatrix}$

Solución:

Sea A = $\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}$

La ecuación dada es,

=> $\begin{bmatrix}1 & 1\\0 & 1\end{bmatrix}A=\begin{bmatrix}3 & 3 & 5\\1 & 0 & 1\end{bmatrix}$

=> $\begin{bmatrix}1 & 1\\0 & 1\end{bmatrix}\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}=\begin{bmatrix}3 & 3 & 5\\1 & 0 & 1\end{bmatrix}$

=> $\begin{bmatrix}x+a & y+b & z+c\\a+0 & b+0 & c+0\end{bmatrix}=\begin{bmatrix}3 & 3 & 5\\1 & 0 & 1\end{bmatrix}$

=> $\begin{bmatrix}x+a & y+b & z+c\\a & b & c\end{bmatrix}=\begin{bmatrix}3 & 3 & 5\\1 & 0 & 1\end{bmatrix}$

Al comparar ambos lados, obtenemos a = 1, b = 0 y c = 1.

Y x + 1 = 3 => x = 2

Además, y = 3 y

z + 1 = 5 => z = 4

Entonces, tenemos A = $\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}=\begin{bmatrix}2 & 3 & 4\\1 & 0 & 1\end{bmatrix}$

(ii) $A\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}7 & -8 & -9\\2 & 4 & 6\end{bmatrix}$

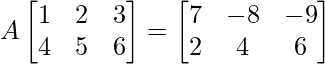
Solución:

Sea A = $\begin{bmatrix}w & x\\y & z\end{bmatrix}$

La ecuación dada es,

=> $A\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}7 & -8 & -9\\2 & 4 & 6\end{bmatrix}$

=> $\begin{bmatrix}w & x\\y & z\end{bmatrix}\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}7 & -8 & -9\\2 & 4 & 6\end{bmatrix}$

=> $\begin{bmatrix}w+4x & 2w+5x & 3w+6x\\y+4z & 2y+5z & 3y+6z\end{bmatrix}=\begin{bmatrix}7 & -8 & -9\\2 & 4 & 6\end{bmatrix}$

Al comparar ambos lados, obtenemos,

w + 4x = 7

2w + 5x = –6

y + 4z = 2

2y + 5z = 4

Al resolver las ecuaciones anteriores, obtenemos

=> x = –2, y = 2, w = 1 y z = 0.

Entonces, obtenemos A = $\begin{bmatrix}w & x\\y & z\end{bmatrix}=\begin{bmatrix}1 & -2\\2 & 0\end{bmatrix}$

(iii) $\begin{bmatrix}4\\1\\3\end{bmatrix}A=\begin{bmatrix}-4 & 8 & 4\\-1 & 2 & 1\\-3 & 6 & 3\end{bmatrix}$

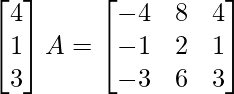
Solución:

Sea A = $\begin{bmatrix}x & y & z\end{bmatrix}$

La ecuación dada es,

=> $\begin{bmatrix}4\\1\\3\end{bmatrix}A=\begin{bmatrix}-4 & 8 & 4\\-1 & 2 & 1\\-3 & 6 & 3\end{bmatrix}$

=> $\begin{bmatrix}4\\1\\3\end{bmatrix}\begin{bmatrix}x & y & z\end{bmatrix}=\begin{bmatrix}-4 & 8 & 4\\-1 & 2 & 1\\-3 & 6 & 3\end{bmatrix}$

=> $\begin{bmatrix}4x & 4y & 4z\\x & y & z\\3x & 3y & 3z\end{bmatrix}=\begin{bmatrix}-4 & 8 & 4\\-1 & 2 & 1\\-3 & 6 & 3\end{bmatrix}$

Al comparar ambos lados, obtenemos,

=> 4x = – 4, 4y = 8 y 4z = 4.

=> x = –1, y = 2 y z = 1.

Entonces, obtenemos A = $\begin{bmatrix}-1 & 2 & 1\end{bmatrix}$

(iv) $A=\begin{bmatrix}2 & 1 & 3\end{bmatrix}\begin{bmatrix}-1 & 0 & -1\\-1 & 1 & 0\\0 & 1 &1\end{bmatrix}\begin{bmatrix}1\\0\\-1\end{bmatrix}$

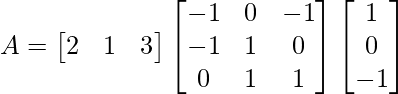
Solución:

Tenemos,

$A=\begin{bmatrix}2 & 1 & 3\end{bmatrix}\begin{bmatrix}-1 & 0 & -1\\-1 & 1 & 0\\0 & 1 &1\end{bmatrix}\begin{bmatrix}1\\0\\-1\end{bmatrix}$

un = $\begin{bmatrix}-2-1+0 & 0+1+3 & -2+0+3\end{bmatrix}\begin{bmatrix}1\\0\\-1\end{bmatrix}$

un = $\begin{bmatrix}-3 & 4 & 1\end{bmatrix}\begin{bmatrix}1\\0\\-1\end{bmatrix}$

un = $\begin{bmatrix}-3+0-1\end{bmatrix}$

un = $\begin{bmatrix}-4\end{bmatrix}$

(v) $\begin{bmatrix}2 & -1\\1 & 0\\-3 & -4\end{bmatrix}A=\begin{bmatrix}-1 & -8 & -10\\1 & -2 & -5\\9 & 22 & 15\end{bmatrix}$

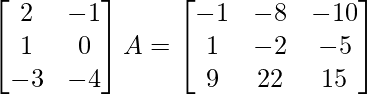
Solución:

Sea A = $\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}$

La ecuación dada es,

=> $\begin{bmatrix}2 & -1\\1 & 0\\-3 & -4\end{bmatrix}A=\begin{bmatrix}-1 & -8 & -10\\1 & -2 & -5\\9 & 22 & 15\end{bmatrix}$

=> $\begin{bmatrix}2 & -1\\1 & 0\\-3 & -4\end{bmatrix}\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}=\begin{bmatrix}-1 & -8 & -10\\1 & -2 & -5\\9 & 22 & 15\end{bmatrix}$

=> $\begin{bmatrix}2x-a & 2y-b & 2z-c\\x & y & z\\-3x+4a & -3y+4b & -3z+4c\end{bmatrix}=\begin{bmatrix}-1 & -8 & -10\\1 & -2 & -5\\9 & 22 & 15\end{bmatrix}$

Al comparar ambos lados, obtenemos,

=> x = 1, y = –2 y z = –5

Y también tenemos,

2x – a = –1

2y – b = –8

2z – c = –10

Al resolver esto, obtenemos,

=> a = 3, b = 4 y c = 0.

Entonces, obtenemos A = $\begin{bmatrix}x & y & z\\a & b & c\end{bmatrix}=\begin{bmatrix}1 & -2 & -5\\3 & 4 & 0\end{bmatrix}$

(vi) $A\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}-7 & -8 & -9\\2 & 4 & 6\\11 & 10 & 9\end{bmatrix}$

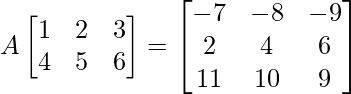
Solución:

Sea A = $\begin{bmatrix}x & a\\y & b\\z & c\end{bmatrix}$

La ecuación dada es,

=> $A\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}-7 & -8 & -9\\2 & 4 & 6\\11 & 10 & 9\end{bmatrix}$

=> $\begin{bmatrix}x & a\\y & b\\z & c\end{bmatrix}\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}=\begin{bmatrix}-7 & -8 & -9\\2 & 4 & 6\\11 & 10 & 9\end{bmatrix}$

=> $\begin{bmatrix}x+4a & 2x+5a & 3x+6a\\y+4b & 2y+5b & 3y+6b\\z+4c & 2z+5c & 3z+6c\end{bmatrix}=\begin{bmatrix}-7 & -8 & -9\\2 & 4 & 6\\11 & 10 & 9\end{bmatrix}$

Al comparar ambos lados, obtenemos

x + 4a = –7 y 2x + 5a = –8

=> x = 1 y a = –2

y + 4b = 2 y 2y + 5b = 4

=> b = 0 y y = 2

z + 4c = 11 y 2z + 5c = 10

=> c = 4 y z = –5

Entonces, obtenemos A = $\begin{bmatrix}1 & -2\\2 & 0\\-5 & 4\end{bmatrix}$

Pregunta 49. Encuentre una array A de 2 × 2 tal que 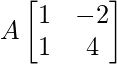$A\begin{barray}1 y -2\\1 y 4\end{barray}$ = 6I ₂ .

Solución:

Sea A = $\begin{bmatrix}w & x\\y & z\end{bmatrix}$

La ecuación dada es,

=> $A\begin{barray}1 y -2\\1 y 4\end{barray}$ = 6I

=> $\begin{bmatrix}w & x\\y & z\end{bmatrix}\begin{bmatrix}1 & -2\\1 & 4\end{bmatrix}=6\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

=> $\begin{bmatrix}w & x\\y & z\end{bmatrix}\begin{bmatrix}1 & -2\\1 & 4\end{bmatrix}=\begin{bmatrix}6 & 0\\0 & 6\end{bmatrix}$

=> $\begin{bmatrix}w+x & -2w+4x\\y+z & -2y+4z\end{bmatrix}=\begin{bmatrix}6 & 0\\0 & 6\end{bmatrix}$

Al comparar ambos lados, obtenemos

w + x = 6 y –2w + 4x = 0

=> w = 4 y x = 2

y + z = 0 y –2y + 4z = 6

=> y = –1 y z = 1

Entonces, obtenemos A = $\begin{bmatrix}w & x\\y & z\end{bmatrix}=\begin{bmatrix}4 & 2\\-1 & 1\end{bmatrix}$

Pregunta 50. Si A = $\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}$ , encuentra A ¹⁶ .

Solución:

Tenemos,

un = $\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}$

un ² = $\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}$

= $\begin{bmatrix}0+0 & 0+0\\0+0 & 0+0\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

UN ¹⁶ = UN ² UN ² UN ² UN ²

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

= $\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}$

Pregunta 51. Si A = 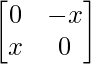$\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}$ , B = $\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}$ y x ² = –1, entonces demuestre que (A + B) ² = A ² + B ² .

Solución:

Tenemos,

A = $\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}$ , B = $\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}$ y x ² = –1

LHS = (A + B) ²

= $\left(\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}+\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}\right)^2$

= $\left(\begin{bmatrix}0+0 & -x+1\\x+1 & 0+0\end{bmatrix}\right)^2$

= $\left(\begin{bmatrix}0 & -x+1\\x+1 & 0\end{bmatrix}\right)^2$

= $\begin{bmatrix}0 & -x+1\\x+1 & 0\end{bmatrix}\begin{bmatrix}0 & -x+1\\x+1 & 0\end{bmatrix}$

= $\begin{bmatrix}0+(1-x)(1+x)& 0+0\\0+0 & (x+1)(1-x)+0\end{bmatrix}$

= $\begin{bmatrix}1-x^2 & 0\\0 & 1-x^2\end{bmatrix}$

= $\begin{bmatrix}1-(-1) & 0\\0 & 1-(-1)\end{bmatrix}$

= $\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

RHS = A ² + B ²

= $\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}+\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}$

= $\begin{bmatrix}0-x^2 & 0+0\\0+0 & -x^2+0\end{bmatrix}+\begin{bmatrix}0+1 & 0+0\\0+0 & 1+0\end{bmatrix}$

= $\begin{bmatrix}-x^2 & 0\\0 & -x^2\end{bmatrix}+\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$

= $\begin{bmatrix}1-x^2 & 0\\0 & 1-x^2\end{bmatrix}$

= $\begin{bmatrix}1-(-1) & 0\\0 & 1-(-1)\end{bmatrix}$

= $\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}$

= LHS

Por lo tanto probado.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 5 Álgebra de Arrays – Ejercicio 5.3 | conjunto 2

Pregunta 26. Si $\begin{bmatrix}1 & -1 & x\end{bmatrix}\begin{bmatrix}0 & 1 & -1\\2 & 1 & 3\\1 & 1 & 1\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}$ = 0, encuentra x.

Pregunta 27. Si A = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces demuestre que A ² – A + 2I = 0.

Pregunta 28. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces encuentra λ tal que A ² = 5A + λI.

Pregunta 29. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , demuestre que A ² – 5A + 7I ₂ = 0.

Pregunta 30. Si A = $\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}$ , demuestre que A ² – 2A + 3I ₂ = 0.

Pregunta 31. Demuestra que la array A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ satisface la ecuación A ³ – 4A ² + A = 0.

Pregunta 32. Demostrar que la array A = $\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}$ es raíz de la ecuación A ² – 12A – I = 0

Pregunta 33. Si A = $\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}$ encuentra A ² – 5A – 14I.

Pregunta 34. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , encuentra A ² – 5A + 7I = 0. Usa esto para encontrar A ⁴ .

Pregunta 35. Si A = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ , encuentra k tal que A ² = kA – 2I ₂ .

Pregunta 36. Si A = $\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}$ , encuentra k tal que A ² – 8A + kI = 0.

Pregunta 37. Si A = $\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}$ y f(x) = x ² – 2x – 3, demuestre que f(A) = 0.

Pregunta 38. Si A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , encuentre λ, μ para que A ² = λA + μI.

Pregunta 39. Encuentra el valor de x para el cual el producto de arrays $\begin{bmatrix}2 & 0 & 7\\0 & 1 & 0\\1 & -2 & 1\end{bmatrix}\begin{bmatrix}-x & 14x & 7x\\0 & 1 & 0\\x & -4x & -2x\end{bmatrix}$ es igual a una array identidad.

Pregunta 40. Resuelve las siguientes ecuaciones matriciales:

Pregunta 41. Si A = $\begin{bmatrix}1 & 2 & 0\\3 & -4 & 5\\0&-1&3\end{bmatrix}$ , calcule A ² – 4A + 3I ₃ .

Pregunta 42. Si f(x) = x ² – 2x, encuentre f(A), donde A = $\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$ .

Pregunta 43. Si f(x) = x ³ + 4x ² – x, encuentre f(A) donde A = $\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$ .

Pregunta 44. Si A = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$ , entonces demuestre que A es una raíz del polinomio f(x) = x ³ – 6x ² + 7x +2.

Pregunta 45. Si A = $\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}$ , demuestre que A ² – 4A – 5I = 0.

Pregunta 46. Si A = $\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}$ , demuestre que A ² – 7A + 10I ₃ = 0.

Pregunta 47. Sin utilizar el concepto de inversa de una array, encuentre la array $\begin{bmatrix}x & y\\z & u\end{bmatrix}$ tal que, $\begin{bmatrix}5 & -7\\-2 & 3\end{bmatrix} \begin{bmatrix}x & y\\z & u\end{bmatrix} =\begin{bmatrix}-16 & -6\\7 & 2\end{bmatrix}$

Pregunta 48. Encuentra la array A tal que

Pregunta 49. Encuentre una array A de 2 × 2 tal que $A\begin{barray}1 y -2\\1 y 4\end{barray}$ = 6I ₂ .

Pregunta 50. Si A = $\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}$ , encuentra A ¹⁶ .

Pregunta 51. Si A = $\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}$ , B = $\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}$ y x ² = –1, entonces demuestre que (A + B) ² = A ² + B ² .

Deja una respuesta Cancelar la respuesta

Pregunta 26. Si = 0, encuentra x.

Pregunta 27. Si A = e I = , entonces demuestre que A 2 – A + 2I = 0.

Pregunta 28. Si A = e I = , entonces encuentra λ tal que A 2 = 5A + λI.

Pregunta 29. Si A = , demuestre que A 2 – 5A + 7I 2 = 0.

Pregunta 30. Si A = , demuestre que A 2 – 2A + 3I 2 = 0.

Pregunta 31. Demuestra que la array A = satisface la ecuación A 3 – 4A 2 + A = 0.

Pregunta 32. Demostrar que la array A = es raíz de la ecuación A 2 – 12A – I = 0

Pregunta 33. Si A = encuentra A 2 – 5A – 14I.

Pregunta 34. Si A = , encuentra A 2 – 5A + 7I = 0. Usa esto para encontrar A 4 .

Pregunta 35. Si A = , encuentra k tal que A 2 = kA – 2I 2 .

Pregunta 36. Si A = , encuentra k tal que A 2 – 8A + kI = 0.

Pregunta 37. Si A = y f(x) = x 2 – 2x – 3, demuestre que f(A) = 0.

Pregunta 38. Si A = e I = , encuentre λ, μ para que A 2 = λA + μI.

Pregunta 39. Encuentra el valor de x para el cual el producto de arrays es igual a una array identidad.

Pregunta 40. Resuelve las siguientes ecuaciones matriciales:

Pregunta 41. Si A = , calcule A 2 – 4A + 3I 3 .

Pregunta 42. Si f(x) = x 2 – 2x, encuentre f(A), donde A = .

Pregunta 43. Si f(x) = x 3 + 4x 2 – x, encuentre f(A) donde A = .

Pregunta 44. Si A = , entonces demuestre que A es una raíz del polinomio f(x) = x 3 – 6x 2 + 7x +2.

Pregunta 45. Si A = , demuestre que A 2 – 4A – 5I = 0.

Pregunta 46. Si A = , demuestre que A 2 – 7A + 10I 3 = 0.

Pregunta 47. Sin utilizar el concepto de inversa de una array, encuentre la array tal que,

Pregunta 48. Encuentra la array A tal que

Pregunta 49. Encuentre una array A de 2 × 2 tal que = 6I 2 .

Pregunta 50. Si A = , encuentra A 16 .

Pregunta 51. Si A = , B = y x 2 = –1, entonces demuestre que (A + B) 2 = A 2 + B 2 .

Deja una respuesta Cancelar la respuesta

Pregunta 26. Si $\begin{bmatrix}1 & -1 & x\end{bmatrix}\begin{bmatrix}0 & 1 & -1\\2 & 1 & 3\\1 & 1 & 1\end{bmatrix}\begin{bmatrix}0\\1\\1\end{bmatrix}$ = 0, encuentra x.

Pregunta 27. Si A = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces demuestre que A ² – A + 2I = 0.

Pregunta 28. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , entonces encuentra λ tal que A ² = 5A + λI.

Pregunta 29. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , demuestre que A ² – 5A + 7I ₂ = 0.

Pregunta 30. Si A = $\begin{bmatrix}2 & 3\\-1 & 0\end{bmatrix}$ , demuestre que A ² – 2A + 3I ₂ = 0.

Pregunta 31. Demuestra que la array A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ satisface la ecuación A ³ – 4A ² + A = 0.

Pregunta 32. Demostrar que la array A = $\begin{bmatrix}5 & 3\\12 & 7\end{bmatrix}$ es raíz de la ecuación A ² – 12A – I = 0

Pregunta 33. Si A = $\begin{bmatrix}3 & -5\\-4 & 2\end{bmatrix}$ encuentra A ² – 5A – 14I.

Pregunta 34. Si A = $\begin{bmatrix}3 & 1\\-1 & 2\end{bmatrix}$ , encuentra A ² – 5A + 7I = 0. Usa esto para encontrar A ⁴ .

Pregunta 35. Si A = $\begin{bmatrix}3 & -2\\4 & -2\end{bmatrix}$ , encuentra k tal que A ² = kA – 2I ₂ .

Pregunta 36. Si A = $\begin{bmatrix}1 & 0\\-1 & 7\end{bmatrix}$ , encuentra k tal que A ² – 8A + kI = 0.

Pregunta 37. Si A = $\begin{bmatrix}1 & 2\\2 & 1\end{bmatrix}$ y f(x) = x ² – 2x – 3, demuestre que f(A) = 0.

Pregunta 38. Si A = $\begin{bmatrix}2 & 3\\1 & 2\end{bmatrix}$ e I = $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$ , encuentre λ, μ para que A ² = λA + μI.

Pregunta 39. Encuentra el valor de x para el cual el producto de arrays $\begin{bmatrix}2 & 0 & 7\\0 & 1 & 0\\1 & -2 & 1\end{bmatrix}\begin{bmatrix}-x & 14x & 7x\\0 & 1 & 0\\x & -4x & -2x\end{bmatrix}$ es igual a una array identidad.

Pregunta 41. Si A = $\begin{bmatrix}1 & 2 & 0\\3 & -4 & 5\\0&-1&3\end{bmatrix}$ , calcule A ² – 4A + 3I ₃ .

Pregunta 42. Si f(x) = x ² – 2x, encuentre f(A), donde A = $\begin{bmatrix}0 & 1 & 2\\4 & 5 & 0\\0&2&3\end{bmatrix}$ .

Pregunta 43. Si f(x) = x ³ + 4x ² – x, encuentre f(A) donde A = $\begin{bmatrix}0 & 1 & 2\\2 & -3 & 0\\1&-1&0\end{bmatrix}$ .

Pregunta 44. Si A = $\begin{bmatrix}1 & 0 & 2\\0 & 2 & 1\\2&0&3\end{bmatrix}$ , entonces demuestre que A es una raíz del polinomio f(x) = x ³ – 6x ² + 7x +2.

Pregunta 45. Si A = $\begin{bmatrix}1 & 2 & 2\\2 & 1 & 2\\2 & 2 & 1\end{bmatrix}$ , demuestre que A ² – 4A – 5I = 0.

Pregunta 46. Si A = $\begin{bmatrix}3 & 2 & 0\\1 & 4 & 0\\0 & 0 & 5\end{bmatrix}$ , demuestre que A ² – 7A + 10I ₃ = 0.

Pregunta 47. Sin utilizar el concepto de inversa de una array, encuentre la array $\begin{bmatrix}x & y\\z & u\end{bmatrix}$ tal que, $\begin{bmatrix}5 & -7\\-2 & 3\end{bmatrix} \begin{bmatrix}x & y\\z & u\end{bmatrix} =\begin{bmatrix}-16 & -6\\7 & 2\end{bmatrix}$

Pregunta 49. Encuentre una array A de 2 × 2 tal que $A\begin{barray}1 y -2\\1 y 4\end{barray}$ = 6I ₂ .

Pregunta 50. Si A = $\begin{bmatrix}0 & 0\\4 & 0\end{bmatrix}$ , encuentra A ¹⁶ .

Pregunta 51. Si A = $\begin{bmatrix}0 & -x\\x & 0\end{bmatrix}$ , B = $\begin{bmatrix}0 & 1\\1 & 0\end{bmatrix}$ y x ² = –1, entonces demuestre que (A + B) ² = A ² + B ² .