Dados dos enteros 
y 
. La tarea es encontrar el valor máximo de x, tal que, n! % (k^x) = 0 .
Ejemplos :
Input : n = 5, k = 2 Output : 3 Explanation : Given n = 5 and k = 2. So, n! = 120. Now for different values of x: n! % 2^0 = 0, n! % 2^1 = 0, n! % 2^2 = 0, n! % 2^3 = 0, n! % 2^4 = 8, n! % 2^5 = 24, n! % 2^6 = 56, n! % 2^7 = 120. So, the answer should be 3. Input : n = 1000, x = 2 Output : 994
Enfoque :
- Primero tome la raíz cuadrada de 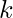y guárdela en una variable, por ejemplo,
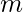. - Ejecute el ciclo desde i=2 hasta m.
- Si i = m entonces copie k en i.
- Si k es divisible por i entonces divide k por i.
- Ejecute un ciclo a n y agregue el cociente a una variable, digamos,
. - Almacene el valor mínimo de r después de cada ciclo.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to maximize the value
// of x such that n! % (k^x) = 0
#include<iostream>
#include<math.h>
using namespace std;
class GfG
{
// Function to maximize the value
// of x such that n! % (k^x) = 0
public:
int findX(int n, int k)
{
int r = n, v, u;
// Find square root of k and add 1 to it
int m = sqrt(k) + 1;
// Run the loop from 2 to m and k
// should be greater than 1
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
// optimize the value of k
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
// Minimum store
r = min(r, u / v);
}
}
return r;
}
};
// Driver Code
int main()
{
GfG g;
int n = 5;
int k = 2;
cout<<g.findX(n, k);
}
//This code is contributed by Soumik
Java
// Java program to maximize the value
// of x such that n! % (k^x) = 0
import java.util.*;
public class GfG {
// Function to maximize the value
// of x such that n! % (k^x) = 0
private static int findX(int n, int k)
{
int r = n, v, u;
// Find square root of k and add 1 to it
int m = (int)Math.sqrt(k) + 1;
// Run the loop from 2 to m and k
// should be greater than 1
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
// optimize the value of k
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
// Minimum store
r = Math.min(r, u / v);
}
}
return r;
}
// Driver Code
public static void main(String args[])
{
int n = 5;
int k = 2;
System.out.println(findX(n, k));
}
}
Python 3
# Python 3 program to maximize the value # of x such that n! % (k^x) = 0 import math # Function to maximize the value # of x such that n! % (k^x) = 0 def findX(n, k): r = n # Find square root of k # and add 1 to it m = int(math.sqrt(k)) + 1 # Run the loop from 2 to m # and k should be greater than 1 i = 2 while i <= m and k > 1 : if (i == m) : i = k # optimize the value of k u = 0 v = 0 while k % i == 0 : k //= i v += 1 if (v > 0) : t = n while (t > 0) : t //= i u += t # Minimum store r = min(r, u // v) i += 1 return r # Driver Code if __name__ == "__main__": n = 5 k = 2 print(findX(n, k)) # This code is contributed # by ChitraNayal
C#
// C# program to maximize the value
// of x such that n! % (k^x) = 0
using System;
class GfG
{
// Function to maximize the value
// of x such that n! % (k^x) = 0
public int findX(int n, int k)
{
int r = n, v, u;
// Find square root of k and add 1 to it
int m = (int)Math.Sqrt(k) + 1;
// Run the loop from 2 to m and k
// should be greater than 1
for (int i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
// optimize the value of k
for (u = v = 0; k % i == 0; v++) {
k /= i;
}
if (v > 0) {
int t = n;
while (t > 0) {
t /= i;
u += t;
}
// Minimum store
r = Math.Min(r, u / v);
}
}
return r;
}
}
// Driver Code
class geek
{
public static void Main()
{
GfG g = new GfG();
int n = 5;
int k = 2;
Console.WriteLine(g.findX(n, k));
}
}
PHP
<?php
// PHP program to maximize the value
// of x such that n! % (k^x) = 0
// Function to maximize the value
// of x such that n! % (k^x) = 0
function findX($n, $k)
{
$r = $n;
// Find square root of k and add 1 to it
$m = (int)sqrt($k) + 1;
// Run the loop from 2 to m and k
// should be greater than 1
for ($i = 2; $i <= $m && $k > 1; $i++)
{
if ($i == $m)
{
$i = $k;
}
// optimize the value of k
for ($u = $v = 0; $k % $i == 0; $v++)
{
$k = (int)($k / $i);
}
if ($v > 0)
{
$t = $n;
while ($t > 0)
{
$t = (int)($t / $i);
$u = $u + $t;
}
// Minimum store
$r = min($r, (int)($u / $v));
}
}
return $r;
}
// Driver Code
$n = 5;
$k = 2;
echo findX($n, $k);
// This code is contributed by
// Archana_kumari
?>
Javascript
<script>
// Javascript program to maximize the value
// of x such that n! % (k^x) = 0
// Function to maximize the value
// of x such that n! % (k^x) = 0
function findX(n, k)
{
let r = n;
let v = 0;
let u = 0;
// Find square root of k and add 1 to it
let m = Math.floor(Math.sqrt(k) + 1);
// Run the loop from 2 to m and k
// should be greater than 1
for (let i = 2; i <= m && k > 1; i++) {
if (i == m) {
i = k;
}
// optimize the value of k
for (let u = v = 0; k % i == 0; v++) {
k = Math.floor(k / i);
}
if (v > 0) {
let t = n;
while (t > 0) {
t = Math.floor(t / i);
u += t;
}
// Minimum store
r = Math.min(r, Math.floor(u / v));
}
}
return r;
}
// Driver Code
let n = 5;
let k = 2;
document.write(findX(n, k));
//This code is contributed by gfgking
</script>
Producción:
3
Publicación traducida automáticamente
Artículo escrito por VishalBachchas y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA