Encuentre la suma de la diferencia de máximo y mínimo sobre todos los subconjuntos posibles de tamaño K

Posted on by Rudeus Greyrat

Dada una array arr[] de N enteros y un entero K , la tarea es encontrar la suma de la diferencia entre los elementos máximo y mínimo sobre todos los subconjuntos posibles de tamaño K.

Ejemplos:

Entrada: arr[] = {1, 1, 3, 4}, K = 2
Salida: 11
Explicación:
Hay 6 subconjuntos de la array dada de tamaño K(= 2). Son {1, 1}, {1, 3}, {1, 4}, {1, 3}, {1, 4} y {3, 4}.
Los valores de máximo – mínimo para cada uno de los subconjuntos respectivamente son 0, 2, 3, 2, 3, 1 y su suma es 11.

Entrada: arr[] = {1, 1, 1}, K = 1
Salida: 0

 

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones:

  • La suma de la diferencia entre el máximo y el mínimo de todos los conjuntos es independiente entre sí, es decir, se puede calcular como la suma del máximo de todos los conjuntos de tamaño K, la suma del mínimo de todos los conjuntos de tamaño K.
  • En una array ordenada arr[] , arr[i] es el máximo de todos los conjuntos que tienen elementos de la array en el rango [0, i – 1] . Por lo tanto, el número de conjuntos de tamaño K que tienen arr[i] como elemento de array máximo se puede calcular como 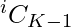 {}^{i}C_{K - 1} . De manera similar, el número de conjuntos de tamaño K que tienen arr[i] como elemento mínimo son  {}^{N - i - 1}C_{K - 1} .
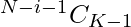  • El valor de 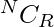 {}^{N}C_{R}  se puede calcular de manera eficiente utilizando el enfoque que se analiza en este artículo .

Usando las observaciones anteriores, el problema dado se puede resolver siguiendo los pasos a continuación:

  • Ordene la array dada arr[] en orden no decreciente.
  • Para calcular la suma del máximo de todos los conjuntos de tamaño K , cree una variable sumMax , y para cada uno, el índice i en el rango [K – 1, N – 1] , itere a través de la array arr[] y agregue  arr[i] * {}^{i}C_{K - 1}  en sumMax .
  • De manera similar, para calcular la suma del mínimo de todos los conjuntos de tamaño K , cree una variable sumMin y para cada i en el rango [0, NK], itere a través de la array arr[] y agréguela  arr[i] * {}^{N - i - 1}C_{K - 1}  a sumMin .
  • El valor de sumMax – sumMin es la respuesta requerida.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
#define int long long int
#define max 100000
#define mod 1000000007
 
int inv[max], fact[max], facinv[max];
 
// Function to precompute factorial and
// the inverse of factorial values of all
// elements in the range [1, max] to find
// the value of nCr in O(1)
void ncrPrecomputation()
{
    inv[0] = inv[1] = 1;
    fact[0] = fact[1] = 1;
    facinv[0] = facinv[1] = 1;
 
    // Loop to iterate over all i in
    // the range [2, max]
    for (int i = 2; i < max; i++) {
 
        // Calculate Inverse of i
        inv[i] = inv[mod % i]
                 * (mod - mod / i) % mod;
 
        // Calculate Factorial of i
        fact[i] = (fact[i - 1] * i) % mod;
 
        // Calculate the Inverse of
        // factorial of i
        facinv[i] = (inv[i] * facinv[i - 1]) % mod;
    }
}
 
// Function to find nCr in O(1)
int nCr(int n, int r)
{
    return ((fact[n] * facinv[r]) % mod
            * facinv[n - r])
           % mod;
}
 
// Function to find the sum of difference
// between maximum and minimum over all
// sets of arr[] having K elements
int sumMaxMin(int arr[], int N, int K)
{
    // Sort the given array
    sort(arr, arr + N);
 
    // Stores the sum of maximum of
    // all the sets
    int sumMax = 0;
 
    // Loop to iterate arr[] in the
    // range [K-1, N-1]
    for (int i = K - 1; i < N; i++) {
 
        // Add sum of sets having arr[i]
        // as the maximum element
        sumMax += (arr[i] * nCr(i, K - 1));
    }
 
    // Stores the sum of the minimum of
    // all the sets
    int sumMin = 0;
 
    // Loop to iterate arr[] in the
    // range [0, N - K]
    for (int i = 0; i <= N - K; i++) {
 
        // Add sum of sets having arr[i]
        // as the minimum element
        sumMin += (arr[i] * nCr(N - i - 1, K - 1));
    }
 
    // Return answer
    return (sumMax - sumMin);
}
 
// Driver Code
signed main()
{
    int arr[] = { 1, 1, 3, 4 };
    int K = 2;
    int N = sizeof(arr) / sizeof(arr[0]);
 
    ncrPrecomputation();
 
    cout << sumMaxMin(arr, N, K);
 
    return 0;
}

Java

// Java program for the above approach
import java.io.*;
import java.util.*;
 
class GFG {
 
    static final int max = 100000;
    static final int mod = 1000000007;
 
    static long inv[] = new long[max], fact[] = new long[max],
               facinv[] = new long[max];
 
    // Function to precompute factorial and
    // the inverse of factorial values of all
    // elements in the range [1, max] to find
    // the value of nCr in O(1)
    static void ncrPrecomputation()
    {
        inv[0] = inv[1] = 1;
        fact[0] = fact[1] = 1;
        facinv[0] = facinv[1] = 1;
 
        // Loop to iterate over all i in
        // the range [2, max]
        for (int i = 2; i < max; i++) {
 
            // Calculate Inverse of i
            inv[i] = inv[mod % i] * (mod - mod / i) % mod;
 
            // Calculate Factorial of i
            fact[i] = (fact[i - 1] * i) % mod;
 
            // Calculate the Inverse of
            // factorial of i
            facinv[i] = (inv[i] * facinv[i - 1]) % mod;
        }
    }
 
    // Function to find nCr in O(1)
    static long nCr(long n, long r)
    {
        return ((fact[(int)n] * facinv[(int)r]) % mod * facinv[(int)(n - r)])
            % mod;
    }
 
    // Function to find the sum of difference
    // between maximum and minimum over all
    // sets of arr[] having K elements
    static long sumMaxMin(long arr[], long N, long K)
    {
        // Sort the given array
        Arrays.sort(arr);
 
        // Stores the sum of maximum of
        // all the sets
        long sumMax = 0;
 
        // Loop to iterate arr[] in the
        // range [K-1, N-1]
        for (int i = (int)K - 1; i < N; i++) {
 
            // Add sum of sets having arr[i]
            // as the maximum element
            sumMax += (arr[i] * nCr(i, K - 1));
        }
 
        // Stores the sum of the minimum of
        // all the sets
        long sumMin = 0;
 
        // Loop to iterate arr[] in the
        // range [0, N - K]
        for (int i = 0; i <= N - K; i++) {
 
            // Add sum of sets having arr[i]
            // as the minimum element
            sumMin += (arr[i] * nCr(N - i - 1, K - 1));
        }
 
        // Return answer
        return (sumMax - sumMin);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        long arr[] = { 1, 1, 3, 4 };
        long K = 2;
        long N = arr.length;
 
        ncrPrecomputation();
 
        System.out.println(sumMaxMin(arr, N, K));
    }
}
 
// This code is contributed by Dharanendra L V.

C#

// C# program for the above approach
using System;
public class GFG
{
 
    static readonly int max = 100000;
    static readonly int mod = 1000000007;
 
    static long []inv = new long[max];
    static long []fact = new long[max];
    static long []facinv = new long[max];
 
    // Function to precompute factorial and
    // the inverse of factorial values of all
    // elements in the range [1, max] to find
    // the value of nCr in O(1)
    static void ncrPrecomputation()
    {
        inv[0] = inv[1] = 1;
        fact[0] = fact[1] = 1;
        facinv[0] = facinv[1] = 1;
 
        // Loop to iterate over all i in
        // the range [2, max]
        for (int i = 2; i < max; i++) {
 
            // Calculate Inverse of i
            inv[i] = inv[mod % i] * (mod - mod / i) % mod;
 
            // Calculate Factorial of i
            fact[i] = (fact[i - 1] * i) % mod;
 
            // Calculate the Inverse of
            // factorial of i
            facinv[i] = (inv[i] * facinv[i - 1]) % mod;
        }
    }
 
    // Function to find nCr in O(1)
    static long nCr(long n, long r)
    {
        return ((fact[(int)n] * facinv[(int)r]) % mod * facinv[(int)(n - r)])
            % mod;
    }
 
    // Function to find the sum of difference
    // between maximum and minimum over all
    // sets of []arr having K elements
    static long sumMaxMin(long []arr, long N, long K)
    {
        // Sort the given array
        Array.Sort(arr);
 
        // Stores the sum of maximum of
        // all the sets
        long sumMax = 0;
 
        // Loop to iterate []arr in the
        // range [K-1, N-1]
        for (int i = (int)K - 1; i < N; i++) {
 
            // Add sum of sets having arr[i]
            // as the maximum element
            sumMax += (arr[i] * nCr(i, K - 1));
        }
 
        // Stores the sum of the minimum of
        // all the sets
        long sumMin = 0;
 
        // Loop to iterate []arr in the
        // range [0, N - K]
        for (int i = 0; i <= N - K; i++) {
 
            // Add sum of sets having arr[i]
            // as the minimum element
            sumMin += (arr[i] * nCr(N - i - 1, K - 1));
        }
 
        // Return answer
        return (sumMax - sumMin);
    }
 
    // Driver Code
    public static void Main(String[] args)
    {
        long []arr = { 1, 1, 3, 4 };
        long K = 2;
        long N = arr.Length;
 
        ncrPrecomputation();
 
        Console.WriteLine(sumMaxMin(arr, N, K));
    }
}
 
// This code is contributed by 29AjayKumar

Python3

# Python 3 program for the above approach
 
max1 = 100000
mod = 1000000007
 
inv = [0 for i in range(max1)]
fact = [0 for i in range(max1)]
facinv = [0 for i in range(max1)]
 
# Function to precompute factorial and
# the inverse of factorial values of all
# elements in the range [1, max] to find
# the value of nCr in O(1)
def ncrPrecomputation():
    inv[0] = inv[1] = 1
    fact[0] = fact[1] = 1
    facinv[0] = facinv[1] = 1
 
    # Loop to iterate over all i in
    # the range [2, max]
    for i in range(2,max1,1):
        # Calculate Inverse of i
        inv[i] = inv[mod % i] * (mod - mod // i) % mod
 
        # Calculate Factorial of i
        fact[i] = (fact[i - 1] * i) % mod
 
        # Calculate the Inverse of
        # factorial of i
        facinv[i] = (inv[i] * facinv[i - 1]) % mod
 
# Function to find nCr in O(1)
def nCr(n,r):
    return ((fact[n] * facinv[r]) % mod * facinv[n - r]) % mod
 
# Function to find the sum of difference
# between maximum and minimum over all
# sets of arr[] having K elements
def sumMaxMin(arr, N, K):
    # Sort the given array
    arr.sort()
 
    # Stores the sum of maximum of
    # all the sets
    sumMax = 0
 
    # Loop to iterate arr[] in the
    # range [K-1, N-1]
    for i in range(K - 1,N,1):
        # Add sum of sets having arr[i]
        # as the maximum element
        sumMax += (arr[i] * nCr(i, K - 1))
 
    # Stores the sum of the minimum of
    # all the sets
    sumMin = 0
 
    # Loop to iterate arr[] in the
    # range [0, N - K]
    for i in range(N - K+1):
        # Add sum of sets having arr[i]
        # as the minimum element
        sumMin += (arr[i] * nCr(N - i - 1, K - 1))
 
    # Return answer
    return (sumMax - sumMin)
 
# Driver Code
if __name__ == '__main__':
    arr = [1, 1, 3, 4]
    K = 2
    N = len(arr)
    ncrPrecomputation()
    print(sumMaxMin(arr, N, K))
     
    # This code is contributed by SURENDRA_GANGWAR

Javascript

<script>
// JaVASCRIPT program for the above approach
 
let max = 100000;
let mod = 1000000007;
 
let inv = new Array(max).fill(0),
  fact = new Array(max).fill(0),
  facinv = new Array(max).fill(0);
 
// Function to precompute factorial and
// the inverse of factorial values of all
// elements in the range [1, max] to find
// the value of nCr in O(1)
function ncrPrecomputation() {
  inv[0] = inv[1] = 1;
  fact[0] = fact[1] = 1;
  facinv[0] = facinv[1] = 1;
 
  // Loop to iterate over all i in
  // the range [2, max]
  for (let i = 2; i < max; i++) {
    // Calculate Inverse of i
    inv[i] = (inv[mod % i] * Math.ceil(mod - mod / i)) % mod;
 
    // Calculate Factorial of i
    fact[i] = (fact[i - 1] * i) % mod;
 
    // Calculate the Inverse of
    // factorial of i
    facinv[i] = (inv[i] * facinv[i - 1]) % mod;
  }
}
 
// Function to find nCr in O(1)
function nCr(n, r) {
  return (((fact[n] * facinv[r]) % mod) * facinv[n - r]) % mod;
}
 
// Function to find the sum of difference
// between maximum and minimum over all
// sets of arr[] having K elements
function sumMaxMin(arr, N, K) {
  // Sort the given array
  arr.sort((a, b) => a - b);
 
  // Stores the sum of maximum of
  // all the sets
  let sumMax = 0;
 
  // Loop to iterate arr[] in the
  // range [K-1, N-1]
  for (let i = K - 1; i < N; i++) {
    // Add sum of sets having arr[i]
    // as the maximum element
    sumMax += arr[i] * nCr(i, K - 1);
  }
 
  // Stores the sum of the minimum of
  // all the sets
  let sumMin = 0;
 
  // Loop to iterate arr[] in the
  // range [0, N - K]
  for (let i = 0; i <= N - K; i++) {
    // Add sum of sets having arr[i]
    // as the minimum element
    sumMin += arr[i] * nCr(N - i - 1, K - 1);
  }
 
  // Return answer
  return sumMax - sumMin;
}
 
// Driver Code
 
let arr = [1, 1, 3, 4];
let K = 2;
let N = arr.length;
 
ncrPrecomputation();
 
document.write(sumMaxMin(arr, N, K));
 
// This code is contributed by saurabh_jaiswal.
</script>
Producción: 

11

 

Complejidad de tiempo: O(N*log N)
Espacio auxiliar: O(N)

Publicación traducida automáticamente

Artículo escrito por kartikmodi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *