Tipos de función de activación en ANN

La red neuronal biológica se ha modelado en forma de Redes Neuronales Artificiales con neuronas artificiales que simulan la función de una neurona biológica. La neurona artificial se representa en la siguiente imagen:

Cada neurona consta de tres componentes principales:

Un conjunto de sinapsis ‘i’ que tienen peso w _i . Una señal x _i forma la entrada a la i-ésima sinapsis que tiene peso w _i . El valor de cualquier peso puede ser positivo o negativo. Un peso positivo tiene un efecto extraordinario, mientras que un peso negativo tiene un efecto inhibitorio sobre la salida de la unión de suma.
Una unión de suma para las señales de entrada es ponderada por el peso sináptico respectivo. Debido a que es un combinador o sumador lineal de las señales de entrada ponderadas, la salida de la unión de suma se puede expresar de la siguiente manera: $y_{sum}=\sum_{i=1}^{n}w_ix_i$
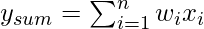
Una función de activación de umbral (o simplemente la función de activación, también conocida como función de aplastamiento ) da como resultado una señal de salida solo cuando una señal de entrada que excede un valor de umbral específico llega como entrada. Es similar en comportamiento a la neurona biológica que transmite la señal solo cuando la señal de entrada total alcanza el umbral de activación.

Hay diferentes tipos de funciones de activación. Las funciones de activación más utilizadas se enumeran a continuación:

A. Función de identidad: la función de identidad se utiliza como función de activación para la capa de entrada. es una función lineal que tiene la forma

$y_{out}=f(x)=x, \forall x$

Como es obvio, la salida sigue siendo la misma que la entrada.

B. Función de umbral/paso: es una función de activación de uso común. Como se muestra en el diagrama, da 1 ya que la salida de la entrada es 0 o positiva. Si la entrada es negativa, da 0 como salida . Expresándolo matemáticamente,

$y_{out}=f(y_{sum})=\bigg\{\begin{matrix} 1, x \geq 0 \\ 0, x < 0 \end{matrix}$

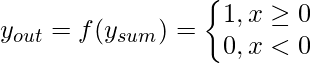
La función de umbral es casi como la función de paso, con la única diferencia de que $\theta$ se utiliza como valor de umbral en lugar de . Expresando matemáticamente,

$y_{out}=f(y_{sum})=\bigg\{\begin{matrix} 1, x \geq \theta \\ 0, x < \theta \end{matrix}$

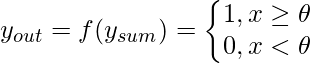
C. Función ReLU (Unidad lineal rectificada): es la función de activación más utilizada en las áreas de redes neuronales convolucionales y aprendizaje profundo. es de la forma:

$f(x)=\bigg\{\begin{matrix} x, x \geq 0\\ 0, x < 0 \end{matrix}$

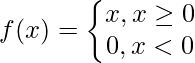
Esto significa que f(x) es cero cuando x es menor que cero y f(x) es igual ax cuando x es mayor o igual a cero. Esta función es diferenciable , excepto en un solo punto x = 0. En ese sentido, la derivada de ReLU es en realidad una subderivada.

D. Función sigmoidea: es, con diferencia, la función de activación más utilizada en las redes neuronales. La necesidad de una función sigmoidea surge del hecho de que muchos algoritmos de aprendizaje requieren que la función de activación sea diferenciable y, por lo tanto, continua. Hay dos tipos de función sigmoidea:

1. Función sigmoidea binaria

Una función sigmoidea binaria tiene la forma: $y_{out}=f(x)=\frac{1}{1+e^{-kx}}$

, donde k = parámetro de inclinación o pendiente. Al variar el valor de k, se puede obtener una función sigmoidea con diferentes pendientes. Tiene un rango de (0,1). La pendiente de origen es k/4. A medida que el valor de k se vuelve muy grande, la función sigmoidea se convierte en una función de umbral.

2. Función sigmoidea bipolar

Una función sigmoidea bipolar es de la forma $y_{out}=f(x)=\frac{1-e^{-kx}}{1+e^{-kx}}$

El rango de valores de las funciones sigmoideas puede variar según la aplicación. Sin embargo, el rango de (-1,+1) es el más comúnmente adoptado.

E. Función Tangente Hiperbólica: Es de naturaleza bipolar. Es una función de activación ampliamente adoptada para un tipo especial de red neuronal conocida como Backpropagation Network. La función tangente hiperbólica es de la forma

$y_{out}=f(x)\frac{e^x-e^-x}{e^x+e^-x}$

Esta función es similar a la función sigmoidea bipolar.

Publicación traducida automáticamente

Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta