Dado un gráfico no dirigido con N vértices y M aristas, la tarea es encontrar la diferencia absoluta entre la suma de los grados de los Nodes de grado impar y los Nodes de grado par en un gráfico no dirigido.
Ejemplos:
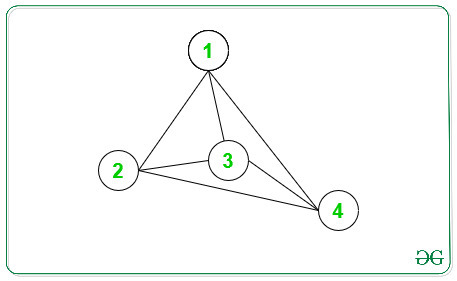
Entrada: N = 4, bordes [][] = { { 1, 2 }, { 1, 3 }, { 1, 4 }, { 2, 3 }, { 2, 4 }, { 3, 4 } }
Salida : 12
Explicación:
A continuación se muestra el gráfico de la información anterior:
Node -> Grado
1 -> 3
2 -> 3
3 -> 3
4 -> 3
Suma de Node de grado impar = 3 + 3 + 3 + 3 = 12
Suma de Node de grado par = 0
Diferencia = 12Entrada: N = 5, bordes[][] = { { 1, 2 }, { 1, 3 }, { 2, 4 }, { 2, 5 } }
Salida: 4
Acercarse:
- Para cada vértice, el grado se puede calcular por la longitud de la Lista de Adyacencia del gráfico dado en el vértice correspondiente.
- Cuente la suma de los grados de los Nodes de grado impar y los Nodes de grado par e imprima la diferencia.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation to print the
// Difference Between sum of degrees
// of odd degree nodes and even
// degree nodes.
#include <bits/stdc++.h>
using namespace std;
// Function to print the difference
// Between sum of degrees of odd
// degree nodes and even degree nodes.
int OddEvenDegree(int N, int M,
int edges[][2])
{
// To store Adjacency List of
// a Graph
vector<int> Adj[N + 1];
int EvenSum = 0;
int OddSum = 0;
// Make Adjacency List
for (int i = 0 ; i < M ; i++) {
int x = edges[i][0];
int y = edges[i][1];
Adj[x].push_back(y);
Adj[y].push_back(x);
}
// Traverse each vertex
for (int i = 1; i <= N; i++) {
// Find size of Adjacency List
int x = Adj[i].size();
// If length of Adj[i] is
// an odd number, add
// length in OddSum
if (x % 2 != 0)
{
OddSum += x;
}
else
{
// If length of Adj[i] is
// an even number, add
// length in EvenSum
EvenSum += x;
}
}
return abs(OddSum - EvenSum);
}
// Driver code
int main()
{
// Vertices and Edges
int N = 4, M = 6;
// Edges
int edges[M][2] = { { 1, 2 }, { 1, 3 }, { 1, 4 },
{ 2, 3 }, { 2, 4 }, { 3, 4 } };
// Function Call
cout<< OddEvenDegree(N, M, edges);
return 0;
}
Java
// Java implementation to print the
// difference between sum of degrees
// of odd degree nodes and even
// degree nodes.
import java.util.*;
class GFG{
// Function to print the difference
// between sum of degrees of odd
// degree nodes and even degree nodes.
static int OddEvenDegree(int N, int M,
int edges[][])
{
// To store adjacency list
// of a graph
@SuppressWarnings("unchecked")
Vector<Integer> []Adj = new Vector[N + 1];
for(int i = 0; i < N + 1; i++)
{
Adj[i] = new Vector<Integer>();
}
int EvenSum = 0;
int OddSum = 0;
// Make adjacency list
for(int i = 0; i < M; i++)
{
int x = edges[i][0];
int y = edges[i][1];
Adj[x].add(y);
Adj[y].add(x);
}
// Traverse each vertex
for(int i = 1; i <= N; i++)
{
// Find size of adjacency list
int x = Adj[i].size();
// If length of Adj[i] is
// an odd number, add
// length in OddSum
if (x % 2 != 0)
{
OddSum += x;
}
else
{
// If length of Adj[i] is
// an even number, add
// length in EvenSum
EvenSum += x;
}
}
return Math.abs(OddSum - EvenSum);
}
// Driver code
public static void main(String[] args)
{
// Vertices and edges
int N = 4, M = 6;
// Edges
int edges[][] = { { 1, 2 }, { 1, 3 }, { 1, 4 },
{ 2, 3 }, { 2, 4 }, { 3, 4 } };
// Function call
System.out.print(OddEvenDegree(N, M, edges));
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 implementation to print the # Difference Between sum of degrees # of odd degree nodes and even # degree nodes. # Function to print the difference # Between sum of degrees of odd # degree nodes and even degree nodes. def OddEvenDegree(N, M, edges): # To store Adjacency # List of a Graph Adj = [[] for i in range(N + 1)] EvenSum = 0; OddSum = 0; # Make Adjacency List for i in range(M): x = edges[i][0]; y = edges[i][1]; Adj[x].append(y); Adj[y].append(x); # Traverse each vertex for i in range(1, N + 1): # Find size of # Adjacency List x = len(Adj[i]) # If length of Adj[i] is # an odd number, add # length in OddSum if (x % 2 != 0): OddSum += x; else: # If length of Adj[i] is # an even number, add # length in EvenSum EvenSum += x; return abs(OddSum - EvenSum); # Driver code if __name__ == "__main__": # Vertices and Edges N = 4 M = 6 # Edges edges = [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]] # Function Call print(OddEvenDegree(N, M, edges)); # This code is contributed by rutvik_56
C#
// C# implementation to print the
// difference between sum of degrees
// of odd degree nodes and even
// degree nodes.
using System;
using System.Collections.Generic;
class GFG{
// Function to print the difference
// between sum of degrees of odd
// degree nodes and even degree nodes.
static int OddEvenDegree(int N, int M,
int [,]edges)
{
// To store adjacency list
// of a graph
List<int> []Adj = new List<int>[N + 1];
for(int i = 0; i < N + 1; i++)
{
Adj[i] = new List<int>();
}
int EvenSum = 0;
int OddSum = 0;
// Make adjacency list
for(int i = 0; i < M; i++)
{
int x = edges[i, 0];
int y = edges[i, 1];
Adj[x].Add(y);
Adj[y].Add(x);
}
// Traverse each vertex
for(int i = 1; i <= N; i++)
{
// Find size of adjacency list
int x = Adj[i].Count;
// If length of Adj[i] is
// an odd number, add
// length in OddSum
if (x % 2 != 0)
{
OddSum += x;
}
else
{
// If length of Adj[i] is
// an even number, add
// length in EvenSum
EvenSum += x;
}
}
return Math.Abs(OddSum - EvenSum);
}
// Driver code
public static void Main(String[] args)
{
// Vertices and edges
int N = 4, M = 6;
// Edges
int [,]edges = {{1, 2}, {1, 3}, {1, 4},
{2, 3}, {2, 4}, {3, 4}};
// Function call
Console.Write(OddEvenDegree(N, M, edges));
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// Javascript implementation to print the
// Difference Between sum of degrees
// of odd degree nodes and even
// degree nodes.
// Function to print the difference
// Between sum of degrees of odd
// degree nodes and even degree nodes.
function OddEvenDegree(N, M, edges)
{
// To store Adjacency List of
// a Graph
var Adj = Array.from(Array(N+1), ()=>Array());
var EvenSum = 0;
var OddSum = 0;
// Make Adjacency List
for (var i = 0 ; i < M ; i++) {
var x = edges[i][0];
var y = edges[i][1];
Adj[x].push(y);
Adj[y].push(x);
}
// Traverse each vertex
for (var i = 1; i <= N; i++) {
// Find size of Adjacency List
var x = Adj[i].length;
// If length of Adj[i] is
// an odd number, add
// length in OddSum
if (x % 2 != 0)
{
OddSum += x;
}
else
{
// If length of Adj[i] is
// an even number, add
// length in EvenSum
EvenSum += x;
}
}
return Math.abs(OddSum - EvenSum);
}
// Driver code
// Vertices and Edges
var N = 4, M = 6;
// Edges
var edges = [ [ 1, 2 ], [ 1, 3 ], [ 1, 4 ],
[ 2, 3 ], [ 2, 4 ], [ 3, 4 ] ];
// Function Call
document.write( OddEvenDegree(N, M, edges));
</script>
12
Publicación traducida automáticamente
Artículo escrito por saurabhshadow y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA