Suma de primeros N números naturales que no son potencias de K

Dados dos enteros  y  , la tarea es encontrar la suma de todos los números dentro del rango [1, n] excluyendo los números que son potencias positivas de k , es decir, los números k, k ² , k ³ y así sucesivamente .
Ejemplos: 
 

Entrada: n = 10, k = 3 
Salida: 43 
1 + 2 + 4 + 5 + 6 + 7 + 8 + 10 = 43 
Se excluyen 3 y 9 por ser potencias de 3
Entrada: n = 11, k = 2 
Salida : 52 
 

Acercarse: 
 

• Almacene la suma de los primeros 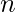 números naturales en una variable,  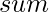es decir , sum = (n * (n + 1)) / 2 .
• Ahora, para cada poder positivo de los 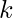 cuales es menor que  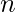, restarlo de la  .
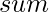• Imprime el valor de la variable 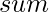 al final.

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to find the sum of
// first n natural numbers which are
// not positive powers of k
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;
 
    int power = k;
    while (power <= n) {
 
        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;
 
        // next power of k
        power *= k;
    }
 
    return total_sum;
}
 
// Driver code
int main()
{
    int n = 11, k = 2;
 
    cout << find_sum(n, k);
 
    return 0;
}

// Java program to find the sum of
// first n natural numbers which are
// not positive powers of k
import java.io.*;
 
class GFG {
   
 
 
// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
static int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;
 
    int power = k;
    while (power <= n) {
 
        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;
 
        // next power of k
        power *= k;
    }
 
    return total_sum;
}
 
// Driver code
 
    public static void main (String[] args) {
        int n = 11, k = 2;
 
    System.out.println(find_sum(n, k));
    }
}
// This code is contributed by inder_verma..

# Python 3 program to find the sum of
# first n natural numbers which are
# not positive powers of k
 
# Function to return the sum of
# first n natural numbers which are
# not positive powers of k
def find_sum(n, k):
 
    # sum of first n natural numbers
    total_sum = (n * (n + 1)) // 2
    power = k
    while power <= n:
 
        # subtract all positive powers
        # of k which are less than n
        total_sum -= power
 
        # next power of k
        power *= k
    return total_sum
 
# Driver code
n = 11; k = 2
print(find_sum(n, k))
 
# This code is contributed
# by Shrikant13

// C# program to find the sum of
// first n natural numbers which are
// not positive powers of k
using System;
 
class GFG {
 
 
 
// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
static int find_sum(int n, int k)
{
    // sum of first n natural numbers
    int total_sum = (n * (n + 1)) / 2;
 
    int power = k;
    while (power <= n) {
 
        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;
 
        // next power of k
        power *= k;
    }
 
    return total_sum;
}
 
// Driver code
 
    public static void Main () {
        int n = 11, k = 2;
 
    Console.WriteLine(find_sum(n, k));
    }
}
// This code is contributed by inder_verma..

<?php
// PHP program to find the sum of
// first n natural numbers which are
// not positive powers of k
 
// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
function find_sum($n, $k)
{
    // sum of first n natural numbers
    $total_sum = ($n * ($n + 1)) / 2;
 
    $power = $k;
    while ($power <= $n)
    {
 
        // subtract all positive powers
        // of k which are less than n
        $total_sum -= $power;
 
        // next power of k
        $power *= $k;
    }
 
    return $total_sum;
}
 
// Driver code
$n = 11; $k = 2;
 
echo find_sum($n, $k);
 
// This code is contributed by inder_verma..
?>

<script>
 
// Javascript program to find the sum of
// first n natural numbers which are
// not positive powers of k
 
// Function to return the sum of
// first n natural numbers which are
// not positive powers of k
function find_sum(n, k)
{
    // sum of first n natural numbers
    let total_sum = (n * (n + 1)) / 2;
 
    let power = k;
    while (power <= n) {
 
        // subtract all positive powers
        // of k which are less than n
        total_sum -= power;
 
        // next power of k
        power *= k;
    }
 
    return total_sum;
}
 
// Driver code
    let n = 11, k = 2;
 
    document.write(find_sum(n, k));
     
// This code is contributed by Mayank Tyagi
 
</script>

52

Complejidad temporal: O(log _k n), donde n y k representan el valor de los números enteros dados.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.