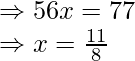Clase 11 Soluciones RD Sharma- Capítulo 22 Breve repaso del sistema cartesiano de coordenadas rectangulares- Ejercicio 22.1

Pregunta 1. Si el segmento de recta que une los puntos P(x ₁ ,y ₁ ) y Q(x ₂ ,y ₂ ) subtiende un ángulo ∅ en el origen O, demuestre que OP.OQ cos∅ = x ₁ x ₂ + y ₁ y ₂ .

Solución:

Como O es el origen, podemos obtener, OP ² = x ₁² + y ₁² y OQ ² = x ₂² + y ₂²

Además, por la fórmula de la distancia sabemos que la distancia entre dos puntos P y Q es:

PQ ² = (x ₂ – x ₁ ) ² + (y ₂ – y ₁ ) ²

Usando la fórmula del coseno, en el triángulo OPQ, tenemos

PQ ² = OP ² + OQ ² – 2 (OP). (OQ) cos∅

⇒ (x ₂ – x ₁ ) ² + (y ₂ – y ₁ ) ² = x ₁² + y ₁² + x ₂² + y ₂² – 2 (OP). (OQ) cos∅

⇒ x ₂² + x ₁² – 2 x ₂ x ₁ + y ₂² + y ₁² – 2y ₂ y ₁ = x ₁² + y ₁² + x ₂² + y ₂² – 2 (OP). (OQ) cos∅

⇒ – 2 (x ₁ x ₂ + y ₁ y ₂ ) = – 2 (OP). (OQ) cos∅

⇒ OP.OQ cos∅ = x ₁ x ₂ + y ₁ y ₂

Pregunta 2. Los vértices de un triángulo ABC son A(0,0), B (2,-1) y C (9,0). Encuentre cos B.

Solución:

Usando la fórmula del coseno, sabemos

$cos B = \frac{a^2 + c^2 - b^2}{2ac}$

Ahora, supongamos que a = BC, b = CA y c = AB son los lados del triángulo ABC.

Por lo tanto, la distancia entre dos puntos consecutivos se puede calcular como:

a = BC = $\sqrt{(9-2)^2 + (2+1)^2} = \sqrt{49 + 9} = \sqrt{58}$

b = CA = $\sqrt{(0-9)^2 + (0+2)^2} = \sqrt{81 + 4} = \sqrt{85}$

y c = AB = $\sqrt{(2-0)^2 + (-1 - 0)^2} = \sqrt{4 + 1} = \sqrt{5}$

Usando la fórmula del coseno,

$cos B = \frac{58 + 5 - 85}{2\times\sqrt{58}\times \sqrt{5}}$

$= \frac{63 - 85}{2\times\sqrt{290}}$

$= \frac{-22}{\sqrt{290}} = \frac{- 11}{\sqrt{290}}$

Por eso, $cosB = \frac{- 11}{\sqrt{290}}$

Pregunta. 3 Se dan cuatro puntos A(6,3), B(-3,5), C(4,-2) y D(x,3x) de tal forma que 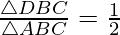$\frac{\triangle DBC}{\triangle ABC} = \frac{1}{2}$ , encuentre x.

Solución:

Conocemos la fórmula que,

área de un triángulo = $\frac{1}{2}[x_1(y_2-y_1) + x_2(y_3-y_2) + x_3(y_3-y_1)]$ , entonces

área del triángulo ABC = $\frac{1}{2}[-3(-2-3x) + 4(3x-5) + x(5+2)]$

= $\frac{1}{2}[6+ 9x+ 12x -20 + 5x +2x]$

= $\frac{1}{2}[28x -14] = 14x - 7$

Del mismo modo, el área del triángulo DBC = $\frac{1}{2}[6(5+2) - 3(-2-3) + 4(3-5)]$

= $\frac{1}{2}[42+15-8]$

= $\frac{49}{2}$

Ahora, se nos da que

$\frac{\triangle DBC}{\triangle ABC} = \frac{1}{2}$

$\Rightarrow \frac{7(2x-1)}{\frac{49}{2}} = \frac{1}{2}$

$\Rightarrow \frac{14(2x-1)}{49} = \frac{1}{2}$

$\Rightarrow \frac{28x-14}{49} = \frac{1}{2}$

$\Rightarrow 56x - 28 = 49$

$\Rightarrow 56x = 77 \\\Rightarrow x = \frac{11}{8}$

Pregunta. 4 Los puntos A(2,0), B(9,1), C(11,6) y D (4,4) son los vértices de un cuadrilátero ABCD. Determina si ABCD es un rombo o no.

Solución:

Conocemos la propiedad de un rombo de que las diagonales se bisecan en los ángulos rectos. Por lo tanto, ambas diagonales deben tener un punto medio común.

Ahora el punto medio de la línea AC = $\left ( \frac{2 + 11}{2} \right ), \left ( \frac{0 + 6}{2} \right )$ = (13/2, 3)

y el punto medio de la línea BD = $\left ( \frac{9 + 4}{2} \right ), \left ( \frac{1 + 4}{2} \right )$ = $\left ( \frac{13}{2}, \frac{5}{2} \right )$

Como ambas líneas tienen puntos medios diferentes, podemos concluir que el cuadrilátero ABCD no es un rombo.

Pregunta 5. Encuentra las coordenadas del centro del círculo inscrito en un triángulo cuyos vértices son (-36,7), (20,7) y (0,-8).

Solución:

Como la circunferencia está inscrita en un triángulo, el centro de la circunferencia se llama incentro. Sabemos que el incentro de una circunferencia (O) inscrita en un triángulo viene dado por la fórmula:

O = $\left ( \frac{ax_1 + bx_2 + cx_3}{a+b+c},\frac{ay_1 + by_2 + cy_3}{a+b+c} \right )$ , donde a, b, c son de longitud opuesta a ∠A, ∠B y ∠C respectivamente.

Por lo tanto, digamos a = BC = $\sqrt{(20-0)^2 + (7-(-8))^2} = \sqrt{20^2 + 15^2} = 25$

de manera similar, b = AC = $\sqrt{(-36-0)^2 + (7-(-8))^2} = \sqrt{36^2 + 15^2} = \sqrt{1521} = 39$

y c = AB = $\sqrt{(-36-20)^2 + (7-7)^2} = 56$

Por tanto, las coordenadas del incentro serán:

O = $\left (\frac{25(-36)+39(20)+56(0)}{25+39+56},\frac{25(7)+39(7)+56(-8)}{25+39+56}\right )$

$= \left (\frac{-1}{120},0\right )$

= (-1,0)

Por lo tanto, la coordenada del centro del círculo es (-1,0)

Pregunta 6. La base de un triángulo equilátero de lado 2a se encuentra a lo largo del eje y de manera que el punto medio de la base está en el origen. Encuentra los vértices del triángulo.

Solución:

Dado que ABC es un triángulo equilátero, tendrá ambos lados iguales, es decir, AB = BC = CA = 2a

Además, el área de un triángulo equilátero = $\frac{\sqrt{3}}{4} \times a^2$ , donde a es el lado del triángulo.

Por lo tanto, el área del triángulo dado = $\frac{\sqrt{3}}{4} \times (2a)^2 = \sqrt{3}a^2$

Además, el área de un triángulo = $\frac{1}{2}\times base \times height$

$\Rightarrow \sqrt{3}a^2 = \frac{1}{2}\times BC \times OA$

$\Rightarrow \sqrt{3}a^2 = \frac{1}{2}\times 2a \times OA$

$\Rightarrow \sqrt{3}a = OA$

Por lo tanto, las coordenadas del punto A son $\left (\sqrt{3}a,0 \right )$

de manera similar, las coordenadas del punto B son (0,-a) y las coordenadas del punto C son (0,a)

Por tanto, los vértices de un triángulo son (0,a), (0,-a) y $\left (-\sqrt{3}a,0 \right )$ o (0,a), (0.-a) y $\left (\sqrt{3}a,0 \right )$

Pregunta 7. Encuentra la distancia entre P(x1,y1) y Q(x2,y2) cuando (i) PQ es paralela al eje y, (ii) PQ es paralela al eje x.

Solución:

Nos dan dos puntos P(x1,y1) y Q(x2,y2),

(i) cuando la línea PQ es paralela al eje y, podemos concluir que la coordenada x será constante ⇒ x2 = x1

Por lo tanto, usando la fórmula de la distancia:

PQ = $\sqrt{(x2-x1)^2 + (y2-y1)^2} = \sqrt{(0)^2 + (y2-y1)^2} = |y2-y1|$

(ii) cuando la línea PQ es paralela al eje x, podemos concluir que la coordenada y será constante ⇒ y2 = y1

Por lo tanto, usando la fórmula de la distancia:

PQ = $\sqrt{(x2-x1)^2 + (y2-y1)^2} = \sqrt{(x2-x1)^2 + (0)^2} = |x2-x1|$

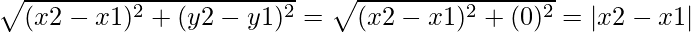
Pregunta 8. Encuentra un punto en el eje x, que sea equidistante del punto (7,6) y (3,4).

Solución:

Como se indica en la pregunta, deje que el punto C arbitrario que se encuentra en el eje x tenga la coordenada (x,0). Ahora, este punto es equidistante de las coordenadas (7,6) y (3,4), por lo tanto, al usar la fórmula de distancia, obtenemos

$\sqrt{(x-7)^2 + (0-6)^2} = \sqrt{(x-3)^2 + (0-4)^2}$

$\Rightarrow (x-7)^2 + (6)^2 = (x-3)^2 + (4)^2$

$\Rightarrow x^2 -14x + 49 + 36 = x^2 -6x + 9 + 16$

$\Rightarrow 8x = 60 \Rightarrow x = \frac{15}{2}$

Por lo tanto, la coordenada del punto en el eje x es $(\frac{15}{2},0)$

Publicación traducida automáticamente

Artículo escrito por saurabh48782 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Si el segmento de recta que une los puntos P(x 1 ,y 1 ) y Q(x 2 ,y 2 ) subtiende un ángulo ∅ en el origen O, demuestre que OP.OQ cos∅ = x 1 x 2 + y 1 y 2 .

Pregunta 2. Los vértices de un triángulo ABC son A(0,0), B (2,-1) y C (9,0). Encuentre cos B.

Pregunta. 3 Se dan cuatro puntos A(6,3), B(-3,5), C(4,-2) y D(x,3x) de tal forma que , encuentre x.

Pregunta. 4 Los puntos A(2,0), B(9,1), C(11,6) y D (4,4) son los vértices de un cuadrilátero ABCD. Determina si ABCD es un rombo o no.

Pregunta 5. Encuentra las coordenadas del centro del círculo inscrito en un triángulo cuyos vértices son (-36,7), (20,7) y (0,-8).

Pregunta 6. La base de un triángulo equilátero de lado 2a se encuentra a lo largo del eje y de manera que el punto medio de la base está en el origen. Encuentra los vértices del triángulo.

Pregunta 7. Encuentra la distancia entre P(x1,y1) y Q(x2,y2) cuando (i) PQ es paralela al eje y, (ii) PQ es paralela al eje x.

Pregunta 8. Encuentra un punto en el eje x, que sea equidistante del punto (7,6) y (3,4).

Deja una respuesta Cancelar la respuesta

Pregunta 1. Si el segmento de recta que une los puntos P(x ₁ ,y ₁ ) y Q(x ₂ ,y ₂ ) subtiende un ángulo ∅ en el origen O, demuestre que OP.OQ cos∅ = x ₁ x ₂ + y ₁ y ₂ .

Pregunta. 3 Se dan cuatro puntos A(6,3), B(-3,5), C(4,-2) y D(x,3x) de tal forma que $\frac{\triangle DBC}{\triangle ABC} = \frac{1}{2}$ , encuentre x.