Requisito previo: autómatas finitos , gráficos L y lo que representan
Los gráficos L pueden generar lenguajes sensibles al contexto, pero es mucho más difícil programar un lenguaje sensible al contexto que programar uno normal. Es por eso que se me ocurrió una hipótesis sobre qué tipo de L-graphs pueden generar un lenguaje regular. Pero primero, necesito presentarles lo que llamo un nido iterativo.
Como puede recordar, un nido es un camino neutral ![]() , donde
, donde ![]() y
y ![]() son ciclos y
son ciclos y ![]() el camino es neutral. Llamaremos a
el camino es neutral. Llamaremos a ![]() un nido iterativo, si
un nido iterativo, si ![]() y
y ![]() las
las ![]() rutas imprimen la misma string de símbolos varias veces, para ser más exactos
rutas imprimen la misma string de símbolos varias veces, para ser más exactos ![]() imprime
imprime ![]() ,
, ![]() imprime
imprime ![]() ,
, ![]() imprime
imprime ![]() ,
, ![]() y
y ![]() es una string de símbolos de entrada (mejor, si al menos uno de
es una string de símbolos de entrada (mejor, si al menos uno de ![]() ).
).
De esta definición surge la siguiente hipótesis.
Hipótesis: si en un L-grafo G libre de contexto todos los nidos están iterando, entonces el lenguaje definido por este L-grafo G, L(G), es regular.
Si esta hipótesis se prueba en un futuro cercano, puede cambiar mucho en la programación que hará que la creación de nuevos lenguajes de programación sea mucho más fácil de lo que ya es. La hipótesis anterior conduce al siguiente algoritmo de conversión de gráficos L libres de contexto con nidos iterativos en un NFA.
Algoritmo – Conversión de un gráfico L libre de contexto con complementos iterativos a un NFA correspondiente
Entrada – Gráfico L libre de contexto ![]() con complementos iterativos
con complementos iterativos
Salida – ![]()
- Paso 1: Los idiomas de L-graph y NFA deben ser los mismos, por lo tanto, no necesitaremos un nuevo alfabeto
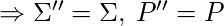 . (Comentario: construimos el L-grafo G» libre de contexto, que es igual al gráfico de inicio G’, sin nidos en conflicto)
. (Comentario: construimos el L-grafo G» libre de contexto, que es igual al gráfico de inicio G’, sin nidos en conflicto) - Paso 2: Construya Core(1, 1) para el gráfico G.
V» := {(v,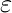 ) | v
) | v 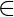 V del
V del 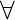 canon k
canon k 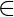 Núcleo (1, 1), v
Núcleo (1, 1), v 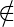 k}
k} 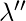 := { arcos
:= { arcos  | estados inicial y final
| estados inicial y final 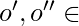 V»}
V»}
Para todos los k
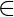 Core(1, 1):
Core(1, 1):
Paso 1′. v := 1er estado del canon k.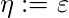 .
.
V»
Paso 2′.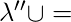 el arco del estado
el arco del estado 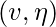 siguió este arco al nuevo estado definido con las siguientes reglas:
siguió este arco al nuevo estado definido con las siguientes reglas: 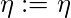 , si el paréntesis de entrada en este arco
, si el paréntesis de entrada en este arco 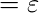 ;
; 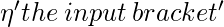 , si el paréntesis de entrada es de apertura;
, si el paréntesis de entrada es de apertura; 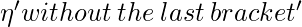 , si el corchete de entrada es un corchete de cierre
, si el corchete de entrada es un corchete de cierre
v := 2do estado del canon k
V»
Paso 3′. Repita el Paso 2′, mientras todavía haya arcos en el canon. - Paso 3: Construir Núcleo (1, 2).
Si el canon tiene 2 arcos iguales seguidos: el estado inicial y el estado final coinciden; agregamos el arco del estado dado en sí mismo, usando este arco, a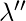 .
.
Agregue el resto en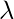 arcos v – u
arcos v – u 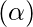 to
to 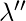 en forma de
en forma de
- Paso 4:

(Comentario: el siguiente es un algoritmo para convertir L-graph G» libre de contexto en NFA G’) - Paso 5: haga lo siguiente para cada complemento iterativo
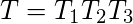 en G»:
en G»:
agregue un nuevo estado v. Cree una ruta que comience en el estado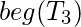 , igual a
, igual a  . Desde v hasta
. Desde v hasta  crear la ruta, igual a
crear la ruta, igual a  . Eliminar ciclos
. Eliminar ciclos  y
y  .
. - Paso 6: G’ = G», donde los arcos no se cargan con corchetes.
Para que todos los pasos anteriores queden claros, les muestro el siguiente ejemplo.  Gráfico L libre de contexto con complementos iterativos
Gráfico L libre de contexto con complementos iterativos ![Procesado por QuickLaTeX.com G = ( \{a, b, c\}, \\*\{1, 2, 3\} \\*\{( (, ) ), ( [, ] )\}, \\*\\*\{ (: \{ 1 - a - 1 \}, \\*): \{ 2 - a - 2 \}, \\*\big[: \{ 1 - b - 2 \}, \\*\big]: \{ 2 - c - 3 \}, \\*\varepsilon: \{ 1 - a - 2 \} \}, \\*\\*1, \\*\{2, 3\} \}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-237760ccc69ccc0fecd53bf643857f22_l3.png) ,
,
que determina el ![]()
 gráfico de inicio G
gráfico de inicio G 
Core(1, 1) = { 1 – a – 2 ; 1 – a, (1 – 1 – a – 2 – a, )1 – 2 ; 1 – b, (2 – 2 – c, )2 – 3 }
Núcleo(1, 2) = Núcleo(1, 1) ![]() { 1 – a, (1 – 1 – a, (1 – 1 – a – 2 – a, )1 – 2 – a, )1 – 2 }
{ 1 – a, (1 – 1 – a, (1 – 1 – a – 2 – a, )1 – 2 – a, )1 – 2 }
Paso 2: Paso 1′ – Paso 3′ ![Rendered by QuickLaTeX.com \Rightarrow\\ V'' = \{(1, \varepsilon), (2, (_2), (3, \varepsilon), (1, (_1), (2, )_1), (2, \varepsilon)\}\\* \lambda'' = \{ \\*(: \{ (1, \varepsilon) - a - (1,(); (1,() - a - (1,() \}, \\*): \{ (2, )) - a - (2, )); (2, )) - a - (2, \varepsilon) \}, \\*\big[: \{ (1, \varepsilon) - b - (2, [) \}, \\*\big]: \{ (2, [) - c - (3, \varepsilon) \}, \\*\varepsilon: \{ (1, \varepsilon) - a - (2, \varepsilon); (1,() - a - (2, )) \} \}\\ P''_0 = (1, \varepsilon)\\ F'' = \{(2, \varepsilon), (3, \varepsilon)\}\\ G'' = (\Sigma'', V'', P'', \lambda'', P''_0, F'')](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab58afb93958e34efbd4bbbcd5df155a_l3.png)
 Gráfico intermedio G»
Gráfico intermedio G» 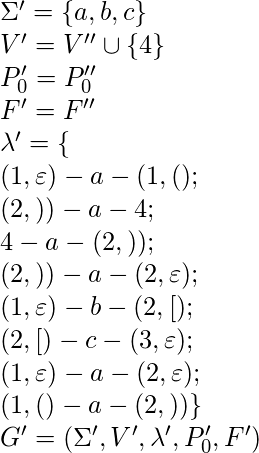
 NFA G’
NFA G’