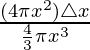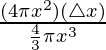Clase 12 Soluciones RD Sharma – Capítulo 14 Diferenciales, errores y aproximaciones – Ejercicio 14.1

Pregunta 1: Si y=sen x y x cambia de π/2 a 22/14, ¿cuál es el cambio aproximado en y?

Solución:

Según la condición dada,

x = π/2, y

x+△x = 22/14

△x = 22/14-x = 22/14 – π/2

Como, y = sen x

$\frac{dy}{dx}$ = cos x

$(\frac{dy}{dx})_{x=\frac{\pi}{2}}$ = coseno (π/2) = 0

△y = $(\frac{dy}{dx})_{x=\frac{\pi}{2}}$ △x

△y = 0 △x

△y = 0 (22/14 – π/2)

△y = 0

Por lo tanto, no habrá cambio en y.

Pregunta 2: El radio de una esfera se encoge de 10 a 9,8 cm. ¿Encuentra aproximadamente la disminución de su volumen?

Solución:

Según la condición dada,

Tomemos el radio como x

x = 10, y

Sea △x el error en el radio y △y el error en el volumen

x+△x = 9.8

△x = 9.8-x = 9.8-10 = -0.2

Como, Volumen de la esfera = $\frac{4}{3}\pix^3$

$\frac{dy}{dx} = \frac{4}{3}(3 \pi x^2)$ = 4πx ²

$(\frac{dy}{dx})_{x=10}$ = 4π(10) ² = 400 π

△y = $(\frac{dy}{dx})_{x=10}$ △x

△y = (400 π) (-0.2)

△y = -80 π

Por lo tanto, la disminución aproximada de su volumen será -80 π cm ³

Pregunta 3: La placa de metal circular se expande al calentarse de modo que su radio aumenta en un k%. Encuentre el aumento aproximado en el área de la placa, si el radio de la placa antes del calentamiento es de 10 cm.

Solución:

Según la condición dada,

Tomemos el radio como x

x = 10, y

Sea △x el error en el radio y △y el error en el área de la superficie

△x/x × 100 = k

△x = (k × 10)/100 = k/10

Como, Área del metal circular = πx ²

$\frac{dy}{dx}$ = π(2x) = 2πx

$(\frac{dy}{dx})_{x=10}$ = 2π(10) = 20π

△y = $(\frac{dy}{dx})_{x=10}$ △x

△y = (20 π) (k/10)

△y = 2kπ

Por lo tanto, el aumento aproximado en el área de la placa es 2kπ cm ²

Pregunta 4: Encuentra el porcentaje de error al calcular el área de la superficie de una caja cúbica si se comete un error del 1% al medir las longitudes de las aristas del cubo.

Solución:

Según la condición dada,

Sea △x el error en la longitud y △y el error en el área de la superficie

Tomemos la longitud como x

△x/x × 100 = 1

△x = x/100

x+△x = x+(x/100)

Como, área de superficie del cubo = 6x ²

$\frac{dy}{dx}$ = 6(2x) = 12x

△y = $(\frac{dy}{dx})$ △x

△y = (12x) (x/100)

△y = 0,12 x ²

Entonces, △y/y = 0.12 x ² /6 x ² = 0.02

Cambio porcentual en y = △y/y × 100 = 0,02 × 100 = 2

Por lo tanto, el porcentaje de error al calcular el área de superficie de una caja cúbica es del 2%

Pregunta 5: Si hay un error de 0.1% en la medida del radio de una esfera, encuentre aproximadamente el porcentaje de error en el cálculo del volumen de la esfera.

Solución:

Según la condición dada,

Como, Volumen de la esfera = $\frac{4}{3}\pi x^3$

Sea △x el error en el radio y △y el error en el volumen

△x/x × 100 = 0,1

△x/x = 1/1000

como, y = $\frac{4}{3}\pi x^3$

$\frac{dy}{dx} = \frac{4}{3}(3 \pi x^2)$ = 4πx ²

dy = 4πx ² dx

△y = (4πx ² ) △x

Cambio de volumen,

△y/y = $\frac{(4\pi x^2) \triangle x}{\frac{4}{3}\pi x^3}$

△y/y = $\frac{3}{x} \triangle x$

△y/y = $3(\frac{\triangle x}{x} )$ = 3(0.001) = 0.003

Cambio porcentual en y = △y/y × 100 = 0,003 × 100 = 0,3

Por tanto, aproximadamente el porcentaje de error en el cálculo del volumen de la esfera es del 0,3%

Pregunta 6: La presión p y el volumen v de un gas están conectados por la relación pv ^1.4 = constante. Encuentre el porcentaje de error en p correspondiente a una disminución de 1/2% en v.

Solución:

Según la condición dada,

$\frac{\triangle v}{v} \times 100$ = – 1/2%

pv ^1.4 = constante = k(digamos)

Tomando log en ambos lados, obtenemos

log(pv ^1.4 ) = log (k)

log(p)+log(v ^1.4 ) = log k

log(p) + 1.4 log(v) = log k

Derivando wrt v, obtenemos

$\frac{1}{p} \frac{dp}{dv} + 1.4 (\frac{1}{p}) = 0$

$\frac{dp}{p} = \frac{-1.4 dv}{v}$

Cambio porcentual en p = △p/p × 100 = $\frac{-1.4 \triangle v}{v}$ × 100 = -1.4 $(\frac{\triangle v}{v} \times 100)$

= -1.4 $(\frac{-1}{2})$

= 0,7 %

Por lo tanto, el error porcentual en p es 0.7%.

Pregunta 7: La altura de un cono aumenta en un k%, su ángulo semivertical sigue siendo el mismo. ¿Cuál es el porcentaje aproximado de aumento?

Solución:

Según la condición dada,

Sea h la altura, y el área de la superficie. V el volumen, l la altura inclinada y r el radio del cono.

Sea △h el cambio en la altura. △r el cambio en el radio de la base y △l el cambio en la altura inclinada.

Ángulo semi-vertical que permanece igual.

△h/h = △r/r = △l/l

y,

△h/h × 100 = k

△h/h × 100 = △r/r × 100 = △l/l × 100 = k

(i) en la superficie total, y

Solución:

Superficie total del cono

y = πrl + πr ²

Diferenciando ambos lados wrt r, obtenemos

$\frac{dy}{dr}$ = πl + πr $\frac{dl}{dr}$ + 2πr

$\frac{dy}{dr}$ = πl + πr $\frac{l}{r}$ + 2πr

$\frac{dy}{dr}$ = πl + πl + 2πr

$\frac{dy}{dr}$ = 2πl + 2πr = 2π(r+l)

△y = $(\frac{dy}{dr})$ △r

△y = (2π(r+l)) $(\frac{kr}{100}) = \frac{2\pi kr(r+l)}{100}$

Cambio porcentual en y = △y/y × 100 = $\frac{\frac{2\pi kr(r+l)}{100}}{\pi r(l+r)}$ × 100

= 2k %

Por lo tanto, porcentaje de aumento en el área de superficie total del cono 2k%.

(ii) en el volumen suponiendo que k es pequeño?

Solución:

Volumen del cono (y) = $\frac{1}{3}\pi r^2h$

Diferenciando ambos lados contra h, obtenemos

$\frac{dy}{dh} = \frac{1}{3}\pi$ (r2 ⁺ h(2r $\frac{dr}{dh}$ )

$\frac{dy}{dh} = \frac{1}{3}\pi$ (r2 ⁺ h(2r $\frac{r}{h}$ )

$\frac{dy}{dh} = \frac{1}{3}\pi$ ( r2 ⁺ 2r2 ⁾

$\frac{dy}{dh}$ = πr ²

△y = $(\frac{dy}{dh})$ △h

△y = (πr ² ) $(\frac{kh}{100}) = \frac{kh \pi r^2}{100}$

Cambio porcentual en y = △y/y × 100 = $\frac{\frac{kh \pi r^2}{100}}{\frac{1}{3}\pi r^2h}$ × 100

= 3k %

Por lo tanto, porcentaje de aumento en el volumen del cono 3k%.

Pregunta 8: Muestre que el error relativo al calcular el volumen de una esfera, debido a un error al medir el radio, es aproximadamente igual a tres veces el error relativo en el radio.

Solución:

Según la condición dada,

Sea △x el error en el radio y △y el error en el volumen.

Volumen del cono (y) = $\frac{4}{3}\pi x^3$

Diferenciando ambos lados de x, obtenemos

$\frac{dy}{dx} = \frac{4}{3}\pi$ ( ^3×2 )

$\frac{dy}{dx}$ = 4πx ²

△y = $(\frac{dy}{dx})$ △x

△y = (4πx ² ) (△x)

△y/y = $\frac{(4 \pi x^2) (\triangle x)}{\frac{4}{3}\pi x^3}$

△y/y = $3 \frac{\triangle x}{x}$

Por lo tanto probado!!

Pregunta 9: Usando diferenciales, encuentre los valores aproximados de lo siguiente:

(i) 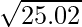$\sqrt{25.02}$

Solución:

Considerando la función como

y = f(x) = $\sqrt{x}$

Tomando x = 25, y

x+△x = 25.02

△x = 25,02-25 = 0,2

$y = \sqrt{x}$

$y_{(x=25)} = \sqrt{25} = 5$

$\frac{dy}{dx} = \frac{1}{2\sqrt{x}}$

$(\frac{dy}{dx})_{x=25} = \frac{1}{2\sqrt{25}} = \frac{1}{10}$

△y = dy = $(\frac{dy}{dx})_{x=25}$ dx

△y = $(\frac{1}{10})$ △x

△y = $(\frac{1}{10})$ (0.02) = 0.002

Por lo tanto, $\sqrt{25.02}$ = y+△y = 5 + 0.002 = 5.002

(ii) 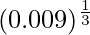$(0.009)^{\frac{1}{3}}$

Solución:

Considerando la función como

y = f(x) = $(x)^{\frac{1}{3}}$

Tomando x = 0.008, y

x+△x = 0.009

△x = 0,009-0,008 = 0,001

$y = (x)^{\frac{1}{3}}$

$y_{(x=0.008)} = (0.008)^{\frac{1}{3}} = 0.2$

$\frac{dy}{dx} = \frac{1}{3(x)^{\frac{2}{3}}}$

$(\frac{dy}{dx})_{x=0.008} = \frac{1}{3(0.008)^{\frac{2}{3}}} = \frac{1}{0.12}$

△y = dy = $(\frac{dy}{dx})_{x=0.008}$ dx

△y = $(\frac{1}{0.12})$ △x

△y = $(\frac{1}{0.12})$ (0.001) = $\frac{1}{120}$ = 0.008333

Por lo tanto, $(0.009)^{\frac{1}{3}}$ = y+△y = 0,2 + 0,008333 = 0,208333

(iii) 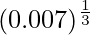$(0.007)^{\frac{1}{3}}$

Solución:

Considerando la función como

y = f(x) = $(x)^{\frac{1}{3}}$

Tomando x = 0.008, y

x+△x = 0.007

△x = 0,007-0,008 = -0,001

$y = (x)^{\frac{1}{3}}$

$y_{(x=0.008)} = (0.008)^{\frac{1}{3}}$ = 0,2

$\frac{dy}{dx} = \frac{1}{3(x)^{\frac{2}{3}}}$

$(\frac{dy}{dx})_{x=0.008} = \frac{1}{3(0.008)^{\frac{2}{3}}} = \frac{1}{0.12}$

△y = dy = $(\frac{dy}{dx})_{x=0.008}$ dx

△y = $(\frac{1}{0.12})$ △x

△y = $(\frac{1}{0.12})$ (-0.001) = $\frac{-1}{120}$ = -0.008333

Por lo tanto, $(0.007)^{\frac{1}{3}}$ = y+△y = 0,2 + (-0,008333) = 0,191667

(iv) 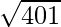$\sqrt{401}$

Solución:

Considerando la función como

y = f(x) = $\sqrt{x}$

Tomando x = 400, y

x+△x = 401

△x = 401-400 = 1

$y = \sqrt{x}$

$y_{(x=400)} = \sqrt{400} = 20$

$\frac{dy}{dx} = \frac{1}{2\sqrt{x}}$

$(\frac{dy}{dx})_{x=400} = \frac{1}{2\sqrt{400}} = \frac{1}{40}$

△y = dy = $(\frac{dy}{dx})_{x=400}$ dx

△y = $(\frac{1}{40})$ △x

△y = $(\frac{1}{40})$ (1) = 0.025

Por lo tanto, $\sqrt{401}$ = y+△y = 20 + 0,025 = 20,025

(v) 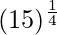$(15)^{\frac{1}{4}}$

Solución:

Considerando la función como

y = f(x) = $(x)^{\frac{1}{4}}$

Tomando x = 16, y

x+△x = 15

△x = 15-16 = -1

$y = (x)^{\frac{1}{4}}$

$y_{(x=16)} = (16)^{\frac{1}{4}} = 2$

$\frac{dy}{dx} = \frac{1}{4(x)^{\frac{3}{4}}}$

$(\frac{dy}{dx})_{x=16} = \frac{1}{4(16)^{\frac{3}{4}}} = \frac{1}{32}$

△y = dy = $(\frac{dy}{dx})_{x=16}$ dx

△y = $(\frac{1}{32})$ △x

△y = $(\frac{1}{32})$ (-1) = $\frac{-1}{32}$ = -0.03125

Por lo tanto, $(15)^{\frac{1}{4}}$ = y+△y = 0,2 + (-0,03125) = 1,96875

(vi) 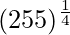$(255)^{\frac{1}{4}}$

Solución:

Considerando la función como

y = f(x) = $(x)^{\frac{1}{4}}$

Tomando x = 256, y

x+△x = 255

△x = 255-256 = -1

$y = (x)^{\frac{1}{4}}$

$y_{(x=256)} = (256)^{\frac{1}{4}}$ = 4

$\frac{dy}{dx} = \frac{1}{4(x)^{\frac{3}{4}}}$

$(\frac{dy}{dx})_{x=256} = \frac{1}{4(256)^{\frac{3}{4}}} = \frac{1}{256}$

△y = dy = $(\frac{dy}{dx})_{x=256}$ dx

△y = $(\frac{1}{256})$ △x

△y = $(\frac{1}{256})$ (-1) = $\frac{-1}{256}$ = -0.003906

Por lo tanto, $(255)^{\frac{1}{4}}$ = y+△y = 0,2 + (-0,003906) = 3,9961

(vii) 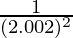$\frac{1}{(2.002)^2}$

Solución:

Considerando la función como

y = f(x) = $\frac{1}{x^2}$

Tomando x = 2, y

x+△x = 2.002

△x = 2.002-2 = 0.002

$y = \frac{1}{x^2}$

$y_{(x=2)} = \frac{1}{2^2} = \frac{1}{4}$

$\frac{dy}{dx} = \frac{-2}{x^3}$

$(\frac{dy}{dx})_{x=2} = \frac{-2}{2^3} = \frac{-1}{4}$

△y = dy = $(\frac{dy}{dx})_{x=2}$ dx

△y = $(\frac{-1}{4})$ △x

△y = $(\frac{-1}{4})$ (0.002) = -0.0005

Por lo tanto, $\frac{1}{(2.002)^2}$ = y+△y = $\frac{1}{4}$ + (-0.005) = 0.2495

(viii) log _e 4.04, siendo log ₁₀ 4=0.6021 y log ₁₀ e=0.4343

Solución:

Considerando la función como

y = f(x) = log _e x

Tomando x = 4, y

x+△x = 4.04

△x = 4-4,04 = 0,04

y = logaritmo _e x

$y_{(x=4)}$ = logaritmo _e 4 = $\frac{log_{10}4}{log_{10}e} = \frac{0.6021}{0.4343}$ = 1.386368

$\frac{dy}{dx} = \frac{1}{x}$

$(\frac{dy}{dx})_{x=4} = \frac{1}{4}$

△y = dy = $(\frac{dy}{dx})_{x=4}$ dx

△y = $(\frac{1}{4})$ △x

△y = $(\frac{1}{4})$ (0.04) = 0.01

Por lo tanto, log _e 4.04 = y+△y = 1.386368 + 0.01 = 1.396368

(ix) log _e 10.02, dado que log _e 10=2.3026

Solución:

Considerando la función como

y = f(x) = log _e x

Tomando x = 10, y

x+△x = 10.02

△x = 10,02-10 = 0,02

y = logaritmo _e x

$y_{(x=10)}$ = logaritmo _e 10 = 2,3026

$\frac{dy}{dx} = \frac{1}{x}$

$(\frac{dy}{dx})_{x=10} = \frac{1}{10}$

△y = dy = $(\frac{dy}{dx})_{x=10}$ dx

△y = $(\frac{1}{10})$ △x

△y = $(\frac{1}{10})$ (0.02) = 0.002

Por lo tanto, log _e 10.02 = y+△y = 2.3026 + 0.002 = 2.3046

(x) log ₁₀ 10.1, siendo log ₁₀ e=0.4343

Solución:

Considerando la función como

y = f(x) = registro ₁₀ x

Tomando x = 10, y

x+△x = 10.1

△x = 10,1-10 = 0,1

y = registro ₁₀ x = $\frac{log_ex}{log_e10}$

$y_{(x=10)}$ = registro ₁₀ 10 = 1

$\frac{dy}{dx} = \frac{1}{2.3025x}$

$(\frac{dy}{dx})_{x=10} = \frac{1}{23,025}$

△y = dy = $(\frac{dy}{dx})_{x=10}$ dx

△y = $(\frac{1}{23.025})$ △x

△y = $(\frac{1}{23.025})$ (0.1) = 0.004343

Por lo tanto, log _e 10.1 = y+△y = 1 + 0.004343 = 1.004343

(xi) cos 61°, dado que sen 60°=0,86603 y 1°=0,01745 radianes.

Solución:

Considerando la función como

y = f(x) = cos x

Tomando x = 60°, y

x+△x = 61°

△x = 61°-60° = 1° = 0,01745 radianes

y = cos x

$y_{(x=60 \degree)}$ = cos 60° = 0,5

$\frac{dy}{dx}$ = – sen x

$(\frac{dy}{dx})_{x=60\degree}$ = – sen 60° = -0.86603

△y = dy = $(\frac{dy}{dx})_{x=60\degree}$ dx

△y = (-0.86603) △x

△y = (-0,86603) (0,01745) = -0,01511

Por lo tanto, cos 61° = y+△y = 0,5 + (-0,01511) = 0,48489

(xii) 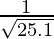$\frac{1}{\sqrt{25.1}}$

Solución:

Considerando la función como

y = f(x) = $\frac{1}{\sqrt{x}}$

Tomando x = 25, y

x+△x = 25.1

△x = 25,1-25 = 0,1

$y = \frac{1}{\sqrt{x}}$

$y_{(x=25)} = \frac{1}{\sqrt{25}} = \frac{1}{5}$

$\frac{dy}{dx} = \frac{-1}{2(x)^{\frac{3}{2}}}$

$(\frac{dy}{dx})_{x=25} = \frac{-1}{2(25)^{\frac{3}{2}}} = \frac{-1}{250}$

△y = dy = $(\frac{dy}{dx})_{x=25}$ dx

△y = $(\frac{-1}{250})$ △x

△y = $(\frac{-1}{250})$ (0.1) = $\frac{-1}{2500}$ = -0.0004

Por lo tanto, $\frac{1}{\sqrt{25.1}}$ = y+△y = $\frac{1}{5}$ + (-0.0004) = 0.1996

(xii) 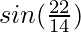$sin (\frac{22}{14})$

Solución:

Considerando la función como

y = f(x) = sen x

Tomando x = 22/7, y

x+△x = 22/14

△x = 22/14-22/7 = -22/14

pecado (-22/14) = -1

y = sen x

$y_{(x=22/7)}$ = pecado (22/7) = 0

$\frac{dy}{dx}$ = cos x

$(\frac{dy}{dx})_{x=22/7}$ = porque (22/7)= -1

△y = dy = $(\frac{dy}{dx})_{x=22/7}$ dx

△y = (-1) △x

△y = (-1) (-1) = 1

Por lo tanto, sen(22/14) = 0+1 = 1

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 14 Diferenciales, errores y aproximaciones – Ejercicio 14.1 | Serie 1

Pregunta 1: Si y=sen x y x cambia de π/2 a 22/14, ¿cuál es el cambio aproximado en y?

Pregunta 2: El radio de una esfera se encoge de 10 a 9,8 cm. ¿Encuentra aproximadamente la disminución de su volumen?

Pregunta 3: La placa de metal circular se expande al calentarse de modo que su radio aumenta en un k%. Encuentre el aumento aproximado en el área de la placa, si el radio de la placa antes del calentamiento es de 10 cm.

Pregunta 4: Encuentra el porcentaje de error al calcular el área de la superficie de una caja cúbica si se comete un error del 1% al medir las longitudes de las aristas del cubo.

Pregunta 5: Si hay un error de 0.1% en la medida del radio de una esfera, encuentre aproximadamente el porcentaje de error en el cálculo del volumen de la esfera.

Pregunta 6: La presión p y el volumen v de un gas están conectados por la relación pv ^1.4 = constante. Encuentre el porcentaje de error en p correspondiente a una disminución de 1/2% en v.

Pregunta 7: La altura de un cono aumenta en un k%, su ángulo semivertical sigue siendo el mismo. ¿Cuál es el porcentaje aproximado de aumento?

(i) en la superficie total, y

(ii) en el volumen suponiendo que k es pequeño?

Pregunta 8: Muestre que el error relativo al calcular el volumen de una esfera, debido a un error al medir el radio, es aproximadamente igual a tres veces el error relativo en el radio.

Pregunta 9: Usando diferenciales, encuentre los valores aproximados de lo siguiente:

(i) $\sqrt{25.02}$

(ii) $(0.009)^{\frac{1}{3}}$

(iii) $(0.007)^{\frac{1}{3}}$

(iv) $\sqrt{401}$

(v) $(15)^{\frac{1}{4}}$

(vi) $(255)^{\frac{1}{4}}$

(vii) $\frac{1}{(2.002)^2}$

(viii) log _e 4.04, siendo log ₁₀ 4=0.6021 y log ₁₀ e=0.4343

(ix) log _e 10.02, dado que log _e 10=2.3026

(x) log ₁₀ 10.1, siendo log ₁₀ e=0.4343

(xi) cos 61°, dado que sen 60°=0,86603 y 1°=0,01745 radianes.

(xii) $\frac{1}{\sqrt{25.1}}$

(xii) $sin (\frac{22}{14})$

Deja una respuesta Cancelar la respuesta

Pregunta 1: Si y=sen x y x cambia de π/2 a 22/14, ¿cuál es el cambio aproximado en y?

Pregunta 2: El radio de una esfera se encoge de 10 a 9,8 cm. ¿Encuentra aproximadamente la disminución de su volumen?

Pregunta 3: La placa de metal circular se expande al calentarse de modo que su radio aumenta en un k%. Encuentre el aumento aproximado en el área de la placa, si el radio de la placa antes del calentamiento es de 10 cm.

Pregunta 4: Encuentra el porcentaje de error al calcular el área de la superficie de una caja cúbica si se comete un error del 1% al medir las longitudes de las aristas del cubo.

Pregunta 5: Si hay un error de 0.1% en la medida del radio de una esfera, encuentre aproximadamente el porcentaje de error en el cálculo del volumen de la esfera.

Pregunta 6: La presión p y el volumen v de un gas están conectados por la relación pv 1.4 = constante. Encuentre el porcentaje de error en p correspondiente a una disminución de 1/2% en v.

Pregunta 7: La altura de un cono aumenta en un k%, su ángulo semivertical sigue siendo el mismo. ¿Cuál es el porcentaje aproximado de aumento?

(i) en la superficie total, y

(ii) en el volumen suponiendo que k es pequeño?

Pregunta 8: Muestre que el error relativo al calcular el volumen de una esfera, debido a un error al medir el radio, es aproximadamente igual a tres veces el error relativo en el radio.

Pregunta 9: Usando diferenciales, encuentre los valores aproximados de lo siguiente:

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii) log e 4.04, siendo log 10 4=0.6021 y log 10 e=0.4343

(ix) log e 10.02, dado que log e 10=2.3026

(x) log 10 10.1, siendo log 10 e=0.4343

(xi) cos 61°, dado que sen 60°=0,86603 y 1°=0,01745 radianes.

(xii)

(xii)

Deja una respuesta Cancelar la respuesta

Pregunta 6: La presión p y el volumen v de un gas están conectados por la relación pv ^1.4 = constante. Encuentre el porcentaje de error en p correspondiente a una disminución de 1/2% en v.

(i) $\sqrt{25.02}$

(ii) $(0.009)^{\frac{1}{3}}$

(iii) $(0.007)^{\frac{1}{3}}$

(iv) $\sqrt{401}$

(v) $(15)^{\frac{1}{4}}$

(vi) $(255)^{\frac{1}{4}}$

(vii) $\frac{1}{(2.002)^2}$

(viii) log _e 4.04, siendo log ₁₀ 4=0.6021 y log ₁₀ e=0.4343

(ix) log _e 10.02, dado que log _e 10=2.3026

(x) log ₁₀ 10.1, siendo log ₁₀ e=0.4343

(xii) $\frac{1}{\sqrt{25.1}}$

(xii) $sin (\frac{22}{14})$