Una función puede verse como una fórmula matemática o una máquina que arroja una salida cuando se proporciona una entrada. La salida suele ser una versión procesada de la entrada. Las funciones inversas pueden verse como las operaciones que nos devuelven la entrada al darles la salida. En otras palabras, las funciones inversas invierten las operaciones de la función. Estos conceptos se usan en muchos lugares de las matemáticas, donde necesitamos determinar cuál fue la entrada para la salida dada. Veamos estos conceptos en detalle.
Funciones inversas
Las funciones inversas en un sentido general son el reverso de las funciones. Para una función f(x), su inversa se denota por f -1 (x). La figura muestra cómo las funciones y las funciones inversas están relacionadas entre sí. Consideremos la función f(x) = x + 3, significa que suma 3 a su entrada. Entonces, está claro que para revertir este proceso que es encontrar la entrada nuevamente a partir de la salida dada, se debe restar 3. Entonces, f -1 (x) = x – 3.

Métodos para encontrar inversas:
Consideremos una función f(x), para encontrar la función inversa f -1 (x).
- Reemplace f(x) con y.
- Ahora, reemplaza cada x con y y viceversa.
- Resuelva la ecuación formada después del paso 2 para y.
- Reemplace y con f -1 (x).
Este método se puede utilizar para calcular la inversa de la mayoría de las funciones.
Pregunta: Encuentra el inverso para f(x) = x 2 + 1.
Solución.
Para encontrar la inversa de esta función, se seguirán los mismos pasos.
f(x) = x2 + 1
⇒ y = x2 + 1
Reemplazando x con y y viceversa
⇒x = y 2 + 1
⇒ y =
Así, f -1 (x) =
Regla de composición inversa
Dado que inverse devuelve la entrada. Es fundamental verificar si la inversa que se ha calculado es correcta o no. Para hacer esto, usamos la propiedad de composición de funciones. Digamos que f(x) es una función y g(x) es su inversa. El objetivo es verificar la exactitud de la función inversa calculada g(x). Las siguientes son las dos condiciones para verificar que g(x) es la inversa de la función f(x):
- f(g(x)) = x para todas las x en el dominio de g(x).
- g(f(x)) = x para todas las x en el dominio de f(x).
Dado que f(x) y g(x) son inversas, su composición en cualquier orden crea una función que devuelve entrada por entrada. Esta función se llama función identidad.
Veamos algunos problemas con estos conceptos.
Problemas de muestra
Pregunta 1: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = 2x + 5
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) = 2x + 5
Reemplace f(x) con y,
y = 2x + 5
Reemplazar x con y y viceversa
x = 2y + 5
Resolviendo la ecuación para y,
y =
Sea la inversa g(x) =
y f(x) = 2x + 5.
f(g(x))
f(
)
⇒ 2(
) + 5
⇒x – 5 + 5
⇒x
g(f(x))
g(2x + 5)
⇒ (
)
⇒x
Por lo tanto, Verificado.
Pregunta 2: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = x2
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) = x2
Reemplace f(x) con y,
y = x2
Reemplazar x con y y viceversa
x = y 2
Resolviendo la ecuación para y,
y = √x
Sea la inversa g(x) = √x y f(x) = x 2
f(g(x))
f(√x)
⇒ (√x) 2
⇒x
g(f(x))
√( x2 )
⇒ x
Por lo tanto, Verificado.
Pregunta 3: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = ![]()
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) =
Reemplace f(x) con y,
y =
Reemplazar x con y y viceversa
x =
Resolviendo la ecuación para y,
y = 7x + 3
Sea la inversa g(x) = 7x + 3 y f(x) =
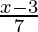
f(g(x))
f(7x + 3)
⇒
⇒x
g(f(x))
g(
)
⇒ 7(
) + 3
⇒x
Por lo tanto, Verificado.
Pregunta 4: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = registro(x)
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) = registro(x)
Reemplace f(x) con y,
y = registro (x)
Reemplazar x con y y viceversa
x = registro (y)
Resolviendo la ecuación para y,
y = e x
Sea la inversa g(x) = e x y f(x) = log(x)
f(g(x))
f( ex )
⇒ log(e x )
⇒x
g(f(x))
⇒e log(x)
⇒ x
Por lo tanto, Verificado.
Pregunta 5: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = x3 + 1
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) = x3 + 1
Reemplace f(x) con y,
y = x 3 + 1
Reemplazar x con y y viceversa
x = y 3 + 1
Resolviendo la ecuación para y,
y =
Sea la inversa g(x) =
y f(x) = x 3 + 1
f(g(x))
f(
)
⇒ (
) 3 + 1
⇒x
g(f(x))
⇒
![Rendered by QuickLaTeX.com \sqrt[3]{(x^3 + 1) - 1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdfe8a48f52a74427b3883cc0e7ce391_l3.png)
⇒ x
Por lo tanto, Verificado.
Pregunta 6: Encuentra el inverso de la siguiente función y compruébalo con las propiedades mencionadas anteriormente.
f(x) = e x + 1
Responder:
Siguiendo los pasos mencionados en los métodos anteriores.
f(x) = e x + 1
Reemplace f(x) con y,
y = e x + 1
Reemplazar x con y y viceversa
x = e y + 1
Resolviendo la ecuación para y,
y = registro (x -1)
Sea la inversa g(x) = log(x – 1) y f(x) = e x + 1
f(g(x))
f(registro(x – 1))
⇒ e log(x – 1) + 1
⇒x
g(f(x))
⇒ g(ex + 1)
⇒ log(e x + 1 – 1)
⇒ x
Por lo tanto, Verificado.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA