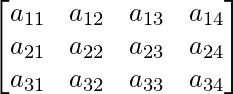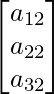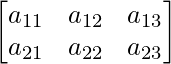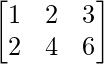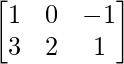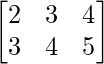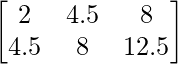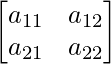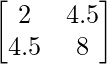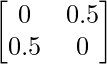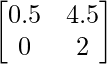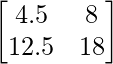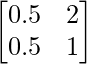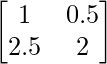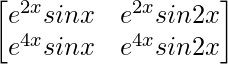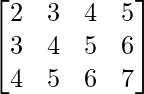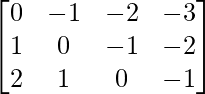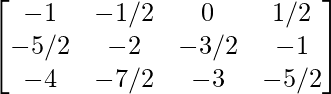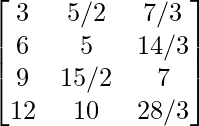Clase 12 Soluciones RD Sharma – Capítulo 5 Álgebra de Arrays – Ejercicio 5.1

Pregunta 1: Si una array tiene 8 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Y si tiene 5 elementos?

Solución:

Parte 1:

Sea la array de dimensión mxn.

Por lo tanto, mxn = 8.

Luego, todo lo que tenemos que hacer es encontrar los divisores de 8, que son: 1, 2, 4, 8.

Así, los órdenes posibles son: 1×8, 8×1, 2×4 y 4×2.

Parte 2:

Siguiendo un enfoque similar:

Ya que, mxn = 5.

Los divisores de 5 son: 1,5.

Así, los órdenes posibles son: 1×5 y 5×1.

Pregunta 2(i): Si A = [a _ij ] = $\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _jj ] = $\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₂₂ +b ₂₁ .

Solución:

Sabemos que todo elemento en una array A de dimensiones mxn puede ser direccionado como a _ij , donde 1≤ i ≤ m y 1 ≤ j ≤ n.

Por lo tanto, a ₂₂ es el segundo ^elemento en la ^segunda fila de A , y b ₂₁ es el ^primer elemento en la ^segunda fila de B.

Eso implica, a ₂₂ + b ₂₁ = 4 + (-3) = 1.

Pregunta 2(ii): Si A = [a _ij ]= 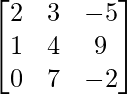$\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _ij ] = 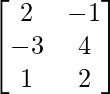$\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₁₁ b ₁₁ + a ₂₂ b ₂₂ .

Solución:

Como se vio en la pregunta anterior, todo elemento de una array A de dimensiones mxn puede ser direccionado como a _ij , donde 1≤ i ≤ m y 1 ≤ j ≤ n.

De este modo,

a ₁₁ = 1 ^primer elemento en la 1 ^primera fila de A = 2.

a ₂₂ = 2 ^do elemento en la 2 ^da fila de A = 4.

b ₁₁ = 1 ^primer elemento en la 1 ^primera fila de B = 2.

b ₂₂ = ^2º elemento en la ^2ª fila de B = 4.

Eso implica, a ₁₁ b ₁₁ + a ₂₂ b ₂₂ = (2×2) + (4×4) = 4 + 16 = 20.

Pregunta 3: Sea A una array de orden 3×4. Si R1 denota la primera fila de A y C2 denota su segunda columna, entonces determine los órdenes de las arrays R1 y C2.

Solución:

Dado, A es una array de orden 3×4.

Sabemos que una array de orden mxn tiene m filas y n columnas.

Por lo tanto, A contiene 3 filas y cada fila contiene 4 elementos.

$\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$

Ahora, si R1 es una fila, tiene 4 elementos y, por lo tanto, su orden se puede escribir como 1 × 4, $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \end{bmatrix}$

Y de manera similar, si C2 es una columna, tendrá 3 filas, cada una con 1 elemento, y por lo tanto su orden es 3×1, $\begin{bmatrix} a_{12} \\ a_{22} \\ a_{32} \\ \end{bmatrix}$

Pregunta 4(i): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = ix j.

Solución:

Sabemos que A es una array de orden 2×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}$

Dado que cada elemento es un producto de su número de fila y número de columna (ixj):

un ₁₁ = 1 un ₁₂ = 2 un ₁₃ = 3

un ₂₁ = 2 un ₂₂ = 4 un ₂₃ = 6

Por lo tanto, A puede representarse como: $\begin{bmatrix} 1 & 2 & 3\\ 2 & 4 & 6 \end{bmatrix}$

Pregunta 4(ii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = 2i – j.

Solución:

Sabemos que A es una array de orden 2×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}$

Dado que cada elemento se puede definir como (2 x (número de fila)) – número de columna:

un ₁₁ = 1 un ₁₂ = 0 un ₁₃ = -1

un ₂₁ = 3 un ₂₂ = 2 un ₂₃ = 1

Por lo tanto, A puede representarse como: $\begin{bmatrix} 1 & 0 & -1\\ 3 & 2 & 1 \end{bmatrix}$

Pregunta 4(iii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = i + j.

Solución:

Sabemos que A es una array de orden 2×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}$

Dado que cada elemento se puede definir como la suma de su número de fila y número de columna:

un ₁₁ = 2 un ₁₂ = 3 un ₁₃ = 4

un ₂₁ = 3 un ₂₂ = 4 un ₂₃ = 5

Por lo tanto, A puede representarse como: $\begin{bmatrix} 2 & 3 & 4\\ 3 & 4 & 5 \end{bmatrix}$

Pregunta 4(iv): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por : a _ij = 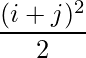$\dfrac{(i+j)^2}{2}$ .

Solución:

Sabemos que A es una array de orden 2×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{(row\,number + column\,number)^2}{2}$ ,

un ₁₁ = 2 un ₁₂ = 4,5 un ₁₃ = 8

21 = 4,5 ₂₂ = 8 ₂₃₌ 12,5

Por lo tanto, A puede representarse como: $\begin{bmatrix} 2 & 4.5 & 8\\ 4.5 & 8 & 12.5 \end{bmatrix}$

Pregunta 5(i): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 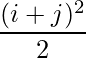$\dfrac{(i+j)^2}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{(row\,number + column\,number)^2}{2}$ ,

un ₁₁ = 2 un ₁₂ = 4,5

un ₂₁ = 4,5 un ₂₂ = 8

Por lo tanto, A puede representarse como: $\begin{bmatrix} 2 & 4.5\\ 4.5 & 8 \end{bmatrix}$

Pregunta 5(ii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 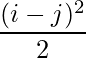$\dfrac{(i-j)^2}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{(row\,number - column\,number)^2}{2}$ ,

un ₁₁ = 0 un ₁₂ = 0,5

un ₂₁ = 0,5 un ₂₂ = 0

Por lo tanto, A puede representarse como: $\begin{bmatrix} 0 & 0.5\\ 0.5 & 0 \end{bmatrix}$

Pregunta 5(iii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 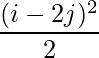$\dfrac{(i-2j)^2}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{(row\,number - 2\times column\,number)^2}{2}$ ,

un ₁₁ = 0,5 un ₁₂ = 4,5

un ₂₁ = 0 un ₂₂ = 2

Por lo tanto, A puede representarse como: $\begin{bmatrix} 0.5 & 4.5\\ 0 & 2 \end{bmatrix}$

Pregunta 5(iv): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 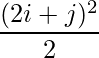$\dfrac{(2i+j)^2}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{(2\times row\,number + column\,number)^2}{2}$ ,

un ₁₁ = 4,5 un ₁₂ = 8

un ₂₁ = 12,5 un ₂₂ = 18

Por lo tanto, A puede representarse como: $\begin{bmatrix} 4.5 & 8\\ 12.5 & 18 \end{bmatrix}$

Pregunta 5(v): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 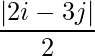$\dfrac{|2i-3j|}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$ ,

Dado que cada elemento se puede definir como : $\dfrac{|2\times row\,number - 3\times column\,number|}{2}$ ,

un ₁₁ = 0,5 un ₁₂ = 2

un ₂₁ = 0,5 un ₂₂ = 1

Por lo tanto, A puede representarse como: $\begin{bmatrix} 0.5 & 2\\ 0.5 & 1 \end{bmatrix}$

Pregunta 5(vi): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 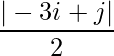$\dfrac{|-3i+j|}{2}$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$ ,

Dado que cada elemento se puede definir como : $\dfrac{|-3\times row\,number + column\,number|}{2}$ ,

un ₁₁ = 1 un ₁₂ = 0,5

un ₂₁ = 2,5 un ₂₂ = 2

Por lo tanto, A puede representarse como: $\begin{bmatrix} 1 & 0.5\\ 2.5 & 2 \end{bmatrix}$

Pregunta 5(vii) Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : 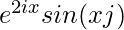$e^{2ix}sin(xj)$ .

Solución:

Sabemos que A es una array de orden 2×2.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$ ,

Dado que cada elemento se puede definir como : $e^{2x\times row\,number} sin(x\times column\,number)$ ,

a ₁₁ = e ^2x senx a ₁₂ = e ^2x sen2x

a ₂₁ = e ^4x senx a ₂₂ = e ^4x sen2x

Por lo tanto, A puede representarse como: $\begin{bmatrix} e^{2x}sinx & e^{2x}sin2x\\ e^{4x}sinx & e^{4x}sin2x \end{bmatrix}$

Pregunta 6(i): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i + j .

Solución:

A es una array de orden 3×4.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$ ,

Dado que cada elemento se puede definir como: (número de fila + número de columna),

un ₁₁ = 2 un ₁₂ = 3 un ₁₃ = 4 un ₁₄ = 5

un ₂₁ = 3 un ₂₂ = 4 un ₂₃ = 5 un ₂₄ = 6

un ₃₁ = 4 un ₃₂ = 5 un ₃₃ = 6 un ₃₄ = 7

Por lo tanto, A puede representarse como: $\begin{bmatrix} 2 & 3 & 4 & 5\\ 3 & 4 & 5 & 6\\ 4 & 5 & 6 & 7\\ \end{bmatrix}$

Pregunta 6(ii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i – j.

Solución:

A es una array de orden 3×4.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$ ,

Dado que cada elemento se puede definir como: (número de fila – número de columna),

un ₁₁ = 0 un ₁₂ = -1 un ₁₃ = -2 un ₁₄ = -3

un ₂₁ = 1 un ₂₂ = 0 un ₂₃ = -1 un ₂₄ = -2

un ₃₁ = 2 un ₃₂ = 1 un ₃₃ = 0 un ₃₄ = -1

Por lo tanto, A puede representarse como: $\begin{bmatrix} 0 & -1 & -2 & -3\\ 1 & 0 & -1 & -2\\ 2 & 1 & 0 & -1\\ \end{bmatrix}$

Pregunta 6(iii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = 2i .

Solución:

A es una array de orden 3×4.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$ ,

Dado que cada elemento se puede definir como: (2 x número de fila),

un ₁₁ = 2 un ₁₂ = 2 un ₁₃ = 2 un ₁₄ = 2

un ₂₁ = 4 un ₂₂ = 4 un ₂₃ = 4 un ₂₄ = 4

un ₃₁ = 6 un ₃₂ = 6 un ₃₃ = 6 un ₃₄ = 6

Por lo tanto, A puede representarse como: $\begin{bmatrix} 2 & 2 & 2 & 2\\ 4 & 4 & 4 & 4\\ 6 & 6 & 6 & 6\\ \end{bmatrix}$

Pregunta 6(iv): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = j.

Solución:

A es una array de orden 3×4.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$ ,

Dado que cada elemento se puede definir como: (número de columna),

un ₁₁ = 1 un ₁₂ = 2 un ₁₃ = 3 un ₁₄ = 4

un ₂₁ = 1 un ₂₂ = 2 un ₂₃ = 3 un ₂₄ = 4

un ₃₁ = 1 un ₃₂ = 2 un ₃₃ = 3 un ₃₄ = 4

Por lo tanto, A puede representarse como: $\begin{bmatrix} 1 & 2 & 3 & 4\\ 1 & 2 & 3 & 4\\ 1 & 2 & 3 & 4\\ \end{bmatrix}$

Pregunta 6(v): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = 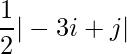$\dfrac{1}{2}|-3i+j|$ .

Solución:

A es una array de orden 3×4.

Por lo tanto, A se puede representar como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ \end{bmatrix}$ ,

Dado que cada elemento se puede definir como : $\dfrac{1}{2}|-3\times row\,number+column\,number|$ ,

un ₁₁ = -1 un ₁₂ = -1/2 un ₁₃ = 0 un ₁₄ = 1/2

a ₂₁ = -5/2 a ₂₂ = -2 a ₂₃ = -3/2 a ₂₄ = -1

un ₃₁ = -4 un ₃₂ = -7/2 un ₃₃ = -3 un ₃₄ = -5/2

Por lo tanto, A puede representarse como: $\begin{bmatrix} -1 & -1/2 & 0 & 1/2\\ -5/2 & -2 & -3/2 & -1\\ -4 & -7/2 & -3 & -5/2\\ \end{bmatrix}$

Pregunta 7(i): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = 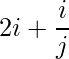$2i+\dfrac{i}{j}$ .

Solución:

A es una array de orden 4×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{bmatrix}$

Dado que cada elemento se puede definir como : $(2\times row\,number)+\dfrac{row\,number}{column\,number}$ ,

un ₁₁ = 3 un ₁₂ = 5/2 un ₁₃ = 7/3

un ₂₁ = 6 un ₂₂ = 5 un ₂₃ = 14/3

un ₃₁ = 9 un ₃₂ = 15/2 un ₃₃ = 7

un ₄₁ = 12 un ₄₂ = 10 un ₄₃ = 28/3

Por lo tanto, A puede representarse como: $\begin{bmatrix} 3 & 5/2 & 7/3 \\ 6 & 5 & 14/3 \\ 9 & 15/2 & 7 \\ 12 & 10 & 28/3 \end{bmatrix}$

Pregunta 7(ii): Construya una array de 4×3 A = [a _ij ] cuyos a _ij estén dados por : a _ij = 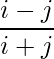$\dfrac{i-j}{i+j}$ .

Solución:

A es una array de orden 4×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{bmatrix}$

Dado que cada elemento se puede definir como : $\dfrac{row\,number-column\,number}{row\,number+column\,number}$ ,

un ₁₁ = 0 un ₁₂ = -1/3 un ₁₃ = -1/2

un ₂₁ = 1/3 un ₂₂ = 0 un ₂₃ = -1/5

un ₃₁ = 1/2 un ₃₂ = 1/5 un ₃₃ = 0

un ₄₁ = 3/5 un ₄₂ = 1/3 un ₄₃ = 1/7

Por lo tanto, A puede representarse como: $\begin{bmatrix} 0 & -1/3 & -1/2 \\ 1/3 & 0 & -1/5 \\ 1/2 & 1/5 & 0 \\ 3/5 & 1/3 & 1/7 \end{bmatrix}$

Pregunta 7(iii): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = i.

Solución:

A es una array de orden 4×3.

Por lo tanto, A puede representarse como: $\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{bmatrix}$

Dado que cada elemento se puede definir como: (número de fila)

un ₁₁ = 1 un ₁₂ = 1 un ₁₃ = 1

un ₂₁ = 2 un ₂₂ = 2 un ₂₃ = 2

un ₃₁ = 3 un ₃₂ = 3 un ₃₃ = 3

un ₄₁ = 4 un ₄₂ = 4 un ₄₃ = 4

Por lo tanto, A puede representarse como: $\begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 3 & 3 & 3 \\ 4 & 4 & 4 \end{bmatrix}$

Pregunta 8: Encuentra x, y, a y b si: 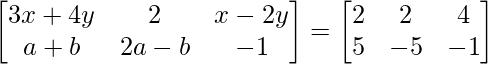$\begin{bmatrix} 3x+4y & 2 & x-2y \\ a+b & 2a-b & -1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 2 & 4 \\ 5 & -5 & -1 \\ \end{bmatrix}$

Solución:

Podemos ver que tanto la array del lado izquierdo (LHS) como la array del lado derecho (RHS) son de la dimensión 2×3.

Dado que la array en LHS es igual a la array en RHS, cada elemento en LHS en el índice (i, j) debe ser igual a cada elemento en RHS en el índice (i, j).

Por lo tanto, equiparando cada elemento en RHS a LHS:

a ₁₁ : 3x+4y = 2 ………………(eq.1) a ₁₂ : 2 = 2 a ₁₃ : x-2y = 4 ………………(eq.2)

a ₂₁ : a+b = 5 ………………(eq.3) a ₂₂ : 2a-b = -5………………..(eq.4) a ₂₃ : -1 = -1

Así, (eq.1) y (eq.2) forman un sistema de ecuaciones que comprende las variables x e y.

Resolviendo (eq.1) y (eq.2): (eq.1) + 2x(eq.2)

=> (3x+2x) + (4y-2(2y)) = 2+ (2(4))

=> 5x = 10

=> x = 2

Sustituyendo (x=2) en (eq.1) :

=> (3(2)) + 4y = 2

=> 4y = 2-6 = -4

=> y=-1

De manera similar, (eq.3) y (eq.4) forman un sistema de ecuaciones que comprende las variables ay b.

Resolviendo (eq.3) y (eq.4) : (eq.1) + (eq.2)

=> (a+2a) + (bb) = 5 – 5

=> 3a = 0

=> un = 0

Sustituyendo (a=0) en (eq.3):

=> 0 + segundo = 5

=> segundo = 5

Así, a=0, b=5, x=2 e y=-1.

Pregunta 9: Calcula x, y, ayb si : 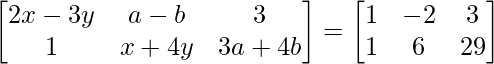$\begin{bmatrix} 2x-3y & a-b & 3 \\ 1 & x+4y & 3a+4b \\ \end{bmatrix} = \begin{bmatrix} 1 & -2 & 3 \\ 1 & 6 & 29 \\ \end{bmatrix}$ .

Solución:

Podemos ver que tanto la array del lado izquierdo (LHS) como la array del lado derecho (RHS) son de la dimensión 2×3.

Dado que la array del LHS es igual a la array del RHS, cada elemento del LHS en el índice (i, j) debe ser igual a cada elemento del RHS en el índice (i, j).

Por lo tanto, equiparando cada elemento en RHS a LHS:

a ₁₁ : 2x-3y = 1………………(ecuación 1) a ₁₂ : ab = -2………………(ecuación 2) a ₁₃ : 3 = 3

a ₂₁ : 1 = 1 a ₂₂ : x+4y = 6………………..(ecuación 3) a ₂₃ : 3a+4b = 29………………(ecuación 4)

Por lo tanto, (eq.1) y (eq.3) forman un sistema de ecuaciones que comprende las variables x e y.

Resolviendo (eq.1) y (eq.2) : (eq.1) – 2x(eq.2)

=> (2x-2x) + (-3y-2(4y)) = 1- (2(6))

=> -11 años = -11

=> y = 1

Sustituyendo (y=1) en (eq.1) :

=> 2x – 3(1) = 1

=> 2x = 3+1 = 4

=> x = 2

De manera similar, (eq.2) y (eq.4) forman un sistema de ecuaciones que comprende las variables a y b.

Resolviendo (eq.2) y (eq.4) : 4x(eq.1) + (eq.2)

=> (4a+3a) + (-4(b)+4b) = 4(-2) + 29

=> 7a = 21

=> un = 3

Sustituyendo (a=3) en (eq.2) :

=> 3 – b = -2

=>b = 5

Así, a=3, b=5, x=2 e y=1.

Pregunta 10: Encuentra a, b, c y d si: 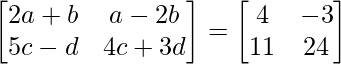$\begin{bmatrix} 2a+b & a-2b \\ 5c-d & 4c+3d \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ 11 & 24 \\ \end{bmatrix}$

Solución:

Podemos ver que tanto la array del lado izquierdo (LHS) como la array del lado derecho (RHS) son de la dimensión 2×2.

Dado que la array en LHS es igual a la array en RHS, cada elemento en LHS en el índice (i, j) debe ser igual a cada elemento en RHS en el índice (i, j).

Por lo tanto, equiparando cada elemento en RHS a LHS:

a ₁₁ : 2a+b = 4 ………….(ecuación 1)

a ₁₂ : a-2b = -3 …………(ecuación 2)

a ₂₁ : 5c-d = 11 …………(ecuación 3)

a ₂₂ : 4c+3d = 24 ……..(ecuación 4)

Por lo tanto, (eq.1) y (eq.2) forman un sistema de ecuaciones que comprende las variables a y b.

Resolviendo (eq.1) y (eq.2) : (eq.1) – 2x(eq.2)

=> (2a-2a) + (b+4b) = 4 + (-2(-3))

=> 5b = 10

=> segundo = 2

Sustituyendo (b=2) en (eq.1) :

=> 2a + 2 = 4

=> 2a = 4-2 = 2

=> un=1

De manera similar, (eq.3) y (eq.4) forman un sistema de ecuaciones que comprende las variables c y d.

Resolviendo (eq.3) y (eq.4) : 3x(eq.1) + (eq.2)

=> (15c+4c) + (-3d+3d) = 33 + 24

=> 19c = 57

=> c = 3

Sustituyendo (c=3) en (eq.4) :

=> (4(3)) + 3d = 24

=>3d = 24 – 12 = 12

=> re = 4

Así, a=1, b=2, c=3 y d=4.

Publicación traducida automáticamente

Artículo escrito por isha412k y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 5 Álgebra de Arrays – Ejercicio 5.1 | Serie 1

Pregunta 1: Si una array tiene 8 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Y si tiene 5 elementos?

Pregunta 2(i): Si A = [a _ij ] = $\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _jj ] = $\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₂₂ +b ₂₁ .

Pregunta 2(ii): Si A = [a _ij ]= $\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _ij ] = $\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₁₁ b ₁₁ + a ₂₂ b ₂₂ .

Pregunta 3: Sea A una array de orden 3×4. Si R1 denota la primera fila de A y C2 denota su segunda columna, entonces determine los órdenes de las arrays R1 y C2.

Pregunta 4(i): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = ix j.

Pregunta 4(ii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = 2i – j.

Pregunta 4(iii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = i + j.

Pregunta 4(iv): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por : a _ij = $\dfrac{(i+j)^2}{2}$ .

Pregunta 5(i): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i+j)^2}{2}$ .

Pregunta 5(ii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i-j)^2}{2}$ .

Pregunta 5(iii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i-2j)^2}{2}$ .

Pregunta 5(iv): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(2i+j)^2}{2}$ .

Pregunta 5(v): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{|2i-3j|}{2}$ .

Pregunta 5(vi): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{|-3i+j|}{2}$ .

Pregunta 5(vii) Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $e^{2ix}sin(xj)$ .

Pregunta 6(i): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i + j .

Pregunta 6(ii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i – j.

Pregunta 6(iii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = 2i .

Pregunta 6(iv): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = j.

Pregunta 6(v): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = $\dfrac{1}{2}|-3i+j|$ .

Pregunta 7(i): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = $2i+\dfrac{i}{j}$ .

Pregunta 7(ii): Construya una array de 4×3 A = [a _ij ] cuyos a _ij estén dados por : a _ij = $\dfrac{i-j}{i+j}$ .

Pregunta 7(iii): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = i.

Pregunta 8: Encuentra x, y, a y b si: $\begin{bmatrix} 3x+4y & 2 & x-2y \\ a+b & 2a-b & -1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 2 & 4 \\ 5 & -5 & -1 \\ \end{bmatrix}$

Pregunta 9: Calcula x, y, ayb si : $\begin{bmatrix} 2x-3y & a-b & 3 \\ 1 & x+4y & 3a+4b \\ \end{bmatrix} = \begin{bmatrix} 1 & -2 & 3 \\ 1 & 6 & 29 \\ \end{bmatrix}$ .

Pregunta 10: Encuentra a, b, c y d si: $\begin{bmatrix} 2a+b & a-2b \\ 5c-d & 4c+3d \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ 11 & 24 \\ \end{bmatrix}$

Deja una respuesta Cancelar la respuesta

Pregunta 1: Si una array tiene 8 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Y si tiene 5 elementos?

Pregunta 2(i): Si A = [a ij ] = y B = [b jj ] = entonces encuentre a 22 +b 21 .

Pregunta 2(ii): Si A = [a ij ]= y B = [b ij ] = entonces encuentre a 11 b 11 + a 22 b 22 .

Pregunta 3: Sea A una array de orden 3×4. Si R1 denota la primera fila de A y C2 denota su segunda columna, entonces determine los órdenes de las arrays R1 y C2.

Pregunta 4(i): Construya una array de 2×3 A = [a ij ] cuyos elementos a ij estén dados por: a ij = ix j.

Pregunta 4(ii): Construya una array de 2×3 A = [a ij ] cuyos elementos a ij estén dados por: a ij = 2i – j.

Pregunta 4(iii): Construya una array de 2×3 A = [a ij ] cuyos elementos a ij estén dados por: a ij = i + j.

Pregunta 4(iv): Construya una array de 2×3 A = [a ij ] cuyos elementos a ij estén dados por : a ij = .

Pregunta 5(i): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(ii): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(iii): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(iv): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(v): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(vi): Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 5(vii) Construya una array de 2×2 A = [a ij ] cuyos a ij estén dados por : .

Pregunta 6(i): Construya una array de 3×4 A = [a ij ] cuyos a ij estén dados por: a ij = i + j .

Pregunta 6(ii): Construya una array de 3×4 A = [a ij ] cuyos a ij estén dados por: a ij = i – j.

Pregunta 6(iii): Construya una array de 3×4 A = [a ij ] cuyos a ij estén dados por: a ij = 2i .

Pregunta 6(iv): Construya una array de 3×4 A = [a ij ] cuyas a ij estén dadas por: a ij = j.

Pregunta 6(v): Construya una array de 3×4 A = [a ij ] cuyas a ij estén dadas por : a ij = .

Pregunta 7(i): Construya una array de 4×3 A = [a ij ] cuyas a ij estén dadas por : a ij = .

Pregunta 7(ii): Construya una array de 4×3 A = [a ij ] cuyos a ij estén dados por : a ij = .

Pregunta 7(iii): Construya una array de 4×3 A = [a ij ] cuyas a ij estén dadas por: a ij = i.

Pregunta 8: Encuentra x, y, a y b si:

Pregunta 9: Calcula x, y, ayb si : .

Pregunta 10: Encuentra a, b, c y d si:

Deja una respuesta Cancelar la respuesta

Pregunta 2(i): Si A = [a _ij ] = $\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _jj ] = $\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₂₂ +b ₂₁ .

Pregunta 2(ii): Si A = [a _ij ]= $\begin{bmatrix} 2 & 3 & -5\\ 1 & 4 & 9\\ 0 & 7 & -2 \end{bmatrix}$ y B = [b _ij ] = $\begin{bmatrix} 2 & -1\\ -3 & 4\\ 1 & 2 \end{bmatrix}$ entonces encuentre a ₁₁ b ₁₁ + a ₂₂ b ₂₂ .

Pregunta 4(i): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = ix j.

Pregunta 4(ii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = 2i – j.

Pregunta 4(iii): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por: a _ij = i + j.

Pregunta 4(iv): Construya una array de 2×3 A = [a _ij ] cuyos elementos a _ij estén dados por : a _ij = $\dfrac{(i+j)^2}{2}$ .

Pregunta 5(i): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i+j)^2}{2}$ .

Pregunta 5(ii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i-j)^2}{2}$ .

Pregunta 5(iii): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(i-2j)^2}{2}$ .

Pregunta 5(iv): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{(2i+j)^2}{2}$ .

Pregunta 5(v): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{|2i-3j|}{2}$ .

Pregunta 5(vi): Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $\dfrac{|-3i+j|}{2}$ .

Pregunta 5(vii) Construya una array de 2×2 A = [a _ij ] cuyos a _ij estén dados por : $e^{2ix}sin(xj)$ .

Pregunta 6(i): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i + j .

Pregunta 6(ii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = i – j.

Pregunta 6(iii): Construya una array de 3×4 A = [a _ij ] cuyos a _ij estén dados por: a _ij = 2i .

Pregunta 6(iv): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = j.

Pregunta 6(v): Construya una array de 3×4 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = $\dfrac{1}{2}|-3i+j|$ .

Pregunta 7(i): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por : a _ij = $2i+\dfrac{i}{j}$ .

Pregunta 7(ii): Construya una array de 4×3 A = [a _ij ] cuyos a _ij estén dados por : a _ij = $\dfrac{i-j}{i+j}$ .

Pregunta 7(iii): Construya una array de 4×3 A = [a _ij ] cuyas a _ij estén dadas por: a _ij = i.

Pregunta 8: Encuentra x, y, a y b si: $\begin{bmatrix} 3x+4y & 2 & x-2y \\ a+b & 2a-b & -1 \\ \end{bmatrix} = \begin{bmatrix} 2 & 2 & 4 \\ 5 & -5 & -1 \\ \end{bmatrix}$

Pregunta 9: Calcula x, y, ayb si : $\begin{bmatrix} 2x-3y & a-b & 3 \\ 1 & x+4y & 3a+4b \\ \end{bmatrix} = \begin{bmatrix} 1 & -2 & 3 \\ 1 & 6 & 29 \\ \end{bmatrix}$ .

Pregunta 10: Encuentra a, b, c y d si: $\begin{bmatrix} 2a+b & a-2b \\ 5c-d & 4c+3d \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ 11 & 24 \\ \end{bmatrix}$