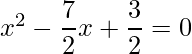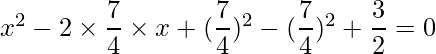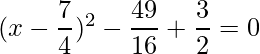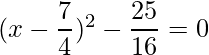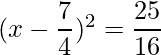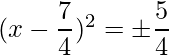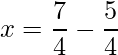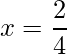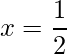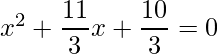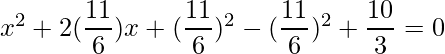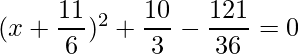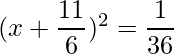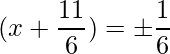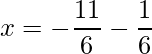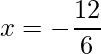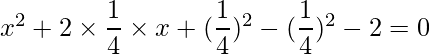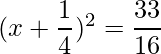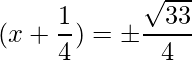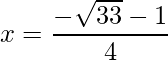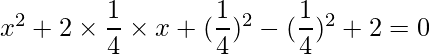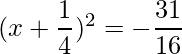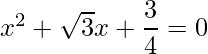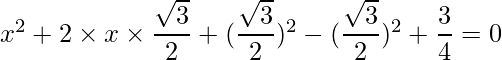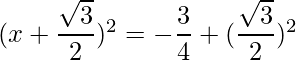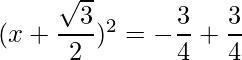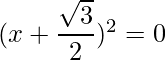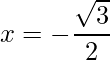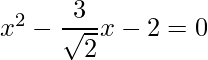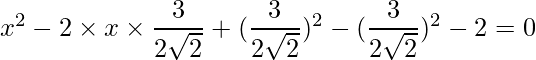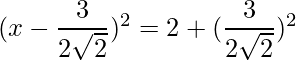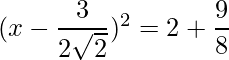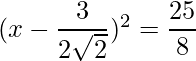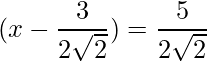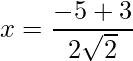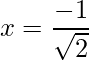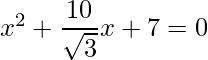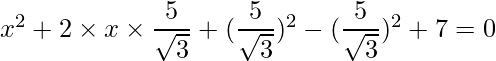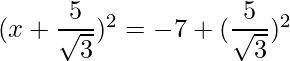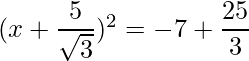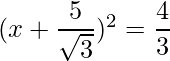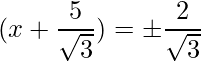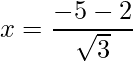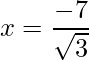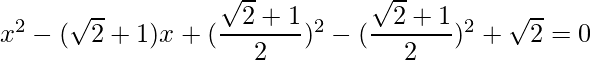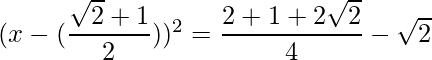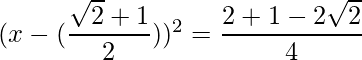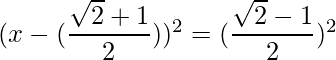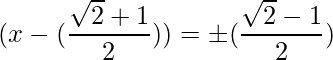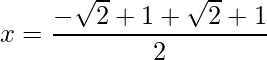Pregunta 1: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 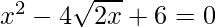 .
.
Solución:
Dado:
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=>
=>
Lo sabemos:
=>
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=> x =
y x=
=> x =
y x =
Pregunta 2: Encuentra las raíces de la siguiente cuadrática (si existen) por el método de completar el cuadrado: 2x 2 -7x+3 = 0.
Solución:
Dado: 2x 2 -7x+3 = 0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> 2x 2 -7x+3 = 0
=>
=>
Lo sabemos:
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
=>
y
=> x = 3 y
Pregunta 3: Encuentra las raíces de la siguiente cuadrática (si existen) por el método de completar el cuadrado: 3x 2 +11x+10 = 0.
Solución:
Dado: 3x 2 +11x+10 = 0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> 3×2 + 11x+10 = 0
=>
=>
Lo sabemos:
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
=>
y
=>
y x = -2
Pregunta 4: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 2x 2 +x-4 =0.
Solución:
Dado: 2x 2 +x-4 =0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> 2x 2 +x-4 =0
=>
=>
Lo sabemos:
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
Pregunta 5: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 2x 2 +x+4 =0.
Solución:
Dado: 2x 2 +x+4 =0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> 2x 2 +x+4 =0
=>
=>
Lo sabemos:
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=> El RHS es negativo, lo que implica que las raíces no son reales.
Pregunta 6: Encuentra las raíces de la siguiente cuadrática (si existen) por el método de completar el cuadrado: 4x 2 +4√3+3=0.
Solución:
Dado: 4x 2 +4√3+3=0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> 4×2 + 4√3+3=0
=>
=>
Lo sabemos,
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
El RHS es cero, lo que implica que las raíces existen y son iguales.
=>
Pregunta 7: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 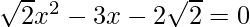 .
.
Solución:
Dado:
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=>
=>
=>
Lo sabemos,
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
=>
y
Pregunta 8: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 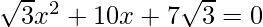 .
.
Solución:
Dado:
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=>
=>
=>
Lo sabemos,
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
=>
y
Pregunta 9: Encuentra las raíces de las siguientes cuadráticas (si existen) por el método de completar el cuadrado: 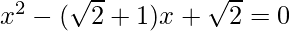 .
.
Solución:
Dado:
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=>
=>
Lo sabemos,
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=>
=>
=>
El RHS es positivo, lo que implica que las raíces existen.
=>
=>
y
=> x = √2 y x = 1
Pregunta 10: Encuentra las raíces de la siguiente ecuación cuadrática (si existen) por el método de completar el cuadrado: x 2 -4ax+4a 2 -b 2 =0.
Solución:
Dado: x 2 -4ax+4a 2 -b 2 =0
Tenemos que hacer que la ecuación sea un cuadrado perfecto.
=> x 2 -4ax+4a 2 -b 2 =0
=> x 2 −2×x×2a+(2a) 2 −b 2 =0
Lo sabemos,
=> (a−b) 2 =a 2 −2×a×b+b 2
Por lo tanto, la ecuación se puede escribir como:
=> x 2 −2×2a×x+(2a) 2 =b 2
=> (x-2a) 2 = b 2
El RHS es positivo, lo que implica que las raíces existen.
=> (x-2a) = ±b
=> x= 2a+b y x = 2a-b