Clase 10 Soluciones RD Sharma – Capítulo 8 Ecuaciones cuadráticas – Ejercicio 8.5

Pregunta 1. Encuentra el discriminante de las siguientes ecuaciones cuadráticas:

(yo) 2x ² – 5x + 3 = 0

Solución:

Dada la ecuación cuadrática: 2x ² – 5x + 3 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b = -5 y c = 3

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-5) ² – 4(2)(3)

= 25 – 24

= 1

Por lo tanto, el discriminante de la ecuación cuadrática dada es 1

(ii) x2 ⁺ 2x + 4 = 0

Solución:

Dada la ecuación cuadrática: x ² + 2x + 4 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = 2 y c = 4

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (2) ² – 4(1)(4)

= 4 – 16

= -12

Por lo tanto, el discriminante de la ecuación cuadrática dada es -12

(iii) (x – 1) (2x – 1)

Solución:

Dada la ecuación cuadrática:(x – 1)(2x – 1)

O también podemos escribir como, 2x ² – 3x + 1 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b = -3 y c = 1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-3) ² – 4(2)(1)

= 9 – 8

= 1

Por lo tanto, el discriminante de la ecuación cuadrática dada es 1

(iv) x ² – 2x + k = 0

Solución:

Dada la ecuación cuadrática: x ² – 2x + k = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = -2 y c = k

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-2) ² – 4(1)(k)

= 4 -4k

Por lo tanto, el discriminante de la ecuación cuadrática dada es 4 – 4k

(v) √3x ² + 2√2x – 2√3 = 0

Solución:

Dada la ecuación cuadrática:√3x ² + 2√2x – 2√3 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a =√3, b = 2√2 y c = -2 – 2√3

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (2√2) ² – 4√3(-2√3)

= 8 + 24

= 32

Por lo tanto, el discriminante de la ecuación cuadrática dada es 32

(vi) x ² – x + 1 = 0

Solución:

Dada la ecuación cuadrática: x ² – x + 1 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = -1 y c = 1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-1) ² – 4(1)(1)

= 1 – 4

= -3

Por lo tanto, el discriminante de la ecuación cuadrática dada es -3

Pregunta 2. A continuación, determine si la ecuación cuadrática dada tiene raíces reales y, de ser así, encuentre las raíces:

(yo) 16x ² = 24x + 1

Solución:

Ecuación cuadrática dada: 16x ² – 24x – 1 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 16, b = -24 y c = -1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-24) ² – 4(16)(-1)

= 576 + 64

= 640

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-(-24)\pm \sqrt{640}}{2(16)}$

$x=\frac{24\pm8\sqrt{1032}}{32}$

$x=\frac{3\pm \sqrt{10}}{4}$

Por lo tanto, el valor de x es

$x=\frac{3+\sqrt{10}}{4}$

$x=\frac{3-\sqrt{10}}{4}$

(ii) x ² + x + 2 = 0

Solución:

Dada la ecuación cuadrática: x ² + x + 2 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = 1 y c = 2

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (1) ² – 4(1)(2)

= 1 – 8

= -7

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación no satisface la condición dada, por lo que no tiene raíces reales.

(iii) √3x ² + 10x – 8√3 = 0

Solución:

Dada la ecuación cuadrática: √3x ² + 10x – 8√3 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = √3, b = 10 y c = -8√3

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (10) ² – 4(√3)(-8√3)

= 100 + 96

= 196

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-10\pm \sqrt{196}}{2\sqrt{3}}$

$x=\frac{-5\pm 7}{\sqrt{3}}$

Por lo tanto, el valor de x es

$x=\frac{-5+7}{\sqrt{3}}=\frac{2}{\sqrt 3}$

$x=\frac{-5-7}{\sqrt{3}}= \frac{-12}{\sqrt{3}} = -4\sqrt{3}$

(iv) 3x ² – 2x + 2 = 0

Solución:

Dada la ecuación cuadrática: 3x ² – 2x + 2 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 3, b = -2 y c = 2

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-2) ² – 4(3)(2)

= 4 – 24

= -20

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación no satisface la condición dada, por lo que no tiene raíces reales.

(v) 2x ² – 2√6x + 3 = 0

Solución:

Dada la ecuación cuadrática: 2x ² – 2√6x + 3 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b= -2√6 y c = 3

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-2√6) ² – 4(2)(3)

= 24 – 24

= 0

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x= \frac{-2\sqrt 6 \pm 0}{2(2)}$

$x=-\sqrt{\frac{3}{2}}$

(vi) 3a ² x ² + 8abx + 4b ² = 0

Solución:

Dada la ecuación cuadrática: 3a ² x ² + 8abx + 4b ² = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 3a ² , b = 8ab y c = 4b ²

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (8ab) ² – 4(3a ² )(4b ² )

= 64a ² segundo ² – 48a ² segundo ²

= 16a ² b ²

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-8ab \pm \sqrt{ 16a^2b^2}}{6a^2}$

$x=\frac{-4b \pm 2b}{3a}$

Por lo tanto, el valor de x es

$x= \frac{-4b+2b}{3a} = \frac{-2b}{3a}$

$x = \frac{-2b}{a}$

(vii) 3x ² – 2√5x – 5 = 0

Solución:

Ecuación cuadrática dada: 3x ² – 2√5x – 5 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 3, b = 2√5 y c = -5

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (2√5 ) ² – 4(3)(-5)

= 20 + 60

= 80

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-2\sqrt5 \pm \sqrt{80}}{2(3)}$

$x = \frac{-\sqrt5 \pm 2\sqrt5}{3}$

Por lo tanto, el valor de x es

x = √5 /3

x = -√5

(viii) x ² – 2x + 1 = 0

Solución:

Dada la ecuación cuadrática: x ² – 2x + 1 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = -2 y c = 1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-2) ² – 4(1)(1)

= 4 – 4

= 0

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x= \frac{-(-2)\pm \sqrt{0}}{2(1)}$

X = 1

(ix) 2x ² + 5√3x + 6 = 0

Solución:

Dada la ecuación cuadrática: 2x ² + 5√3x + 6 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b = 5√3 y c = 6

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (5√3) ² – 4(2)(6)

= 75 – 48

= 27

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-5\sqrt3 \pm \sqrt{ 27}}{2(2)} =\frac{-5\sqrt3\pm 3\sqrt 3}{4}$

Por lo tanto, el valor de x es

x = -√3 /2

x = -2√3

(x) √2x ² + 7x + 5√2 = 0

Solución:

Dada la ecuación cuadrática: √2x ² + 7x + 5√2 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = √2, b = 7 y c = 5√2

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (7) ² – 4(√2)(5√2)

= 49 – 40

= 9

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-7\pm \sqrt9}{2\sqrt2}$

Por lo tanto, el valor de x es

x = -√2

x = -5/√2

(xi) 2x ² – 2√2x + 1 = 0

Solución:

Ecuación cuadrática dada: 2x ² – 2√2x + 1 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b = -2√2 y c = 1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-2√2) ² – 4(2)(1)

= 8 – 8

= 0

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-(-2\sqrt2)\pm \sqrt 0}{2(2)} =\frac{2\sqrt2}{4}$

Por lo tanto, el valor de x es

x = 1/√2

(xii) 3x ² – 5x + 2 = 0

Solución:

Dada la ecuación cuadrática: 3x ² – 5x + 2 = 0 ….(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 3, b = -5 y c = 2

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-5) ² – 4(3)(2)

= 25 – 24

= 1

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{-(-5)\pm \sqrt 1}{2(3)} = \frac{5\pm1}{6}$

Por lo tanto, el valor de x es

X = 1

X = 2/3

Pregunta 3. Resolver para x:

(yo) 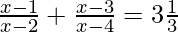$\frac{x-1}{x-2}+\frac{x-3}{x-4}=3\frac{1}{3}$ , x ≠ 2, 4

Solución:

Dado: $\frac{x-1}{x-2}+\frac{x-3}{x-4}=3\frac{1}{3}$

También podemos escribir como

$\frac{(x-1)(x-4)+(x-3)(x-2)}{(x-2)(x-4)}=\frac{10}{3}$

6x ² – 30x + 30 = 10x ² – 60x + 80

4x ² – 30x + 50 = 0

2x ² – 15x + 25 = 0 …(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 2, b = -15 y c = 25

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-15) ² – 4(2)(25)

= 225 – 200

= 25

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{15\pm 5}{4}$

Por lo tanto, el valor de x es

x = 5

x = 5/2

(ii) x + 1/x = 3, x ≠ 0

Solución:

Dado: x + 1/x = 3

También podemos escribir como

x ² – 3x + 1 = 0 …(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = -3 y c = 1

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-3) ² – 4(1)(1)

= 9 – 4

= 5

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{3\pm \sqrt 5}{2}$

Por lo tanto, el valor de x es

$x=\frac{3+\sqrt5}{2}$

$x=\frac{3-\sqrt5}{2}$

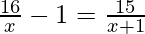(iii) $\frac{16}{x}-1 = \frac{15}{x+1}$ , x ≠ 0, -1

Solución:

Dado: $\frac{16}{x}-1 = \frac{15}{x+1}$

También podemos escribir como

$\frac{16-x}{x}= \frac{15}{x+1}$

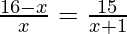
(16 – x)(x + 1) = 15x

15x + 16 – x2 ^– 15x = 0

16 – x2 ⁼ 0

x ² – 16 = 0 ……(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = 0 y c = -16

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (0) ² – 4(1)(-16)

= 64

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{0\pm \sqrt {64}}{2(1)} =\frac{\pm8}{2}=\pm4$

Por lo tanto, el valor de x es

x = ±4

(iv) 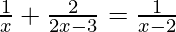$\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$ , x ≠ 0, 3/2, 2

Solución:

Dado: $\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$

También podemos escribir como

$\frac{(2x-3)+2x}{x(2x-3)}= \frac{1}{x-2}$

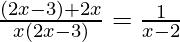
(x-2)(4x-3) = x(2x-3)

x ² – 4x + 3 = 0 ……(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = -4 y c = 3

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (-4) ² – 4(1)(3)

= 4

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{4\pm \sqrt {4}}{2(1)} =\frac{\pm6}{2}=\pm3$

Por lo tanto, el valor de x es

x = ±3

(v) 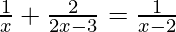$\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$ , x ≠ 3, -5

Solución:

Dado: $\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$

También podemos escribir como

$\frac{(x+5)-(x-3)}{(x-3)(x+5)}= \frac{1}{6}$

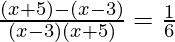
(x – 3)(x + 5) = 6 x 8

x2 ⁺ 2x – 63 = 0 ……(1)

Como sabemos que la forma general de la ecuación cuadrática es

ax ² + bx + c = 0 ….(2)

Al comparar la ecuación (1) y (2), obtenemos

Aquí, a = 1, b = 2 y c = -63

Ahora encontramos el discriminante(D) = b ² – 4ac

D = (2) ² – 4(1)(-63)

= 256

Como sabemos que para que una ecuación cuadrática tenga raíz real debe satisfacer el D >= 0

Aquí, nuestra ecuación satisface la condición dada, por lo que tiene raíces reales.

Ahora encontramos las raíces reales usando la fórmula dada:

$x= \frac{-b\pm \sqrt{D}}{2a}$

Ponga los valores de b, D, a en la fórmula dada, obtenemos

$x=\frac{2\pm \sqrt {256}}{2(1)} =\frac{\pm18}{2}=\pm9$

Por lo tanto, el valor de x es

x = ±9

Publicación traducida automáticamente

Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el discriminante de las siguientes ecuaciones cuadráticas:

(yo) 2x 2 – 5x + 3 = 0

(ii) x2 + 2x + 4 = 0

(iii) (x – 1) (2x – 1)

(iv) x 2 – 2x + k = 0

(v) √3x 2 + 2√2x – 2√3 = 0

(vi) x 2 – x + 1 = 0

Pregunta 2. A continuación, determine si la ecuación cuadrática dada tiene raíces reales y, de ser así, encuentre las raíces:

(yo) 16x 2 = 24x + 1

(ii) x 2 + x + 2 = 0

(iii) √3x 2 + 10x – 8√3 = 0

(iv) 3x 2 – 2x + 2 = 0

(v) 2x 2 – 2√6x + 3 = 0

(vi) 3a 2 x 2 + 8abx + 4b 2 = 0

(vii) 3x 2 – 2√5x – 5 = 0

(viii) x 2 – 2x + 1 = 0

(ix) 2x 2 + 5√3x + 6 = 0

(x) √2x 2 + 7x + 5√2 = 0

(xi) 2x 2 – 2√2x + 1 = 0

(xii) 3x 2 – 5x + 2 = 0

Pregunta 3. Resolver para x:

(yo) , x ≠ 2, 4

(ii) x + 1/x = 3, x ≠ 0

(iii) , x ≠ 0, -1

(iv) , x ≠ 0, 3/2, 2

(v) , x ≠ 3, -5

Deja una respuesta Cancelar la respuesta

(yo) 2x ² – 5x + 3 = 0

(ii) x2 ⁺ 2x + 4 = 0

(iv) x ² – 2x + k = 0

(v) √3x ² + 2√2x – 2√3 = 0

(vi) x ² – x + 1 = 0

(yo) 16x ² = 24x + 1

(ii) x ² + x + 2 = 0

(iii) √3x ² + 10x – 8√3 = 0

(iv) 3x ² – 2x + 2 = 0

(v) 2x ² – 2√6x + 3 = 0

(vi) 3a ² x ² + 8abx + 4b ² = 0

(vii) 3x ² – 2√5x – 5 = 0

(viii) x ² – 2x + 1 = 0

(ix) 2x ² + 5√3x + 6 = 0

(x) √2x ² + 7x + 5√2 = 0

(xi) 2x ² – 2√2x + 1 = 0

(xii) 3x ² – 5x + 2 = 0

(yo) $\frac{x-1}{x-2}+\frac{x-3}{x-4}=3\frac{1}{3}$ , x ≠ 2, 4

(iii) $\frac{16}{x}-1 = \frac{15}{x+1}$ , x ≠ 0, -1

(iv) $\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$ , x ≠ 0, 3/2, 2

(v) $\frac{1}{x}+\frac{2}{2x-3} = \frac{1}{x-2}$ , x ≠ 3, -5