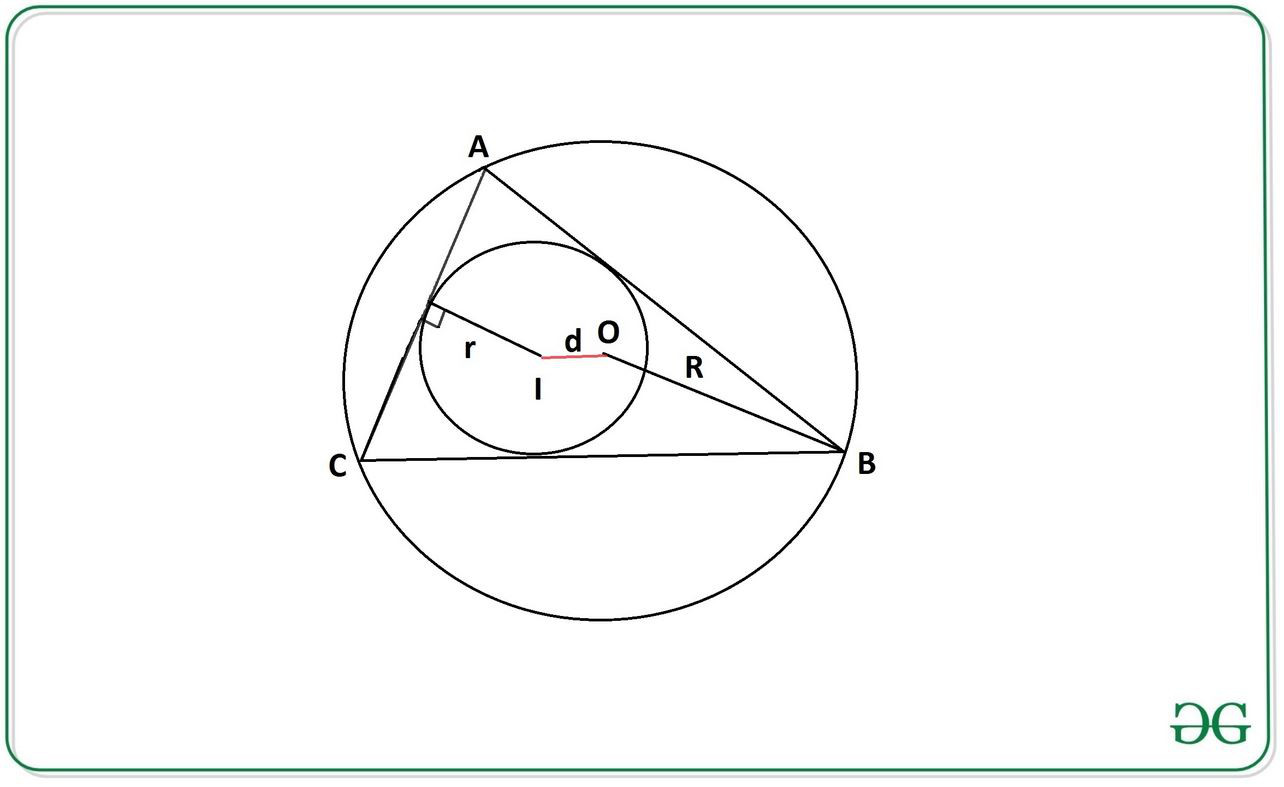
Dados dos enteros r y R que representan la longitud de Inradius y Circumradius respectivamente, la tarea es calcular la distancia d entre Incenter y Circumcenter.
Inradius El inradius( r ) de un triángulo regular ( ABC ) es el radio de la circunferencia inscrita (con centro en l), que es la circunferencia más grande que cabe dentro del triángulo.
Circunradio: El circunradio (R) de un triángulo es el radio del círculo circunscrito (que tiene el centro en O) de ese triángulo.
Ejemplos:
Entrada: r = 2, R = 5
Salida: 2,24Entrada: r = 5, R = 12
Salida: 4,9
Enfoque:
el problema se puede resolver utilizando el teorema de Euler en geometría, que establece que la distancia entre el incentro y el circuncentro de un triángulo se puede calcular mediante la ecuación:
A continuación se muestra la implementación del enfoque anterior:
C++14
// C++14 program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function returns the required distance
double distance(int r, int R)
{
double d = sqrt(pow(R, 2) -
(2 * r * R));
return d;
}
// Driver code
int main()
{
// Length of Inradius
int r = 2;
// Length of Circumradius
int R = 5;
cout << (round(distance(r, R) * 100.0) / 100.0);
}
// This code is contributed by sanjoy_62
Java
// Java program for the above approach
import java.util.*;
class GFG{
// Function returns the required distance
static double distance(int r,int R)
{
double d = Math.sqrt(Math.pow(R, 2) -
(2 * r * R));
return d;
}
// Driver code
public static void main(String[] args)
{
// Length of Inradius
int r = 2;
// Length of Circumradius
int R = 5;
System.out.println(Math.round(
distance(r, R) * 100.0) / 100.0);
}
}
// This code is contributed by offbeat
Python3
# Python3 program for the above approach import math # Function returns the required distance def distance(r,R): d = math.sqrt( (R**2) - (2 * r * R)) return d # Driver Code # Length of Inradius r = 2 # Length of Circumradius R = 5 print(round(distance(r,R),2))
C#
// C# program for the above approach
using System;
class GFG{
// Function returns the required distance
static double distance(int r, int R)
{
double d = Math.Sqrt(Math.Pow(R, 2) -
(2 * r * R));
return d;
}
// Driver code
public static void Main(string[] args)
{
// Length of Inradius
int r = 2;
// Length of Circumradius
int R = 5;
Console.Write(Math.Round(
distance(r, R) * 100.0) / 100.0);
}
}
// This code is contributed by rutvik_56
Javascript
<script>
// Javascript program for
// the above approach
// Function returns the required distance
function distance(r, R)
{
let d = Math.sqrt(Math.pow(R, 2) -
(2 * r * R));
return d;
}
// Driver code
// Length of Inradius
let r = 2;
// Length of Circumradius
let R = 5;
document.write(Math.round(
distance(r, R) * 100.0) / 100.0);
// This code is contributed by susmitakundugoaldanga.
</script>
2.24
Complejidad de tiempo: O(sqrt(logn)) desde el uso de funciones incorporadas
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por divyamohan123 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA