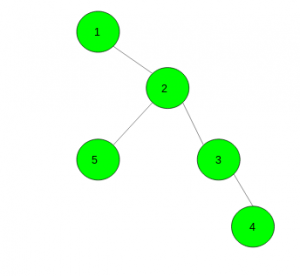
Dado un entero k y un árbol con n Nodes. La tarea es contar el número de pares distintos de vértices que tienen una distancia de exactamente k .
Ejemplos:
Entrada: k = 2
Salida: 4
Entrada: k = 3
Salida: 2
Enfoque: Este problema se puede resolver mediante programación dinámica. Para cada vértice v del árbol, calculamos valores d[v][lev] (0 <= lev <= k). Este valor indica el número de vértices que tienen la distancia lev de v. Tenga en cuenta que d[v][0] = 1.
Luego calculamos la respuesta. Para cualquier vértice v, el número de pares será un producto del número de vértices en el nivel j – 1 y el nivel k – j.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
#define N 5005
// To store vertices and value of k
int n, k;
vector<int> gr[N];
// To store number vertices at a level i
int d[N][505];
// To store the final answer
int ans = 0;
// Function to add an edge between two nodes
void Add_edge(int x, int y)
{
gr[x].push_back(y);
gr[y].push_back(x);
}
// Function to find the number of distinct
// pairs of the vertices which have a distance
// of exactly k in a tree
void dfs(int v, int par)
{
// At level zero vertex itself is counted
d[v][0] = 1;
for (auto i : gr[v]) {
if (i != par) {
dfs(i, v);
// Count the pair of vertices at
// distance k
for (int j = 1; j <= k; j++)
ans += d[i][j - 1] * d[v][k - j];
// For all levels count vertices
for (int j = 1; j <= k; j++)
d[v][j] += d[i][j - 1];
}
}
}
// Driver code
int main()
{
n = 5, k = 2;
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
// Function call
dfs(1, 0);
// Required answer
cout << ans;
return 0;
}
Java
// Java implementation of the approach
import java.util.*;
class GFG
{
static final int N = 5005;
// To store vertices and value of k
static int n, k;
static Vector<Integer>[] gr = new Vector[N];
// To store number vertices at a level i
static int[][] d = new int[N][505];
// To store the final answer
static int ans = 0;
// Function to add an edge between two nodes
static void Add_edge(int x, int y)
{
gr[x].add(y);
gr[y].add(x);
}
// Function to find the number of distinct
// pairs of the vertices which have a distance
// of exactly k in a tree
static void dfs(int v, int par)
{
// At level zero vertex itself is counted
d[v][0] = 1;
for (Integer i : gr[v])
{
if (i != par)
{
dfs(i, v);
// Count the pair of vertices at
// distance k
for (int j = 1; j <= k; j++)
ans += d[i][j - 1] * d[v][k - j];
// For all levels count vertices
for (int j = 1; j <= k; j++)
d[v][j] += d[i][j - 1];
}
}
}
// Driver code
public static void main(String[] args)
{
n = 5;
k = 2;
for (int i = 0; i < N; i++)
gr[i] = new Vector<Integer>();
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
// Function call
dfs(1, 0);
// Required answer
System.out.print(ans);
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 implementation of the approach N = 5005 # To store vertices and value of k n, k = 0, 0 gr = [[] for i in range(N)] # To store number vertices at a level i d = [[0 for i in range(505)] for i in range(N)] # To store the final answer ans = 0 # Function to add an edge between two nodes def Add_edge(x, y): gr[x].append(y) gr[y].append(x) # Function to find the number of distinct # pairs of the vertices which have a distance # of exactly k in a tree def dfs(v, par): global ans # At level zero vertex itself is counted d[v][0] = 1 for i in gr[v]: if (i != par): dfs(i, v) # Count the pair of vertices at # distance k for j in range(1, k + 1): ans += d[i][j - 1] * d[v][k - j] # For all levels count vertices for j in range(1, k + 1): d[v][j] += d[i][j - 1] # Driver code n = 5 k = 2 # Add edges Add_edge(1, 2) Add_edge(2, 3) Add_edge(3, 4) Add_edge(2, 5) # Function call dfs(1, 0) # Required answer print(ans) # This code is contributed by Mohit Kumar
C#
// C# implementation of the approach
using System;
using System.Collections.Generic;
class GFG
{
static readonly int N = 5005;
// To store vertices and value of k
static int n, k;
static List<int>[] gr = new List<int>[N];
// To store number vertices at a level i
static int[,] d = new int[N, 505];
// To store the readonly answer
static int ans = 0;
// Function to add an edge between two nodes
static void Add_edge(int x, int y)
{
gr[x].Add(y);
gr[y].Add(x);
}
// Function to find the number of distinct
// pairs of the vertices which have a distance
// of exactly k in a tree
static void dfs(int v, int par)
{
// At level zero vertex itself is counted
d[v, 0] = 1;
foreach (int i in gr[v])
{
if (i != par)
{
dfs(i, v);
// Count the pair of vertices at
// distance k
for (int j = 1; j <= k; j++)
ans += d[i, j - 1] * d[v, k - j];
// For all levels count vertices
for (int j = 1; j <= k; j++)
d[v, j] += d[i, j - 1];
}
}
}
// Driver code
public static void Main(String[] args)
{
n = 5;
k = 2;
for (int i = 0; i < N; i++)
gr[i] = new List<int>();
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
// Function call
dfs(1, 0);
// Required answer
Console.Write(ans);
}
}
// This code is contributed by Rajput-Ji
PHP
<?php
// PHP implementation of the approach
$N = 5005;
// To store vertices and value of k
$gr = array_fill(0, $N, array());
// To store number vertices
// at a level i
$d = array_fill(0, $N,
array_fill(0, 505, 0));
// To store the final answer
$ans = 0;
// Function to add an edge between
// two nodes
function Add_edge($x, $y)
{
global $gr;
array_push($gr[$x], $y);
array_push($gr[$y], $x);
}
// Function to find the number of distinct
// pairs of the vertices which have a
// distance of exactly k in a tree
function dfs($v, $par)
{
global $d, $ans, $k, $gr;
// At level zero vertex itself
// is counted
$d[$v][0] = 1;
foreach ($gr[$v] as &$i)
{
if ($i != $par)
{
dfs($i, $v);
// Count the pair of vertices
// at distance k
for ($j = 1; $j <= $k; $j++)
$ans += $d[$i][$j - 1] *
$d[$v][$k - $j];
// For all levels count vertices
for ($j = 1; $j <= $k; $j++)
$d[$v][$j] += $d[$i][$j - 1];
}
}
}
// Driver code
$n = 5;
$k = 2;
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
// Function call
dfs(1, 0);
// Required answer
echo $ans;
// This code is contributed by mits
?>
Javascript
<script>
// Javascript implementation of the approach
let N = 5005;
// To store vertices and value of k
let n, k;
let gr = new Array(N);
// To store number vertices at a level i
let d = new Array(N);
for(let i = 0 ; i < N; i++)
{
d[i] = new Array(505);
for(let j = 0; j < 505; j++)
{
d[i][j] = 0;
}
}
// To store the final answer
let ans = 0;
// Function to add an edge between two nodes
function Add_edge(x, y)
{
gr[x].push(y);
gr[y].push(x);
}
// Function to find the number of distinct
// pairs of the vertices which have a distance
// of exactly k in a tree
function dfs(v, par)
{
// At level zero vertex itself is counted
d[v][0] = 1;
for(let i = 0; i < gr[v].length; i++)
{
if (gr[v][i] != par)
{
dfs(gr[v][i], v);
// Count the pair of vertices at
// distance k
for(let j = 1; j <= k; j++)
ans += d[gr[v][i]][j - 1] * d[v][k - j];
// For all levels count vertices
for(let j = 1; j <= k; j++)
d[v][j] += d[gr[v][i]][j - 1];
}
}
}
// Driver code
n = 5;
k = 2;
for(let i = 0; i < N; i++)
gr[i] = [];
// Add edges
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
// Function call
dfs(1, 0);
// Required answer
document.write(ans);
// This code is contributed by unknown2108
</script>
4
Complejidad de tiempo: O(N)
Espacio Auxiliar: O(N * 505)
Publicación traducida automáticamente
Artículo escrito por pawan_asipu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA