Dada la posición de un alfil en un tablero de ajedrez de 8 * 8 , la tarea es contar el número total de casillas que puede visitar el alfil en un solo movimiento. La posición del alfil se indica mediante el número de fila y columna del tablero de ajedrez.
Ejemplos:
Entrada: Fila = 4, Columna = 4
Salida: 13
Entrada: Fila = 1, Columna = 1
Salida: 7
Aproximación: en el juego de ajedrez, un alfil solo puede moverse en diagonal y no hay restricción de distancia para cada movimiento.
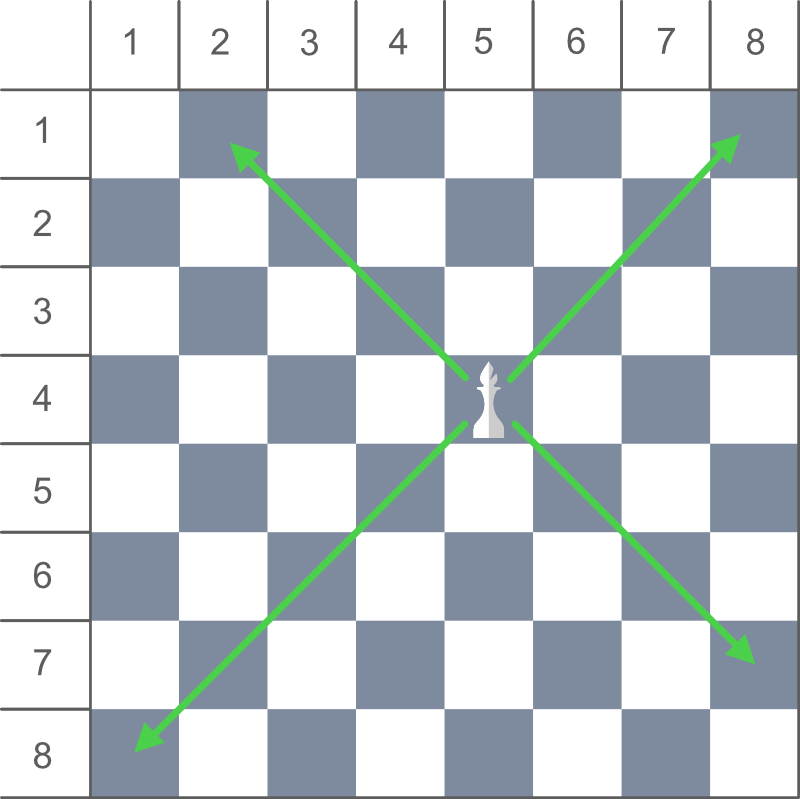
Por lo tanto, también podemos decir que Bishop puede moverse de cuatro maneras, es decir, en diagonal arriba a la izquierda, arriba a la derecha, abajo a la izquierda y abajo a la derecha desde la posición actual.
Podemos calcular el número de casillas visitadas en cada jugada por:
Total de cuadrados visitados en el movimiento superior izquierdo = min(r, c) – 1
Total de cuadrados visitados en el movimiento superior derecho = min(r, 9 – c) – 1
Total de cuadrados visitados en el movimiento inferior izquierdo = 8 – max(r, 9 – c)
Total de casillas visitadas en el movimiento inferior derecho = 8 – max(r, c)
donde, r y c son las coordenadas de la posición actual del alfil en el tablero de ajedrez.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
// Function to return the count of
// total positions the Bishop
// can visit in a single move
int countSquares(int row, int column)
{
// Count top left squares
int topLeft = min(row, column) - 1;
// Count bottom right squares
int bottomRight = 8 - max(row, column);
// Count top right squares
int topRight = min(row, 9 - column) - 1;
// Count bottom left squares
int bottomLeft = 8 - max(row, 9 - column);
// Return total count
return (topLeft + topRight + bottomRight + bottomLeft);
}
// Driver code
int main()
{
// Bishop's Position
int row = 4, column = 4;
cout << countSquares(row, column);
return 0;
}
Java
// Java implementation of above approach
class GFG {
// Function to return the count of
// total positions the Bishop
// can visit in a single move
static int countSquares(int row, int column)
{
// Count top left squares
int topLeft = Math.min(row, column) - 1;
// Count bottom right squares
int bottomRight = 8 - Math.max(row, column);
// Count top right squares
int topRight = Math.min(row, 9 - column) - 1;
// Count bottom left squares
int bottomLeft = 8 - Math.max(row, 9 - column);
// Return total count
return (topLeft + topRight + bottomRight + bottomLeft);
}
// Driver code
public static void main(String[] args)
{
// Bishop's Position
int row = 4, column = 4;
System.out.println(countSquares(row, column));
}
}
C#
// C# implementation of above approach
using System;
class GFG {
// Function to return the count of
// total positions the Bishop
// can visit in a single move
static int countSquares(int row, int column)
{
// Count top left squares
int topLeft = Math.Min(row, column) - 1;
// Count bottom right squares
int bottomRight = 8 - Math.Max(row, column);
// Count top right squares
int topRight = Math.Min(row, 9 - column) - 1;
// Count bottom left squares
int bottomLeft = 8 - Math.Max(row, 9 - column);
// Return total count
return (topLeft + topRight + bottomRight + bottomLeft);
}
// Driver code
public static void Main()
{
// Bishop's Position
int row = 4, column = 4;
Console.WriteLine(countSquares(row, column));
}
}
Python3
# Python3 implementation of above approach # Function to return the count of # total positions the Bishop # can visit in a single move def countSquares(row, column): # Count top left squares topLeft = min(row, column) - 1 # Count bottom right squares bottomRight = 8 - max(row, column) # Count top right squares topRight = min(row, 9-column) -1 # Count bottom left squares bottomLeft = 8 - max(row, 9-column) # Return total count return (topLeft + topRight + bottomRight + bottomLeft) # Driver code # Bishop's Position row = 4 column = 4 print(countSquares(row, column))
PHP
<?php
// PHP implementation of above approach
// Function to return the count of
// total positions the Bishop
// can visit in a single move
function countSquares($row, $column)
{
// Count top left squares
$topLeft = min($row, $column) - 1;
// Count bottom right squares
$bottomRight = 8 - max($row, $column);
// Count top right squares
$topRight = min($row, 9 - $column) - 1;
// Count bottom left squares
$bottomLeft = 8 - max($row, 9 - $column);
// Return total count
return ($topLeft + $topRight +
$bottomRight + $bottomLeft);
}
// Driver code
// Bishop's Position
$row = 4;
$column = 4;
echo countSquares($row, $column);
// This code is contributed by jit_t
?>
Javascript
<script>
// Javascript implementation of above approach
// Function to return the count of
// total positions the Bishop
// can visit in a single move
function countSquares(row, column)
{
// Count top left squares
var topLeft = Math.min(row, column) - 1;
// Count bottom right squares
var bottomRight = 8 - Math.max(row, column);
// Count top right squares
var topRight = Math.min(row, 9 - column) - 1;
// Count bottom left squares
var bottomLeft = 8 - Math.max(row, 9 - column);
// Return total count
return (topLeft + topRight + bottomRight + bottomLeft);
}
// Driver code
// Bishop's Position
var row = 4, column = 4;
document.write( countSquares(row, column));
</script>
13
Complejidad de tiempo: O(1)
Espacio Auxiliar: O(1)