Dada una string con alfabetos ingleses en minúsculas. La tarea es verificar si la frecuencia de los caracteres en la string se puede organizar como una serie de Fibonacci. En caso afirmativo, escriba «SI», de lo contrario escriba «NO».
Nota:
- Las frecuencias se pueden organizar de cualquier forma para formar la serie de Fibonacci.
- La serie de Fibonacci comienza desde 1. Esa es la serie es 1,1,2,3,5, …..
Ejemplos :
Input : str = "abeeedd"
Output : YES
Frequency of 'a' => 1
Frequency of 'b' => 1
Frequency of 'e' => 3
Frequency of 'd' => 2
These frequencies are first 4 terms of
Fibonacci series => {1, 1, 2, 3}
Input : str = "dzzddz"
Output : NO
Frequencies are not in Fibonacci series
Acercarse:
- Almacene las frecuencias de cada carácter de la string en un mapa. Deje que el tamaño del mapa sea
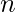 después de almacenar frecuencias.
después de almacenar frecuencias. - Luego, haz un vector e inserta los primeros ‘n’ elementos de la serie de Fibonacci en este vector.
- Luego, compare cada elemento del vector con los valores del mapa. Si ambos elementos del vector y los valores del mapa son iguales, imprima ‘SÍ’, de lo contrario imprima ‘NO’.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to check whether frequency of
// characters in a string makes
// Fibonacci Sequence
#include <bits/stdc++.h>
using namespace std;
// Function to check if the frequencies
// are in Fibonacci series
string isFibonacci(string s)
{
// map to store the
// frequencies of character
map<char, int> m;
for (int i = 0; i < s.length(); i++) {
m[s[i]]++;
}
// Vector to store first n
// fibonacci numbers
vector<int> v;
// Get the size of the map
int n = m.size();
// a and b are first and second terms of
// fibonacci series
int a = 1, b = 1;
int c;
v.push_back(a);
v.push_back(b);
// vector v contains elements of fibonacci series
for (int i = 0; i < n - 2; i++) {
v.push_back(a + b);
c = a + b;
a = b;
b = c;
}
int flag = 1;
int i = 0;
// Compare vector elements with values in Map
for (auto itr = m.begin(); itr != m.end(); itr++) {
if (itr->second != v[i]) {
flag = 0;
break;
}
i++;
}
if (flag == 1)
return "YES";
else
return "NO";
}
// Driver code
int main()
{
string s = "abeeedd";
cout << isFibonacci(s);
return 0;
}
Java
// Java program to check whether frequency of
// characters in a string makes
// Fibonacci Sequence
import java.util.HashMap;
import java.util.Vector;
class GFG
{
// Function to check if the frequencies
// are in Fibonacci series
static String isFibonacci(String s)
{
// map to store the
// frequencies of character
HashMap<Character,
Integer> m = new HashMap<>();
for (int i = 0; i < s.length(); i++)
m.put(s.charAt(i),
m.get(s.charAt(i)) == null ? 1 :
m.get(s.charAt(i)) + 1);
// Vector to store first n
// fibonacci numbers
Vector<Integer> v = new Vector<>();
// Get the size of the map
int n = m.size();
// a and b are first and second terms of
// fibonacci series
int a = 1, b = 1;
int c;
v.add(a);
v.add(b);
// vector v contains elements of
// fibonacci series
for (int i = 0; i < n - 2; i++)
{
v.add(a + b);
c = a + b;
a = b;
b = c;
}
int flag = 1;
int i = 0;
// Compare vector elements with values in Map
for (HashMap.Entry<Character,
Integer> entry : m.entrySet())
{
if (entry.getValue() != v.elementAt(i))
{
flag = 1;
break;
}
i++;
}
if (flag == 1)
return "YES";
else
return "NO";
}
// Driver Code
public static void main(String[] args)
{
String s = "abeeedd";
System.out.println(isFibonacci(s));
}
}
// This code is contributed by
// sanjeev2552
Python3
# Python3 program to check whether the frequency # of characters in a string make Fibonacci Sequence from collections import defaultdict # Function to check if the frequencies # are in Fibonacci series def isFibonacci(s): # map to store the frequencies of character m = defaultdict(lambda:0) for i in range(0, len(s)): m[s[i]] += 1 # Vector to store first n fibonacci numbers v = [] # Get the size of the map n = len(m) # a and b are first and second # terms of fibonacci series a = b = 1 v.append(a) v.append(b) # vector v contains elements of # fibonacci series for i in range(0, n - 2): v.append(a + b) c = a + b a, b = b, c flag, i = 1, 0 # Compare vector elements with values in Map for itr in sorted(m): if m[itr] != v[i]: flag = 0 break i += 1 if flag == 1: return "YES" else: return "NO" # Driver code if __name__ == "__main__": s = "abeeedd" print(isFibonacci(s)) # This code is contributed by Rituraj Jain
C#
// C# program to check whether frequency of
// characters in a string makes
// Fibonacci Sequence
using System;
using System.Collections.Generic;
class GFG
{
// Function to check if the frequencies
// are in Fibonacci series
static String isFibonacci(String s)
{
// map to store the
// frequencies of character
int i = 0;
Dictionary<int,
int> mp = new Dictionary<int,
int>();
for (i = 0; i < s.Length; i++)
{
if(mp.ContainsKey(s[i]))
{
var val = mp[s[i]];
mp.Remove(s[i]);
mp.Add(s[i], val + 1);
}
else
{
mp.Add(s[i], 1);
}
}
// List to store first n
// fibonacci numbers
List<int> v = new List<int>();
// Get the size of the map
int n = mp.Count;
// a and b are first and second terms of
// fibonacci series
int a = 1, b = 1;
int c;
v.Add(a);
v.Add(b);
// vector v contains elements of
// fibonacci series
for (i = 0; i < n - 2; i++)
{
v.Add(a + b);
c = a + b;
a = b;
b = c;
}
int flag = 1;
// Compare vector elements with values in Map
foreach(KeyValuePair<int, int> entry in mp)
{
if (entry.Value != v[i])
{
flag = 1;
break;
}
i++;
}
if (flag == 1)
return "YES";
else
return "NO";
}
// Driver Code
public static void Main(String[] args)
{
String s = "abeeedd";
Console.WriteLine(isFibonacci(s));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to check whether frequency of
// characters in a string makes
// Fibonacci Sequence
// Function to check if the frequencies
// are in Fibonacci series
function isFibonacci(s)
{
// map to store the
// frequencies of character
var m = new Map();
for (var i = 0; i < s.length; i++) {
if(m.has(s[i]))
{
m.set(s[i], m.get(s[i]));
}
else
{
m.set(s[i], 1);
}
}
// Vector to store first n
// fibonacci numbers
var v = [];
// Get the size of the map
var n = m.length;
// a and b are first and second terms of
// fibonacci series
var a = 1, b = 1;
var c;
v.push(a);
v.push(b);
// vector v contains elements of fibonacci series
for (var i = 0; i < n - 2; i++) {
v.push(a + b);
c = a + b;
a = b;
b = c;
}
var flag = 1;
var i = 0;
// Compare vector elements with values in Map
m.forEach((value, key) => {
if (value != v[i]) {
flag = 0;
}
});
if (flag == 1)
return "YES";
else
return "NO";
}
// Driver code
var s = "abeeedd";
document.write( isFibonacci(s));
</script>
Producción:
YES
Complejidad de tiempo: O(n), donde n es la longitud de la string dada.
Espacio Auxiliar: O(n)
Publicación traducida automáticamente
Artículo escrito por Shashank_Sharma y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA