Nodes mínimos para colorear en un gráfico de modo que cada Node tenga un vecino coloreado

Dado un gráfico G con Nodes V y aristas E , la tarea es colorear no más que Nodes de piso (V/2) de modo que cada Node tenga al menos un Node coloreado a una distancia de como máximo 1 unidad. La distancia entre dos Nodes conectados del gráfico siempre es exactamente 1 unidad. Imprime los Nodes que necesitan ser coloreados.

Ejemplos:  

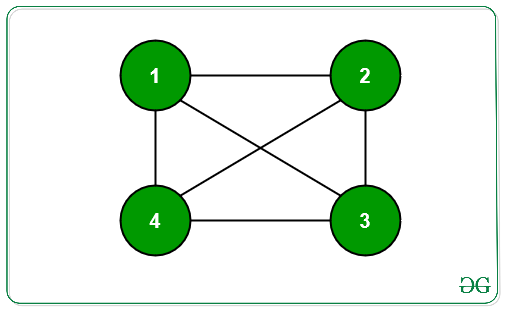
Entrada: N = 4, 
G: 
 

Salida: 1 
 

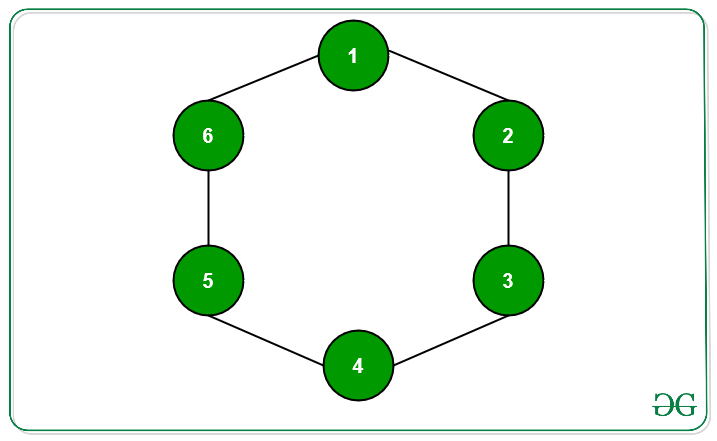
Entrada: N = 6, 
G: 
 

Salida: 3 
 

 

Enfoque: este problema se puede resolver utilizando BFS transversal. Siga los pasos a continuación para resolver el problema: 

• Inicialice las arrays impar[] e incluso[] para almacenar los Nodes que se encuentran a una distancia de un número par e impar de Nodes respectivamente de la fuente.
• A partir del Node de origen, realice un recorrido BFS con una distancia inicializada en 0, que indica la distancia desde el Node de origen. Almacene todos los Nodes en un nivel particular en impar[] o par[] según el valor de la distancia .
• Si la distancia es impar, es decir (distancia & 1) es 1, inserte ese Node en impar[]. De lo contrario, inserte en even[].
• Ahora imprima los Nodes de la array con elementos mínimos.
• Dado que el mínimo entre el recuento de Nodes a una distancia impar o una distancia par no supera el piso (V/2) , la respuesta es correcta ya que cada Node a una distancia impar está conectado a Nodes a una distancia par y viceversa.
• Por lo tanto, si el número de Nodes a la misma distancia de la fuente es menor, imprima los Nodes desde even[]. De lo contrario, imprima todos los Nodes desde impar[].

Ilustración: 
para el gráfico G que se muestra a continuación, el 
Node de origen S = 1 
 

• par[] = {1, 3, 5}
• impar[] = {2, 6, 4}
• mínimo(par.tamaño(), impar.tamaño()) = min(3, 3) = 3
• Por lo tanto, colorear todos los Nodes a una distancia impar de la fuente o incluso a una distancia de la fuente es correcto ya que ambos tienen el mismo recuento.

A continuación se muestra la implementación del enfoque anterior: 

// C++ Program to implement the
// above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Stores the graph
map<int, vector<int> > graph;
 
// Stores the visited nodes
map<int, int> vis;
 
// Stores the nodes
// at odd distance
vector<int> odd;
 
// Stores the nodes at
// even distance
vector<int> even;
 
// Function to separate and
// store the odd and even
// distant nodes from source
void bfs()
{
    // Source node
    int src = 1;
 
    // Stores the nodes and their
    // respective distances from
    // the source
    queue<pair<int, int> > q;
 
    // Insert the source
    q.push({ src, 0 });
 
    // Mark the source visited
    vis[src] = 1;
 
    while (!q.empty()) {
 
        // Extract a node from the
        // front of the queue
        int node = q.front().first;
        int dist = q.front().second;
        q.pop();
 
        // If distance from source
        // is odd
        if (dist & 1) {
            odd.push_back(node);
        }
 
        // Otherwise
        else {
            even.push_back(node);
        }
 
        // Traverse its neighbors
        for (auto i : graph[node]) {
 
            // Insert its unvisited
            // neighbours into the queue
            if (!vis.count(i)) {
 
                q.push({ i, (dist + 1) });
                vis[i] = 1;
            }
        }
    }
}
 
// Driver Program
int main()
{
    graph[1].push_back(2);
    graph[2].push_back(1);
    graph[2].push_back(3);
    graph[3].push_back(2);
    graph[3].push_back(4);
    graph[4].push_back(3);
    graph[4].push_back(5);
    graph[5].push_back(4);
    graph[5].push_back(6);
    graph[6].push_back(5);
    graph[6].push_back(1);
    graph[1].push_back(6);
 
    bfs();
 
    if (odd.size() < even.size()) {
        for (int i : odd) {
            cout << i << " ";
        }
    }
    else {
        for (int i : even) {
            cout << i << " ";
        }
    }
    return 0;
}

// Java program to implement the
// above approach
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Map;
import java.util.Queue;
 
class Pair
{
    int first, second;
 
    public Pair(int first, int second)
    {
        this.first = first;
        this.second = second;
    }
}
 
class GFG{
 
// Stores the graph
static Map<Integer, ArrayList<Integer>> graph = new HashMap<>();
 
// Stores the visited nodes
static Map<Integer, Integer> vis = new HashMap<>();
 
// Stores the nodes
// at odd distance
static ArrayList<Integer> odd = new ArrayList<>();
 
// Stores the nodes at
// even distance
static ArrayList<Integer> even = new ArrayList<>();
 
// Function to separate and
// store the odd and even
// distant nodes from source
static void bfs()
{
     
    // Source node
    int src = 1;
 
    // Stores the nodes and their
    // respective distances from
    // the source
    Queue<Pair> q = new LinkedList<>();
 
    // Insert the source
    q.add(new Pair(src, 0));
 
    // Mark the source visited
    vis.put(src, 1);
 
    while (!q.isEmpty())
    {
         
        // Extract a node from the
        // front of the queue
        int node = q.peek().first;
        int dist = q.peek().second;
        q.poll();
 
        // If distance from source
        // is odd
        if ((dist & 1) != 0)
        {
            odd.add(node);
        }
 
        // Otherwise
        else
        {
            even.add(node);
        }
 
        // Traverse its neighbors
        for(Integer i : graph.get(node))
        {
             
            // Insert its unvisited
            // neighbours into the queue
            if (!vis.containsKey(i))
            {
                q.add(new Pair(i, (dist + 1)));
                vis.put(i, 1);
            }
        }
    }
}
 
// Driver code
public static void main(String[] args)
{
    graph.put(1, new ArrayList<>());
    graph.put(2, new ArrayList<>());
    graph.put(3, new ArrayList<>());
    graph.put(4, new ArrayList<>());
    graph.put(5, new ArrayList<>());
    graph.put(6, new ArrayList<>());
    graph.get(1).add(2);
    graph.get(2).add(1);
    graph.get(2).add(3);
    graph.get(3).add(2);
    graph.get(3).add(4);
    graph.get(4).add(3);
    graph.get(4).add(5);
    graph.get(5).add(4);
    graph.get(5).add(6);
    graph.get(6).add(5);
    graph.get(6).add(1);
    graph.get(1).add(6);
 
    bfs();
 
    if (odd.size() < even.size())
    {
        for(int i : odd)
        {
            System.out.print(i + " ");
        }
    }
    else
    {
        for(int i : even)
        {
            System.out.print(i + " ");
        }
    }
}
}
 
// This code is contributed by sanjeev2552

# Python3 Program to implement the
# above approach
  
# Stores the graph
graph = dict()
  
# Stores the visited nodes
vis = dict()
  
# Stores the nodes
# at odd distance
odd = []
  
# Stores the nodes at
# even distance
even = []
  
# Function to separate and
# store the odd and even
# distant nodes from source
def bfs():
 
    # Source node
    src = 1;
  
    # Stores the nodes and their
    # respective distances from
    # the source
    q = []
  
    # Insert the source
    q.append([ src, 0 ]);
  
    # Mark the source visited
    vis[src] = 1;
  
    while (len(q) != 0):
  
        # Extract a node from the
        # front of the queue
        node = q[0][0]
        dist = q[0][1]
        q.pop(0);
  
        # If distance from source
        # is odd
        if (dist & 1):
            odd.append(node);
  
        # Otherwise
        else:
            even.append(node);
          
        # Traverse its neighbors
        for i in graph[node]:
  
            # Insert its unvisited
            # neighbours into the queue
            if (i not in vis):
  
                q.append([ i, (dist + 1) ]);
                vis[i] = 1;
              
# Driver code
if __name__=='__main__':
 
    graph[1] = [2, 6]
    graph[2] = [1, 3]
    graph[3] = [2, 4]
    graph[4] = [3, 5]
    graph[5] = [4, 6]
    graph[6] = [5, 1]
  
    bfs();
  
    if (len(odd) < len(even)):
        for i in odd:
            print(i, end = ' ')
             
    else:
        for i in even:
            print(i, end = ' ')
             
# This code is contributed by rutvik_56

1 3 5

Complejidad temporal: O(V + E)
 Espacio auxiliar : O(V)