Dados dos enteros D y A que representan la distancia perpendicular desde el origen a una línea recta y el ángulo formado por la perpendicular con el eje x positivo respectivamente, la tarea es encontrar la ecuación de la línea recta.
Ejemplos:
Entrada: D = 10, A = 30 grados
Salida: 0,87x +0,50y = 10Entrada: D = 12, A = 45 grados
Salida: 0,71x +0,71y = 12
Enfoque: El problema dado se puede resolver con base en las siguientes observaciones:
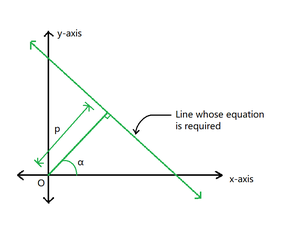
Figura 1
- Sea la distancia perpendicular (p) y el ángulo entre la perpendicular y el eje x positivo (α) grados .
- Considere un punto P con coordenadas (x, y) en la línea requerida.
- Dibuja una perpendicular desde P para encontrarse con el eje x en L .
- Desde L , dibuje una perpendicular en OQ en M.
- Ahora, dibuje una perpendicular desde P para encontrarse con ML en N .
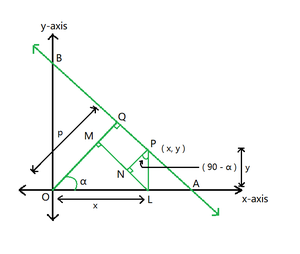
Figura 2
Ahora considere el triángulo rectángulo OLM
— (1)
Ahora considere el triángulo rectángulo PNL
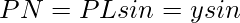
— (2)
Ahora
usando las ecuaciones (1) y (2)que es la ecuación de la línea requerida
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the approach
#include <bits/stdc++.h>
using namespace std;
// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
void findLine(int distance, float degree)
{
// Convert angle from degree to radian
float x = degree * 3.14159 / 180;
// Handle the special case
if (degree > 90) {
cout << "Not Possible";
return;
}
// Calculate the sin and cos of angle
float result_1 = sin(x);
float result_2 = cos(x);
// Print the equation of the line
cout << fixed << setprecision(2)
<< result_2 << "x +"
<< result_1 << "y = " << distance;
}
// Driver Code
int main()
{
// Given Input
int D = 10;
float A = 30;
// Function Call
findLine(D, A);
return 0;
}
Java
// Java program for the approach
class GFG{
// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
static void findLine(int distance, float degree)
{
// Convert angle from degree to radian
float x = (float) (degree * 3.14159 / 180);
// Handle the special case
if (degree > 90) {
System.out.print("Not Possible");
return;
}
// Calculate the sin and cos of angle
float result_1 = (float) Math.sin(x);
float result_2 = (float) Math.cos(x);
// Print the equation of the line
System.out.print(String.format("%.2f",result_2)+ "x +"
+ String.format("%.2f",result_1)+ "y = " + distance);
}
// Driver Code
public static void main(String[] args)
{
// Given Input
int D = 10;
float A = 30;
// Function Call
findLine(D, A);
}
}
// This code is contributed by shikhasingrajput
Python3
# Python3 program for the approach
import math
# Function to find equation of a line whose
# distance from origin and angle made by the
# perpendicular from origin with x-axis is given
def findLine(distance, degree):
# Convert angle from degree to radian
x = degree * 3.14159 / 180
# Handle the special case
if (degree > 90):
print("Not Possible")
return
# Calculate the sin and cos of angle
result_1 = math.sin(x)
result_2 = math.cos(x)
# Print the equation of the line
print('%.2f' % result_2,
"x +", '%.2f' % result_1,
"y = ", distance, sep = "")
# Driver code
# Given Input
D = 10
A = 30
# Function Call
findLine(D, A)
# This code is contributed by mukesh07
C#
// C# program for the approach
using System;
class GFG
{
// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
static void findLine(int distance, float degree)
{
// Convert angle from degree to radian
float x = (float)(degree * 3.14159 / 180);
// Handle the special case
if (degree > 90) {
Console.WriteLine("Not Possible");
return;
}
// Calculate the sin and cos of angle
float result_1 = (float)(Math.Sin(x));
float result_2 = (float)(Math.Cos(x));
// Print the equation of the line
Console.WriteLine(result_2.ToString("0.00") + "x +"
+ result_1.ToString("0.00") + "y = " + distance);
}
static void Main ()
{
// Given Input
int D = 10;
float A = 30;
// Function Call
findLine(D, A);
}
}
// This code is contributed by suresh07.
Javascript
<script>
// JavaScript program for the above approach
// Function to find equation of a line whose
// distance from origin and angle made by the
// perpendicular from origin with x-axis is given
function findLine(distance, degree) {
// Convert angle from degree to radian
let x = degree * 3.14159 / 180;
// Handle the special case
if (degree > 90) {
document.write("Not Possible");
return;
}
// Calculate the sin and cos of angle
let result_1 = Math.sin(x);
let result_2 = Math.cos(x);
// Print the equation of the line
document.write(result_2.toPrecision(2) + "x + "
+ result_1.toPrecision(2) + "y = " + distance);
}
// Driver Code
// Given Input
let D = 10;
let A = 30;
// Function Call
findLine(D, A);
// This code is contributed by Hritik
</script>
0.87x +0.50y = 10
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por arjundevmishra6 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA